数模-微分方程（种群相互依存模型）

模型

代码

fun1.m

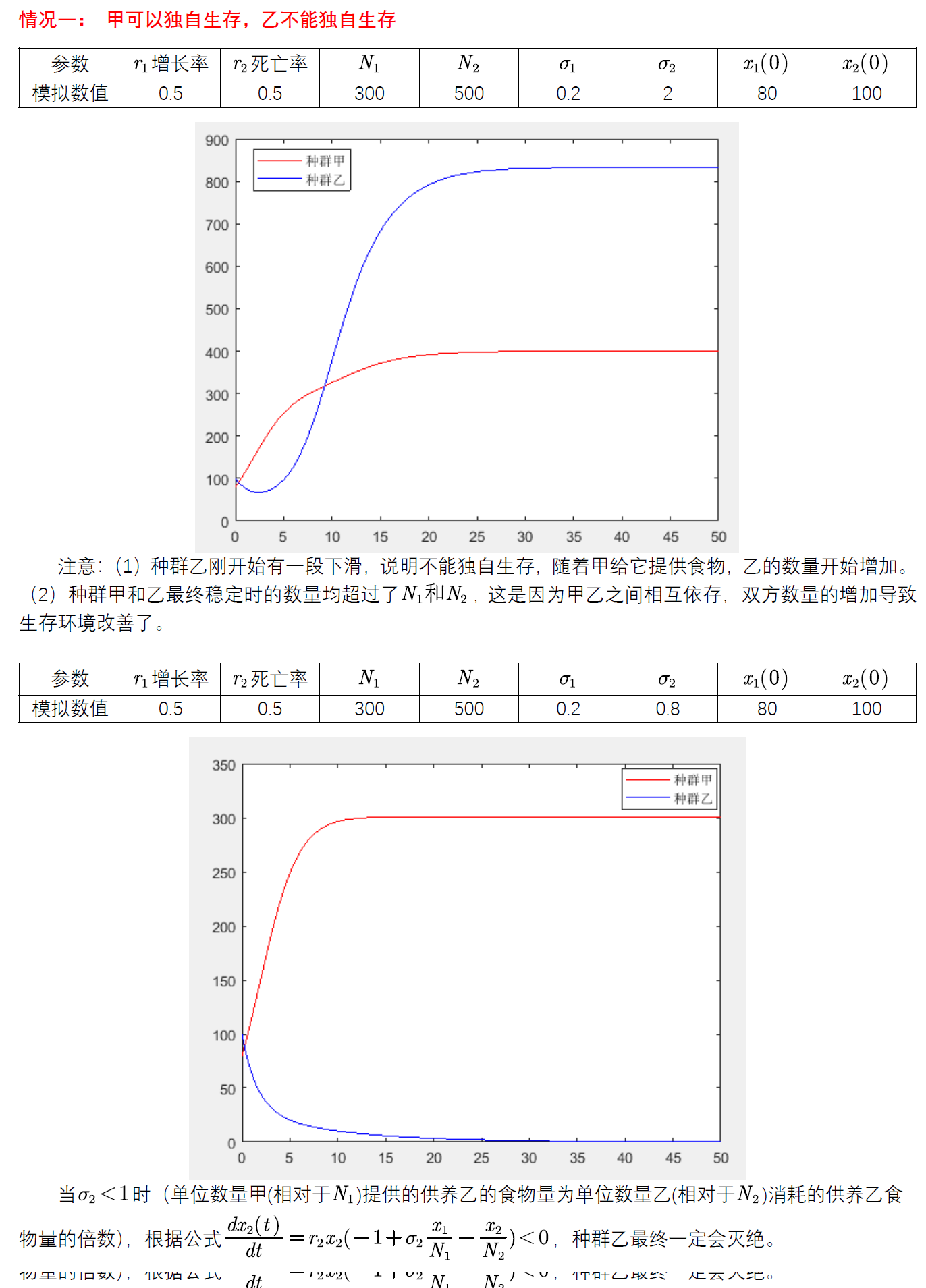
% 情况一：甲可以独自生存，乙不能独自生存
function dx=fun1(t,x)   % 大家可以修改里面的参数，来看结果的变化
    r1=0.5;  r2=0.5; % 甲的增长率和乙的死亡率
    N1=300;   N2=500;   % 甲乙的最大数量
    % sigma1: 单位数量的乙种群(相对于N2)提供的供养甲的食物量为单位数量的甲(相对于N1)消耗的供养甲的食物量的倍数。
    % sigma2: 单位数量的甲种群(相对于N1)提供的供养乙的食物量为单位数量的乙(相对于N2)消耗的供养乙的食物量的倍数。
    sigma1=0.2;  sigma2=2;   
%     sigma1=0.2;  sigma2=0.8;
% 注意：当sigma1*sigma2>1时，微分方程不稳定，matlab计算数值解时可能会报错，这时候需要调整计算的范围。
%     sigma1=3;  sigma2=3;   
    dx = zeros(2,1);
    dx(1) = r1*x(1)*(1-x(1)/N1+sigma1*x(2)/N2);
    dx(2) = r2*x(2)*(-1-x(2)/N2+sigma2*x(1)/N1);
end

fun2.m

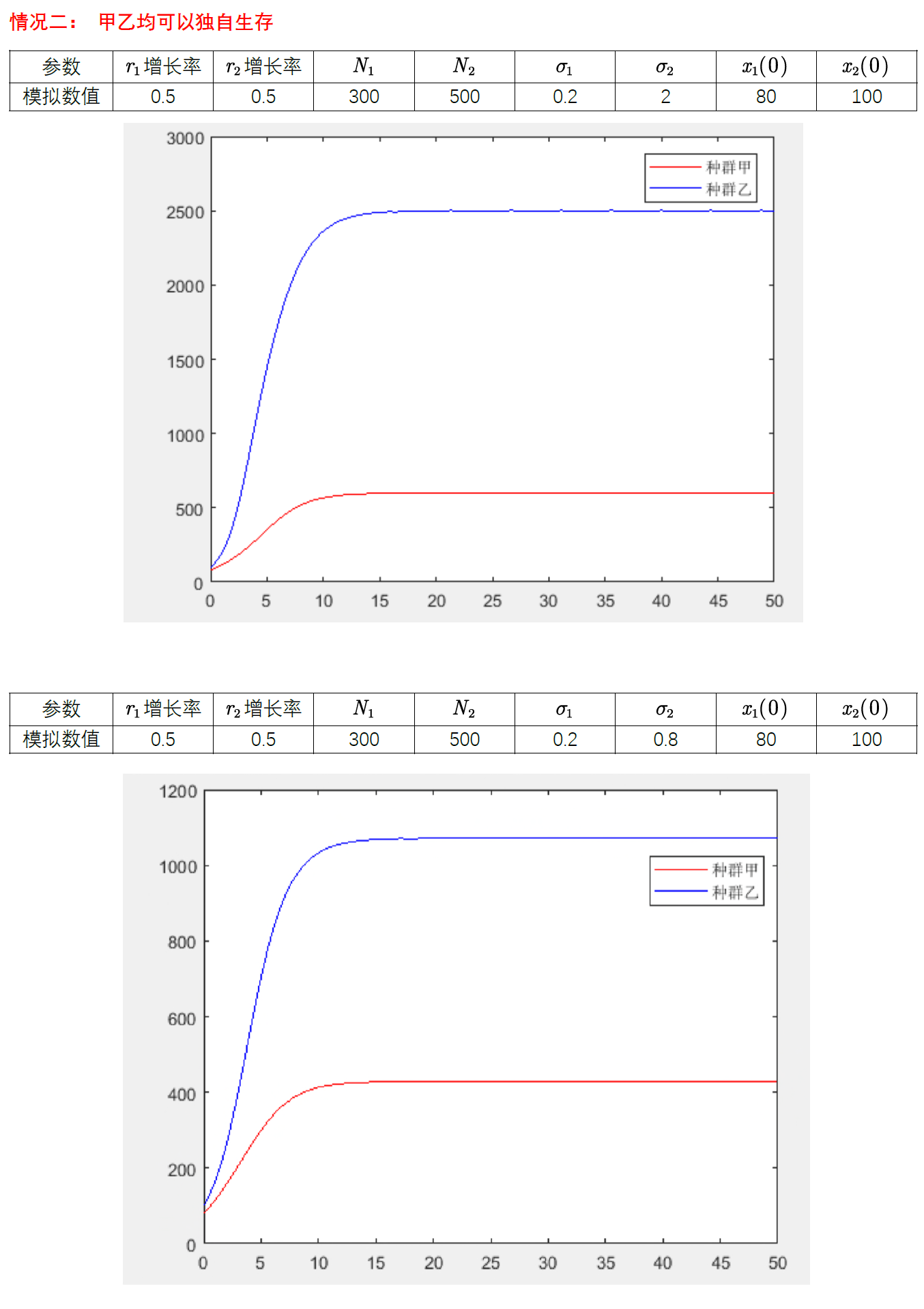
% 情况二：甲乙均可以独自生存
function dx=fun2(t,x)   % 大家可以修改里面的参数，来看结果的变化
    r1=0.5;  r2=0.5; % 甲的增长率和乙的增长率
    N1=300;   N2=500;   % 甲乙的最大数量
    % sigma1: 单位数量的乙种群(相对于N2)提供的供养甲的食物量为单位数量的甲(相对于N1)消耗的供养甲的食物量的倍数。
    % sigma2: 单位数量的甲种群(相对于N1)提供的供养乙的食物量为单位数量的乙(相对于N2)消耗的供养乙的食物量的倍数。
    sigma1=0.2;  sigma2=2;   
%     sigma1=0.2;  sigma2=0.8;
    % 注意：当sigma1*sigma2>1时，微分方程不稳定，matlab计算数值解时可能会报错。
    dx = zeros(2,1);
    dx(1) = r1*x(1)*(1-x(1)/N1+sigma1*x(2)/N2);
    dx(2) = r2*x(2)*(1-x(2)/N2+sigma2*x(1)/N1);
end

fun3.m

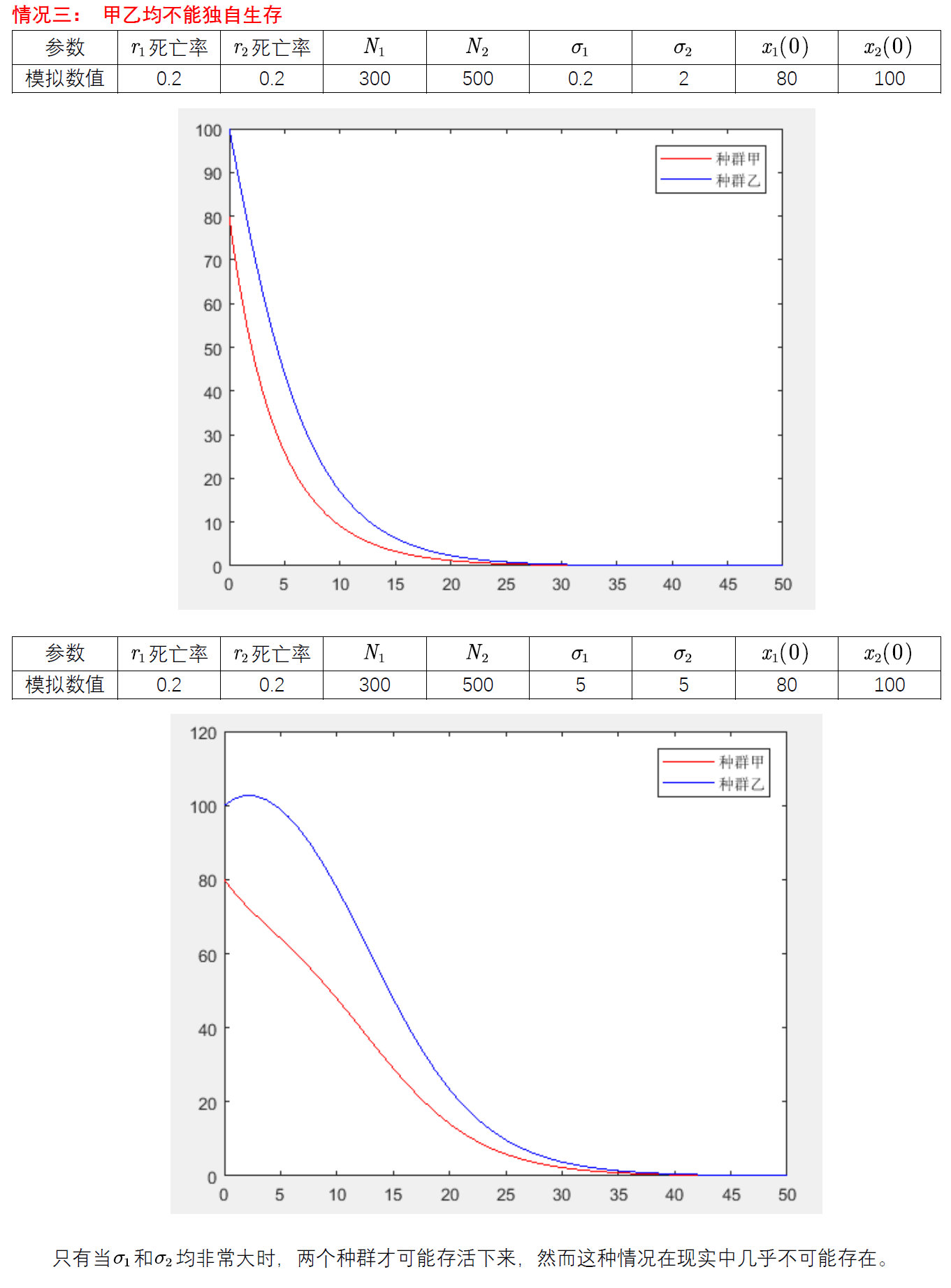
% 情况三：甲乙均不能独自生存
function dx=fun3(t,x)   % 大家可以修改里面的参数，来看结果的变化
    r1=0.2;  r2=0.2; % 甲的死亡率和乙的死亡率
    N1=300;   N2=500;    % 甲乙的最大数量
    % sigma1: 单位数量的乙种群(相对于N2)提供的供养甲的食物量为单位数量的甲(相对于N1)消耗的供养甲的食物量的倍数。
    % sigma2: 单位数量的甲种群(相对于N1)提供的供养乙的食物量为单位数量的乙(相对于N2)消耗的供养乙的食物量的倍数。
    sigma1=0.2;  sigma2=2;   
%     sigma1=5;  sigma2=5; 
%     sigma1=10;  sigma2=10;  % 这时候甲乙两个种群都能活下去了 
    dx = zeros(2,1);
    dx(1) = r1*x(1)*(-1-x(1)/N1+sigma1*x(2)/N2);
    dx(2) = r2*x(2)*(-1-x(2)/N2+sigma2*x(1)/N1);
end

code.m

clc;clear
% 情况一：甲可以独自生存，乙不能独自生存
[t,x]=ode45('fun1',[0 50],[80 100]); 
figure(1)
plot(t,x(:,1),'r-',t,x(:,2),'b-')  % x的第一列是甲种群数量，x的第二列是乙种群数量
legend('种群甲','种群乙')

% 情况二：甲乙均可以独自生存
[t,x]=ode45('fun2',[0 50],[80 100]); 
figure(2)
plot(t,x(:,1),'r-',t,x(:,2),'b-')  % x的第一列是甲种群数量，x的第二列是乙种群数量
legend('种群甲','种群乙')

% 情况三：甲乙均不能独自生存
[t,x]=ode45('fun3',[0 50],[80 100]); 
figure(3)
plot(t,x(:,1),'r-',t,x(:,2),'b-')  % x的第一列是甲种群数量，x的第二列是乙种群数量
legend('种群甲','种群乙')

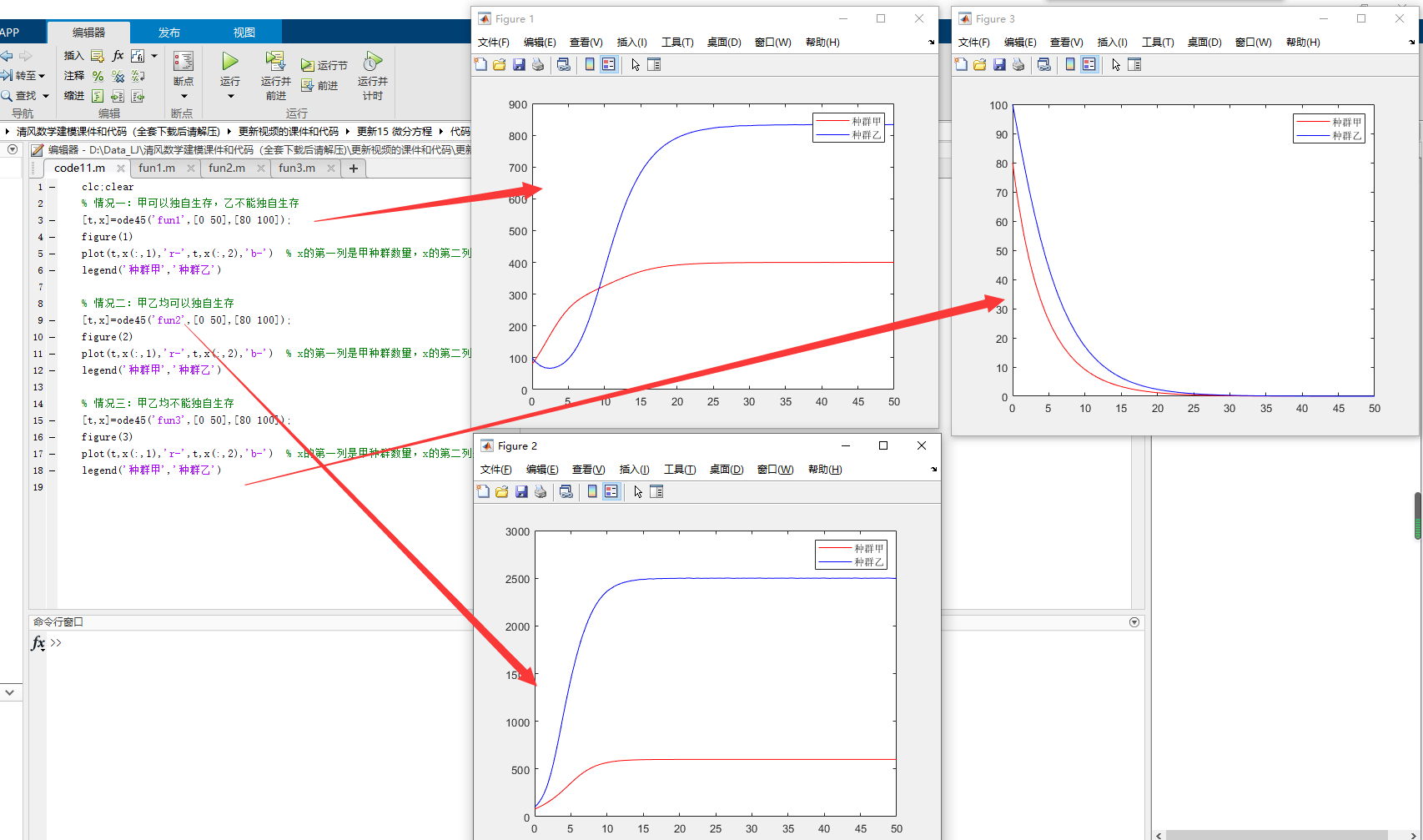
结果