数模-微分方程（MATLAB求微分方程数值解、导弹追踪问题）

小技巧：MATLAB鼠标放在变量上面能够显示数值

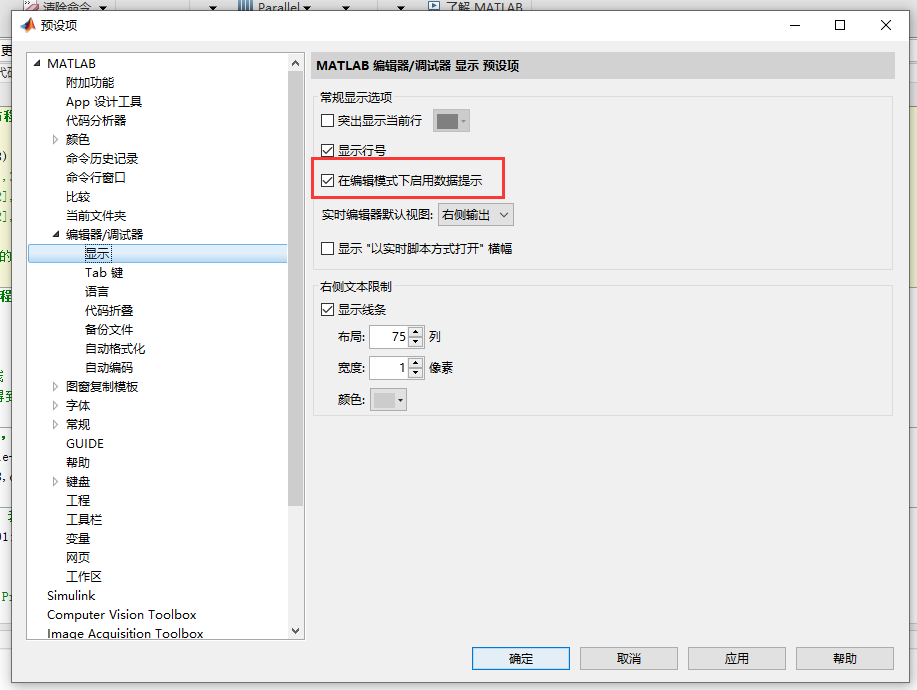
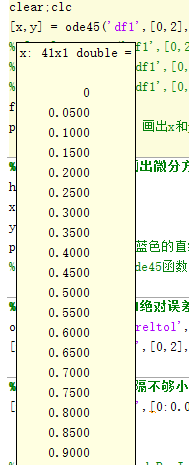
这样就能显示啦

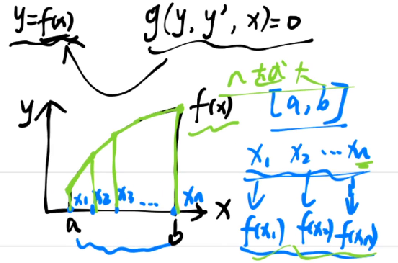
Matlab求一阶微分方程数值解

数值解就是求一个一个点的值，然后连接在一起

例一

df1.m

function dy = df1(x,y)
    % 微分方程：y-y'=2x（函数名称可以任意取）
    dy = y - 2*x; % 写成标准形式 y' = y - 2x 
    % 注意函数的返回值一定是因变量y的一阶导数
    % 函数的输入有两个，分别是自变量x和因变量y
end

code.m

%% 调用ode45函数求解微分方程df1，自变量为x，范围为[0,2],  初始值y(0)=3 ; 因变量为y
clear;clc
[x,y] = ode45('df1',[0,2],3);  % [x,y] = ode45(@df1,[0,2],3);
% [x,y] = ode23('df1',[0,2],3);
% [x,y] = ode113('df1',[0,2],3);
% [x,y] = ode15s('df1',[0,2],3); % 刚性
figure(1)
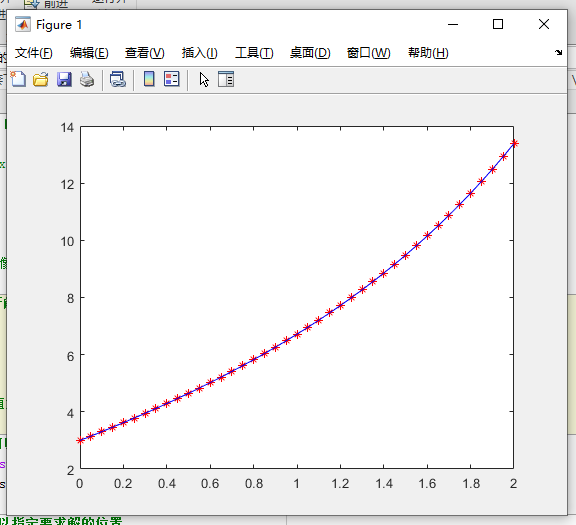
plot(x,y,'r*-')  % 画出x和y的函数图像，用红色的直线和*标记

%%  下面我们直接画出微分方程的解析解的图像进行对比
hold on
x = 0:0.01:2;
y = exp(x)+2*x+2;
plot(x,y,'b-')  % 蓝色的直线
% 从图中可以看出，ode45函数得到的数值解的精度很高。

%%  设定相对误差和绝对误差，这样可以提高微分方程数值解的精度
options = odeset('reltol',1e-4,'abstol',1e-8);
[x,y] = ode45('df1',[0,2],3,options);

%%  如果觉得x的间隔不够小，我们可以指定要求解的位置
[x,y] = ode45('df1',[0:0.001:2],3,options);


% Dormand, J. R. and P. J. Prince, “A family of embedded Runge-Kutta formulae,” J. Comp. Appl. Math., Vol. 6, 1980, pp. 19–26.

解析解和数值解的图像

例二

df2.m

function dy = df2(x,y) 
       % 注意哦，x是自变量，y是因变量，由y1,y2,y3组成 
       dy = zeros(3,1);  % 初始化用来储存因变量一阶导数的列向量（不能写成行向量哦）
       dy(1) = y(2) * y(3);
       dy(2) = -y(1) * y(3);
       dy(3) = -0.51 * y(1) * y(2);
%     上面四行可以写成一行：   dy = [ y(2) * y(3);   -y(1) * y(3);  -0.51 * y(1) * y(2)]
end

code.m

%% 在真正比赛中，我们往往会倾向于先去看有无解析解，如果没有解析解再考虑数值解
% [y1 y2 y3] = dsolve('Dy1=y2*y3','Dy2=-y1*y3','Dy3=-0.51*y1*y2','y1(0)=0,y2(0)=1,y3(0)=1','x')

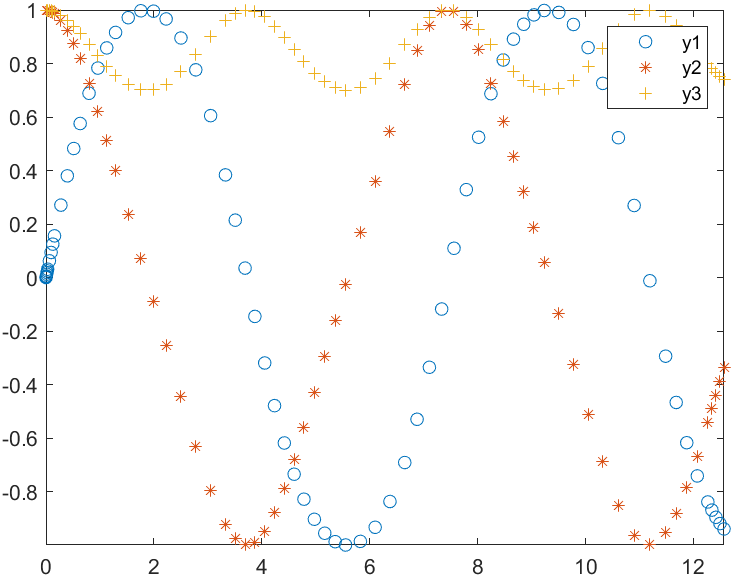
%% 调用ode45函数求解微分方程df2，自变量为x，范围为[0,4*pi] ; 因变量为y1,y2和y3，初始值: y1(0)=0,y2(0)=y3(0)=1 
[x, y] = ode45('df2', [0 4*pi], [0 1 1]);  % 这里的y是一个有3列的矩阵哦！
plot(x, y(:,1), 'o', x, y(:,2), '*', x, y(:,3), '+') 
legend('y1','y2','y3')  % 加上标注
axis([0, 4*pi, -inf, +inf])  % 设置横坐标范围为0-4pi，纵坐标范围不需要设置，写成-inf到+inf

Matlab求高阶微分方程数值解

龙格库塔方法介绍

例三

df3.m

function dy=df3(x,y) 
       dy=zeros(2,1);  % 初始化用来储存因变量一阶导数的矩阵
       dy(1)=y(2);
       dy(2)=(2*x)/(1+x*x)*y(2);
end

code.m

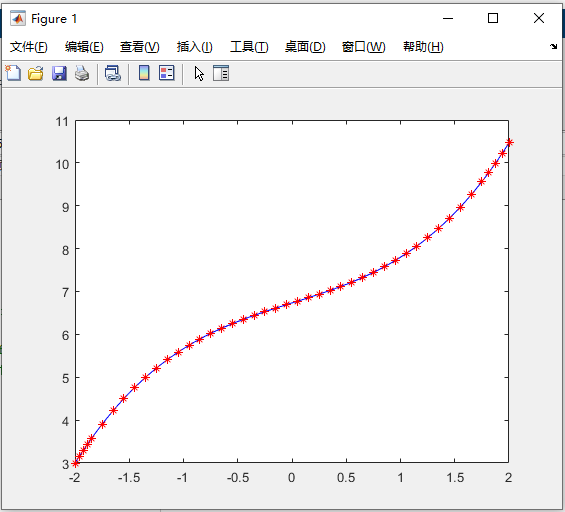
% 我们先看这个微分方程有没有解析解
dsolve('(1+x*x)*D2y=2*x*Dy','y(-2)=3,Dy(-2)=4','x')
x = -2:0.01:2;
y = (4*x.*(x.^2 + 3))/15 + 101/15;
plot(x,y,'b-')
% 事实上有了解析解后我们就完全不需要数值解了，下面我们只是为了演示怎么进行求解~
hold on % 继续在上面作图
[x,y]=ode45('df3',[-2,2],[3,4]);  % 求出这个微分方程df3的数值解
plot(x,y(:,1),'r*') % 注意，y变量有两列，第一列是y1(我们要求的y)，第二列是y2(y的一阶导数) 

解析解和数值解的图像

三阶微分方程怎么转换

要是MATLAB正忙的时候怎么终止

Ctrl+C

例4（刚性问题）

df4.m

function dy=df4(x,y)
    dy=zeros(2,1);
    dy(1)=y(2);
    dy(2)=1000*(1-y(1)^2)*y(2)-y(1);
end

code.m

% 我们先看这个微分方程有没有解析解
dsolve('D2y=1000*(1-y^2)*Dy-y','y(0)=2,Dy(0)=0','x')  % 警告: Explicit solution could not be found. 

% 下面计算数值解
% 如果使用ode45函数会发现计算的非常慢，matlab一直显示正忙(windows电脑在命令行窗口按Ctrl+C可以终止运行)
% [x,y]=ode45('df4',[0,3000],[2,0]);  % 求出这个微分方程df4的数值解
% 所以我们可以使用刚性问题的函数ode15s对其求解
[x,y]=ode15s('df4',[0,3000],[2,0]);  % 求出这个微分方程df4的数值解
plot(x,y(:,1),'*') % 注意，y变量有两列，第一列是y1(我们要求的y)，第二列是y2(y的一阶导数)

Matlab求解导弹追踪问题

df5.m

function dy=df5(t,y)
    v = 200; 
    dy=zeros(2,1);
    dy(1)=3*v*(20+sqrt(2)/2*v*t-y(1))/sqrt((20+sqrt(2)/2*v*t-y(1))^2+(sqrt(2)/2*v*t-y(2))^2);
    dy(2)=3*v*(sqrt(2)/2*v*t-y(2))/sqrt((20+sqrt(2)/2*v*t-y(1))^2+(sqrt(2)/2*v*t-y(2))^2);
end

code.m

clear; clc
options = odeset('reltol',1e-4,'abstol',1e-8);  %  设定相对误差和绝对误差，这样可以提高微分方程数值解的精度
% 下面的[0,0.1]表示时间t的范围，因为我们导弹速度假设的是200，所以这里的范围给小点
[t,y]=ode45('df5' ,[0,0.1],[0 0], options); % y是因变量，第一列为导弹运行的横坐标，第二列为导弹运行的纵坐标
% [t,y]=ode45('df5' ,[0:0.0001:0.1],[0 0], options); % y是因变量，第一列为导弹运行的横坐标，第二列为导弹运行的纵坐标
x = y(:,1);  y =y(:,2);
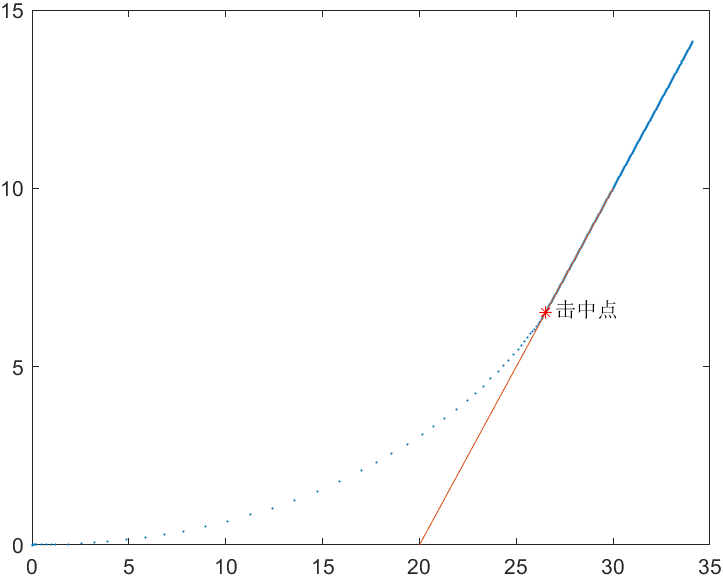
plot(x, y,'*','MarkerSize',1)  % 画出导弹的运行轨迹
hold on
plot([20,30],[0,10]) % 画出B船的运行轨迹: x-y-20=0
hold on
% 下面我们找到导弹与B船相撞的点（由于Matlab浮点数计算的原因，距离足够近时即可认为相撞）
n =length(t);  % 找到Matlab计算微分方程的数值解时一共有多少个时间点
d = 0;  % 初始化导弹飞行的距离
for i = 1:n % 开始循环
    dd = abs(x(i) - y(i) - 20) / sqrt(2);  % 利用点到直线的距离公式计算导弹和船的距离
    if dd < 0.001 % 如果这个距离足够小了，我们就认为相撞了，但再此之前别忘了判断导弹是否达到了有效射程
        for k = 2:i
            d = sqrt((x(k)-x(k-1))^2+(y(k)-y(k-1))^2) + d;  % 以直代曲的思想求曲线的长度，即导弹飞行的距离
        end
        if d <= 50 % 导弹的有效射程为50个单位,如果没有达到50单位
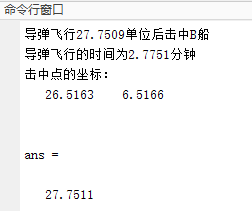
            disp(['导弹飞行',num2str(d),'单位后击中B船'])
            disp(['导弹飞行的时间为',num2str(t(i)*60 ),'分钟']) % 输出导弹击中B船的时间(转换为分钟)
            disp('击中点的坐标：');  disp([x(i),y(i)])  % 输出导弹击中B船的坐标
            plot(x(i),y(i),'r*');
            text(x(i)+0.5,y(i)+0.1,'击中点')
        end
        break; % 跳出循环
    end
end
if d >50 || dd >= 0.001 % 如果射程大于50或导弹与B船的距离始终都没有小于0.001（这个数需要根据实际情况调整）
    disp('导弹没有击中B船');
end

t(i) * 200 * 3   % 更快计算导弹飞行距离的公式：速度*时间
% 得到的结果和我们上面以直代曲的结果很接近


% 下面是以前使用蒙特卡罗模拟得到的解，大家可以对比下：
% 导弹飞行27.8019单位后击中B船
% 导弹飞行的时间为2.7802分钟
% 击中点的坐标：
%    26.5523    6.5523