数模-图论（弗洛伊德算法）

所有代码：

Floyd_algorithm.m

function [dist,path] = Floyd_algorithm(D)
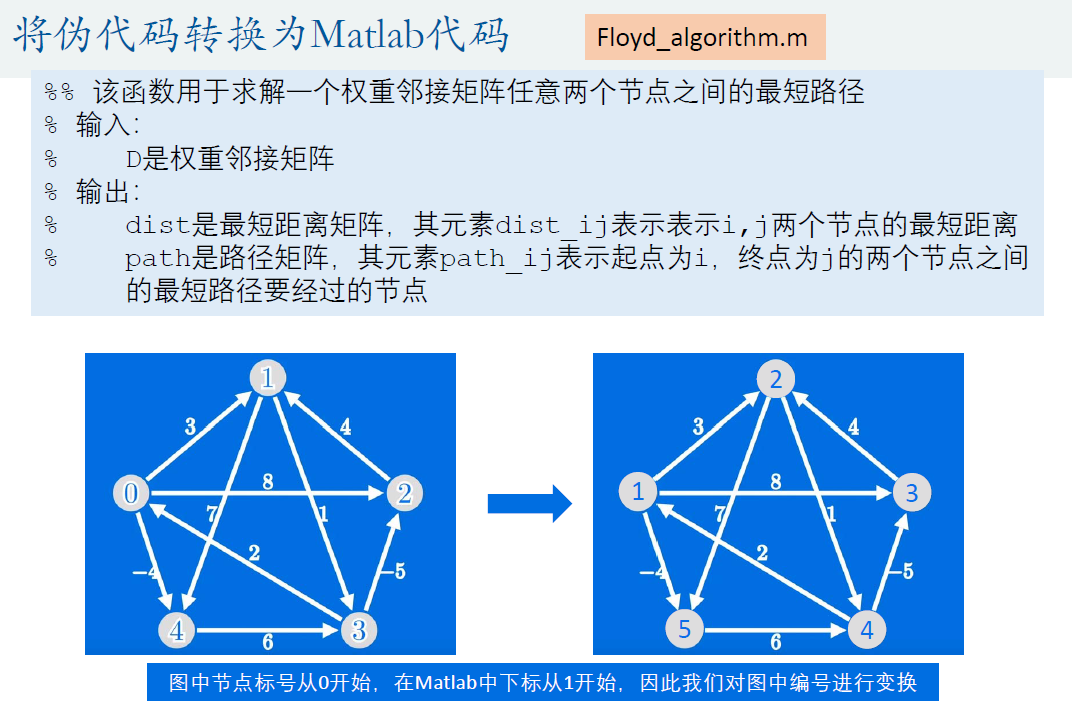
%% 该函数用于求解一个权重邻接矩阵任意两个节点之间的最短路径
% 输入：
%        D是权重邻接矩阵
% 输出：
%        dist是最短距离矩阵，其元素dist_ij表示表示i,j两个节点的最短距离
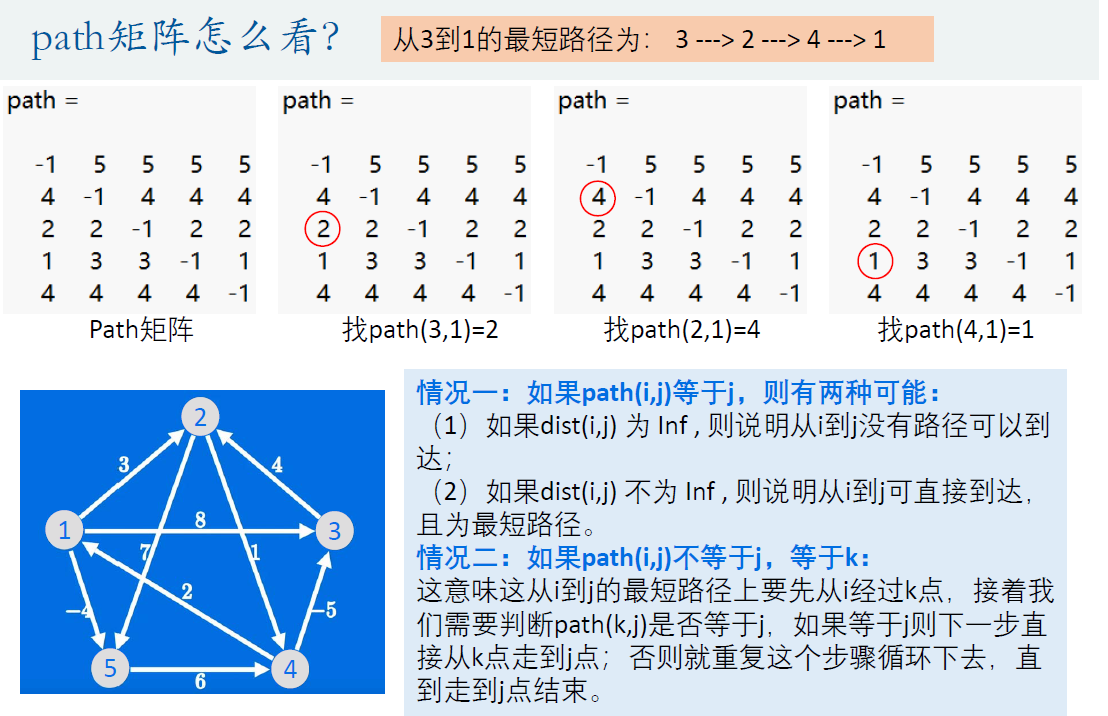
%        path是路径矩阵，其元素path_ij表示起点为i，终点为j的两个节点之间的最短路径要经过的节点

n = size(D,1);  % 计算节点的个数

% 初始化dist矩阵
dist = D;

% 下面我们来初始化path矩阵
path = zeros(n);
for j = 1:n
    path(:,j) = j;   % 将第j列的元素变为j
end
for i = 1:n
    path(i,i) = -1;  % 将主对角线元素变为-1
end

% 下面开始三个循环
for k=1:n    % 中间节点k从1- n 循环
   for i=1:n     % 起始节点i从1- n 循环
      for j=1:n    % 终点节点j从1-n 循环
          if dist(i,j)>dist(i,k)+dist(k,j)  % 如果i,j两个节点间的最短距离大于i和k的最短距离+k和j的最短距离
             dist(i,j)=dist(i,k)+dist(k,j);  % 那么我们就令这两个较短的距离之和取代i,j两点之间的最短距离
             path(i,j)=path(i,k);   % 起点为i，终点为j的两个节点之间的最短路径要经过的节点更新为path(i,k)
             % 注意，上面一行语句不能写成path(i,j) = k; 这是网上很多地方都容易犯的错误，在PPT11页中会告诉大家为什么不能这么写
          end
      end
   end
end

end

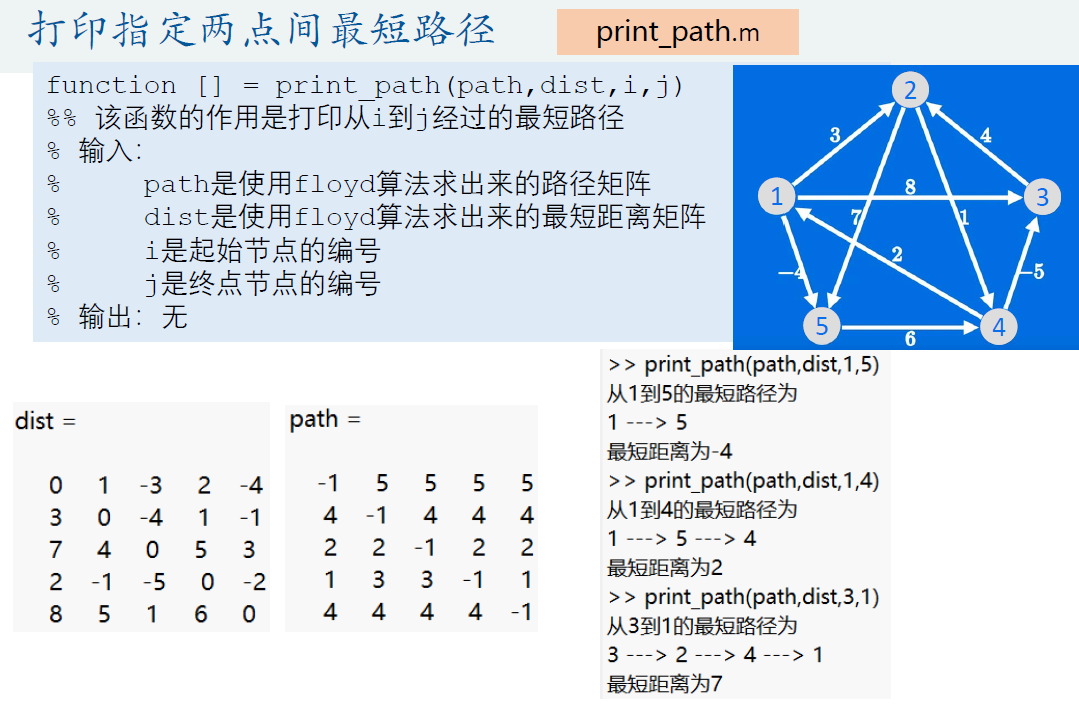
print_path.m

function [] = print_path(path,dist,i,j)
%% 该函数的作用是打印从i到j经过的最短路径
% 输入：
%        path是使用floyd算法求出来的路径矩阵
%        dist是使用floyd算法求出来的最短距离矩阵
%        i是起始节点的编号
%        j是终点节点的编号
% 输出：无

if i == j
    warning('起点和终点相同，请检查后重新输入')  % 在屏幕中提示警告信息
    return;  % 不运行下面的语句，直接退出函数
end
if path(i,j) == j   % 如果path(i,j) = j，则有两种可能：
% （1）如果dist(i,j) 为 Inf , 则说明从i到j没有路径可以到达
    if dist(i,j) == Inf
        disp(['从',num2str(i),'到',num2str(j),'没有路径可以到达'])
% （2）如果dist(i,j) 不为 Inf , 则说明从i到j可直接到达，且为最短路径
    else
        disp(['从',num2str(i),'到',num2str(j),'的最短路径为'])
        disp([num2str(i),' ---> ',num2str(j)])
        disp(['最短距离为',num2str(dist(i,j))])
    end
else  % 如果path(i,j) ~= j，则说明中间经过了其他节点：
    k = path(i,j);
    result = [num2str(i),' ---> '];  % 初始化要打印的这个字符串
    while k ~= j  % 只要k不等于j, 就一直循环下去
        result = [result , num2str(k) , ' ---> ' ];  % i先走到k这个节点处
        k = path(k,j);
    end
    result = [result , num2str(k)];
    disp(['从',num2str(i),'到',num2str(j),'的最短路径为'])
    disp(result)
    disp(['最短距离为',num2str(dist(i,j))])
end

end

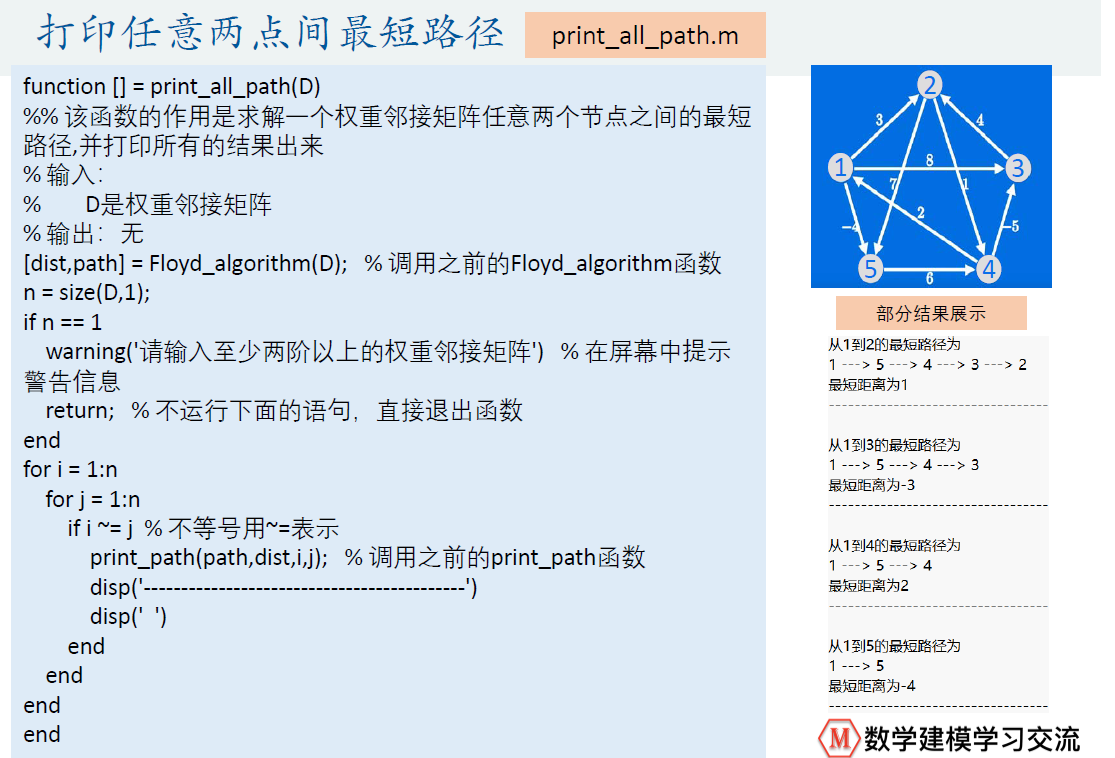
print_all_path.m

function [] = print_all_path(D)
%% 该函数的作用是求解一个权重邻接矩阵任意两个节点之间的最短路径,并打印所有的结果出来
% 输入：
%        D是权重邻接矩阵
% 输出：无

[dist,path] = Floyd_algorithm(D);   % 调用之前的Floyd_algorithm函数
n = size(D,1);
if n == 1
    warning('请输入至少两阶以上的权重邻接矩阵')   % 在屏幕中提示警告信息
    return;   % 不运行下面的语句，直接退出函数
end

for i = 1:n
    for j = 1:n
        if i ~= j  % 不等号用~=表示
            print_path(path,dist,i,j);   % 调用之前的print_path函数
            disp('-------------------------------------------')
            disp('  ')
        end
    end
end

end

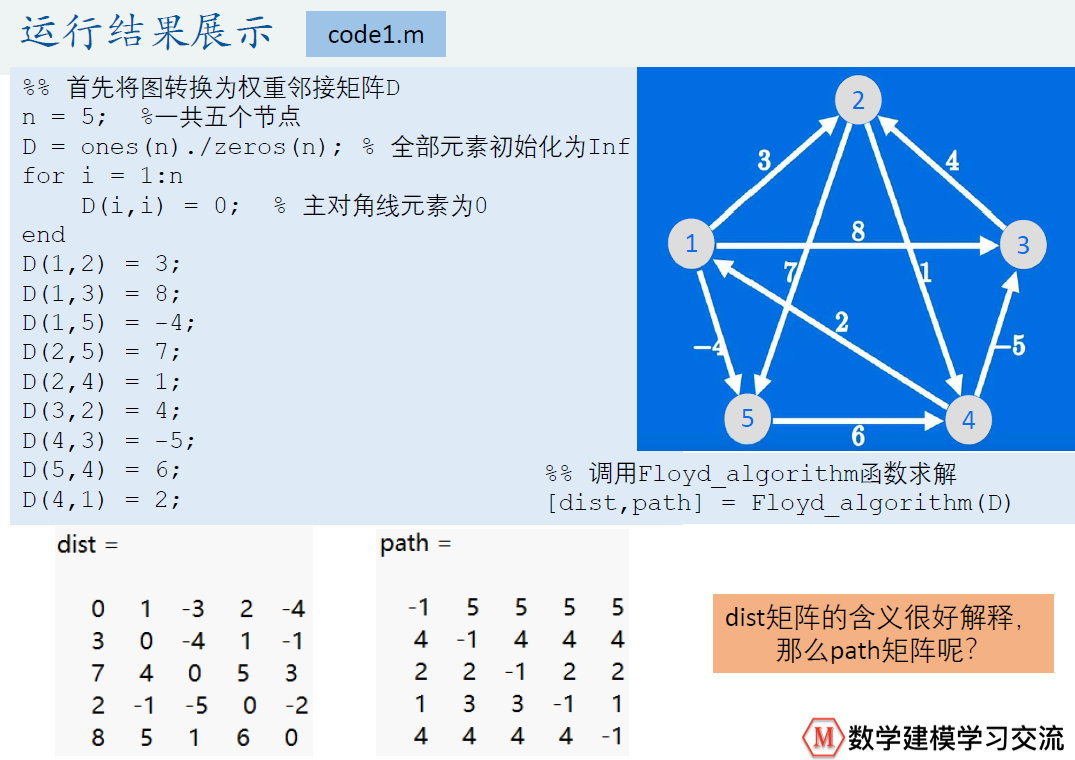
code1.m

% PPT第七页的例子
%% 首先将图转换为权重邻接矩阵D
n = 5;  %一共五个节点
D = ones(n) ./ zeros(n);  % 全部元素初始化为Inf
for i = 1:n
    D(i,i) = 0;  % 主对角线元素为0
end
D(1,2) = 3;
D(1,3) = 8;
D(1,5) = -4;
D(2,5) = 7;
D(2,4) = 1;
D(3,2) = 4;
D(4,3) = -5;
D(5,4) = 6;
D(4,1) = 2;

%% 调用Floyd_algorithm函数求解
[dist,path] = Floyd_algorithm(D)

print_path(path,dist,1,5)
print_path(path,dist,1,4)
print_path(path,dist,3,1)

clc
disp('下面我们打印任意两点之间的最短距离：')
print_all_path(D)

code2.m

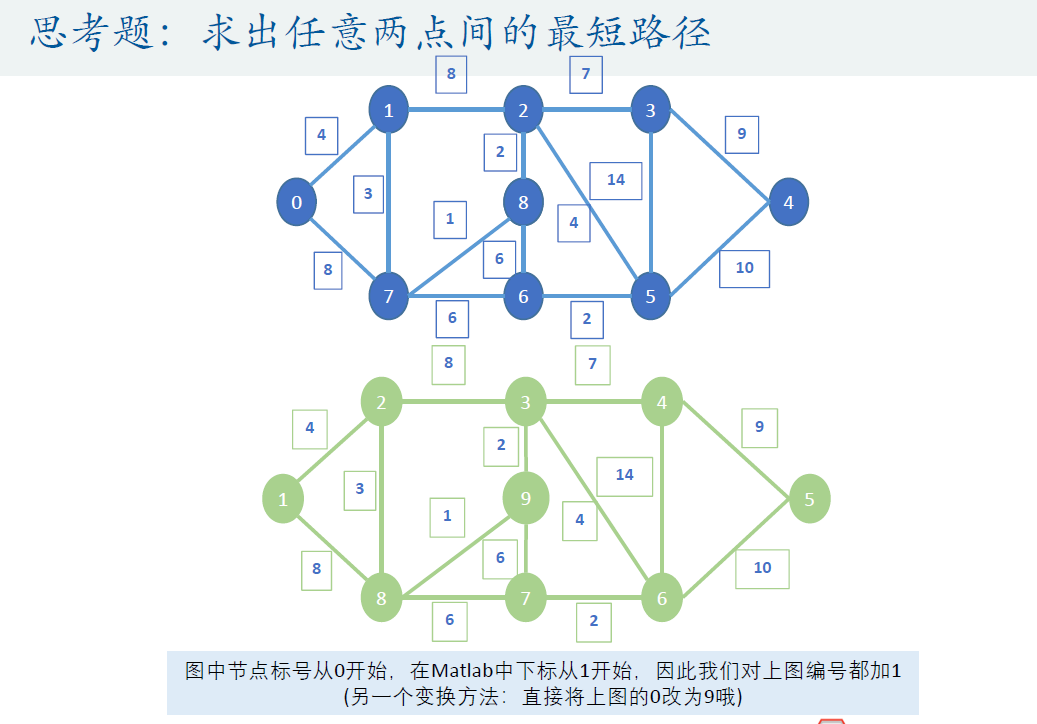
% 思考题的参考答案
%% 首先将图转换为权重邻接矩阵D
n = 9;  %一共九个节点
D = zeros(n);  % 全部元素初始化为0, 等会你们就知道为什么这样设置啦
% 因为是无向图，所以权重邻接矩阵是一个对称矩阵
D(1,2) = 4; D(1,8) = 8; 
D(2,8) = 3; D(2,3) = 8;
D(8,9) = 1; D(8,7) = 6; 
D(9,7) = 6; D(9,3) = 2;
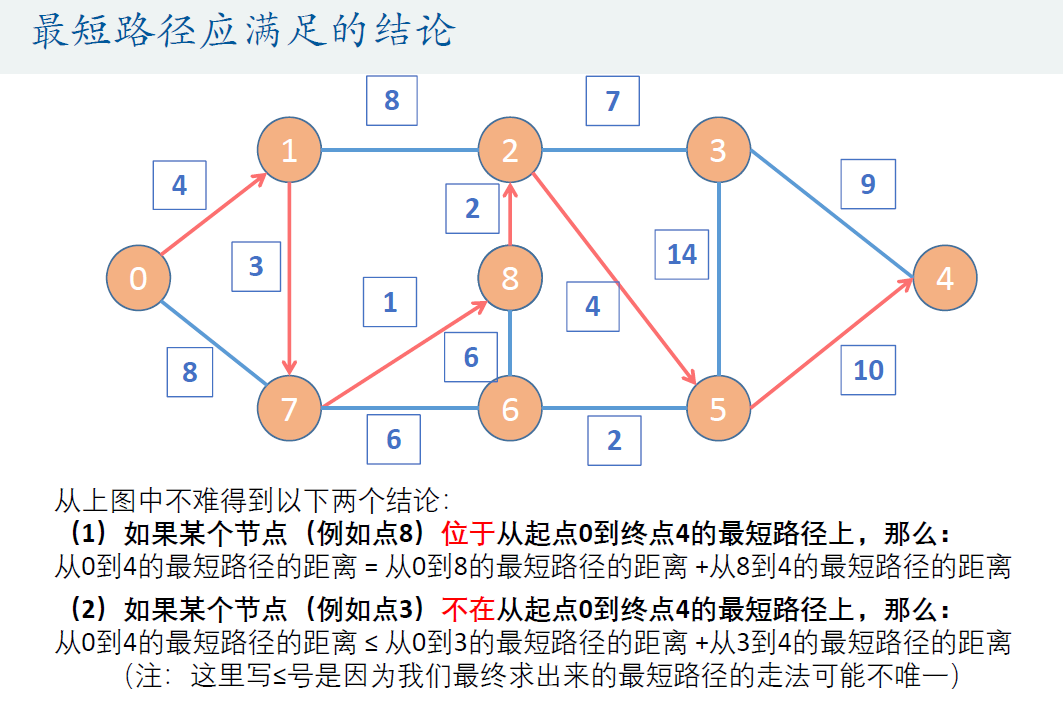
D(7,6) = 2; D(3,4) = 7; 
D(3,6) = 4; D(6,4) = 14;
D(4,5) = 9; D(6,5) = 10;
D = D+D';   % 这个操作可以得到对称矩阵的另一半
for i = 1:n
    for j = 1:n
        if (i ~= j) && (D(i,j) == 0)  
            D(i,j) = Inf;   % 将非主对角线上的0元素全部变为Inf
        end
    end
end

%% 调用Floyd_algorithm函数求解
[dist,path] = Floyd_algorithm(D)

结果：以code1为例

可以打印各点之间的最短路径

code1对应于有向图 code2对应于无向图