数模-神经网络
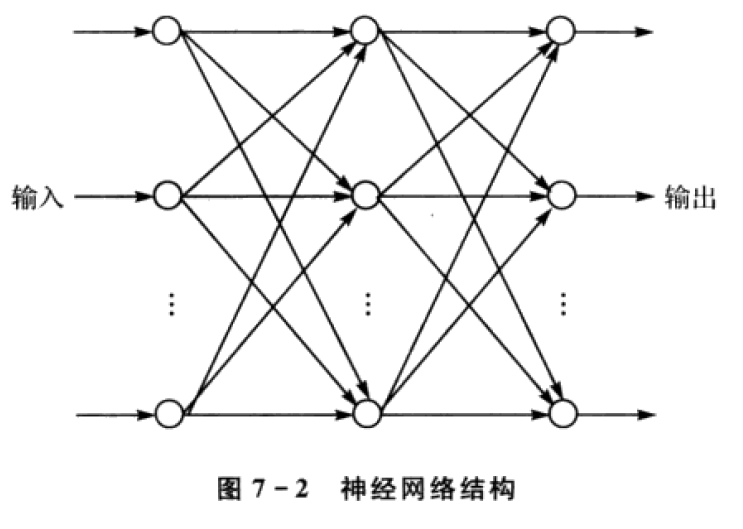
激励函数

BP网络基本数学原理


基于MATLAB工具箱的公路运量预测

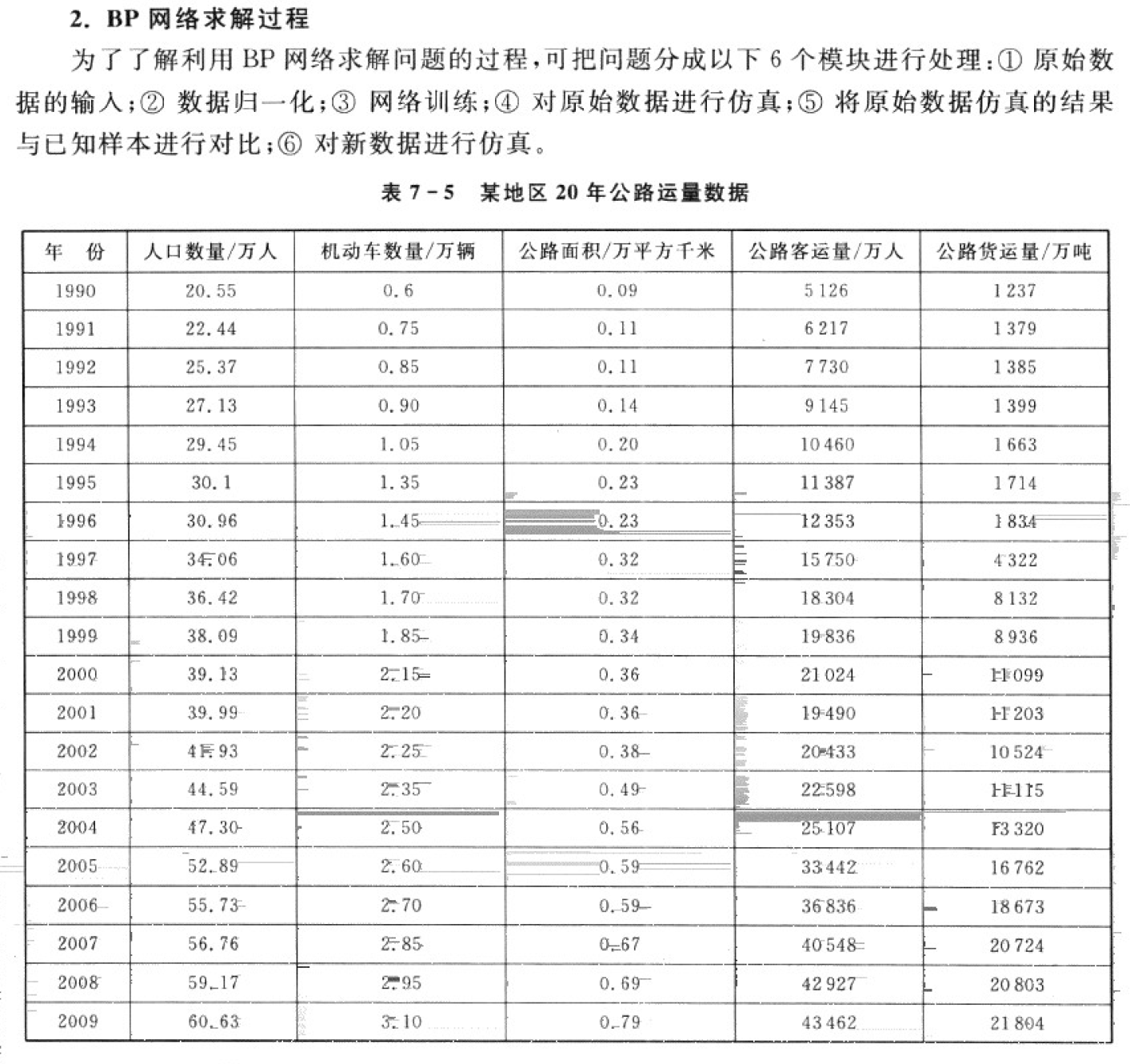
代码
clc,clear,close
%% 1.原始数据的输入
%原始数据
%人数(单位:万人)
sqrs=[20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99...
41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63];
%机动车数(单位:万辆)
sgjdcs=[0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6...
2.7 2.85 2.95 3.1];
%公路面积(单位:万平方千米)
saglmj=[0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 ...
0.56 0.59 0.59 0.67 0.69 0.79];
%公路客运量(单位:万人)
glkyl=[5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 ...
22598 25107 33442 36836 40548 42927 43462];
%公路货运量(单位:万吨)
glhyl=[1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 ...
13320 16762 18673 20724 20803 21804];
p=[sqrs;sgjdcs;saglmj];%输入数据矩阵
t=[glkyl;glhyl];%目标数据矩阵
%% 2.对输入数据矩阵和目标矩阵的数据进行归一化
%利用函数premnmx对数据进行归一化
[pn,minp,maxp,tn,mint,maxt]= premnmx(p,t);%对于输人矩阵p和输出矩阵t进行归一化处理
dx =[-1,1;-1,1;-1,1];%归一化处理后最小值为一1,最大值为1
%% 3.利用处理好的数据对网络进行训练
% BP网络训练
net = newff(dx,[3,7,2],{'tansig','tansig','purelin'},'traingdx');%建立模型,并用梯度下降法训练
net.trainParam.show=1000; %1000轮回显示一次结果
net.trainParam.Lr=0.05;%学习速率为0.05
net.trainParam.epochs =50000;%最大训练轮回为50000次
net.trainParam.goal=0.65 * 10^(-3);%均方误差
net =train(net,pn, tn);%开始训练,其中pn,tn分别为输人输出样本
%% 4.利用训练好的BP网络对原始数据进行仿真
%利用原始数据对BP网络仿真
an = sim(net, pn);%用训练好的模型进行仿真
a = postmnmx(an,mint,maxt);%把仿真得到的数据还原为原始的数量级
%% 5.用原始数据仿真的结果与已知数据进行对比测试
%本例因样本容量有限使用训练数据进行测试,通常必须用新鲜数据进行测试
x=1990:2009;
newk =a(1,:);
newh =a(2,:);
figure(2);
subplot(2,1,1);plot(x,newk,'r-o',x,glkyl,'b--+');%绘值公路客运量对比图
legend('网络输出客运量','实际客运量');
xlabel('年份');ylabel('客运量/万人');
title('运用工具箱客运量学习和测试对比图');
subplot(2,1,2);plot(x,newh,'r-o',x,glhyl,'b--+');%绘制公路货运量对比图
legend('网络输出货运量','实际货运量');
xlabel('年份');ylabel('货运量/万吨');
title('运用工具箱货运量学习和测试对比图');%利用训练好的网络进行预测
%% 利用训练好的BP网络对新数据进行仿真
%利用训练好的网络进行预测
%当用训练好的网络对新数据 pnew进行预测时,也应作相应的处理
pnew=[73.39 75.55
3.9635 4.0975
0.9880 1.0268];%2010年和2011年的相关数据
pnewn=tramnmx(pnew ,minp,maxp);%利用原始输人数据的归一化参数对新数据进行归一化
anewn = sim(net,pnewn);%利用归一化后的数据进行仿真
anew =postmnmx(anewn,mint, maxt)%把仿真得到的数据还原为原始的数量级
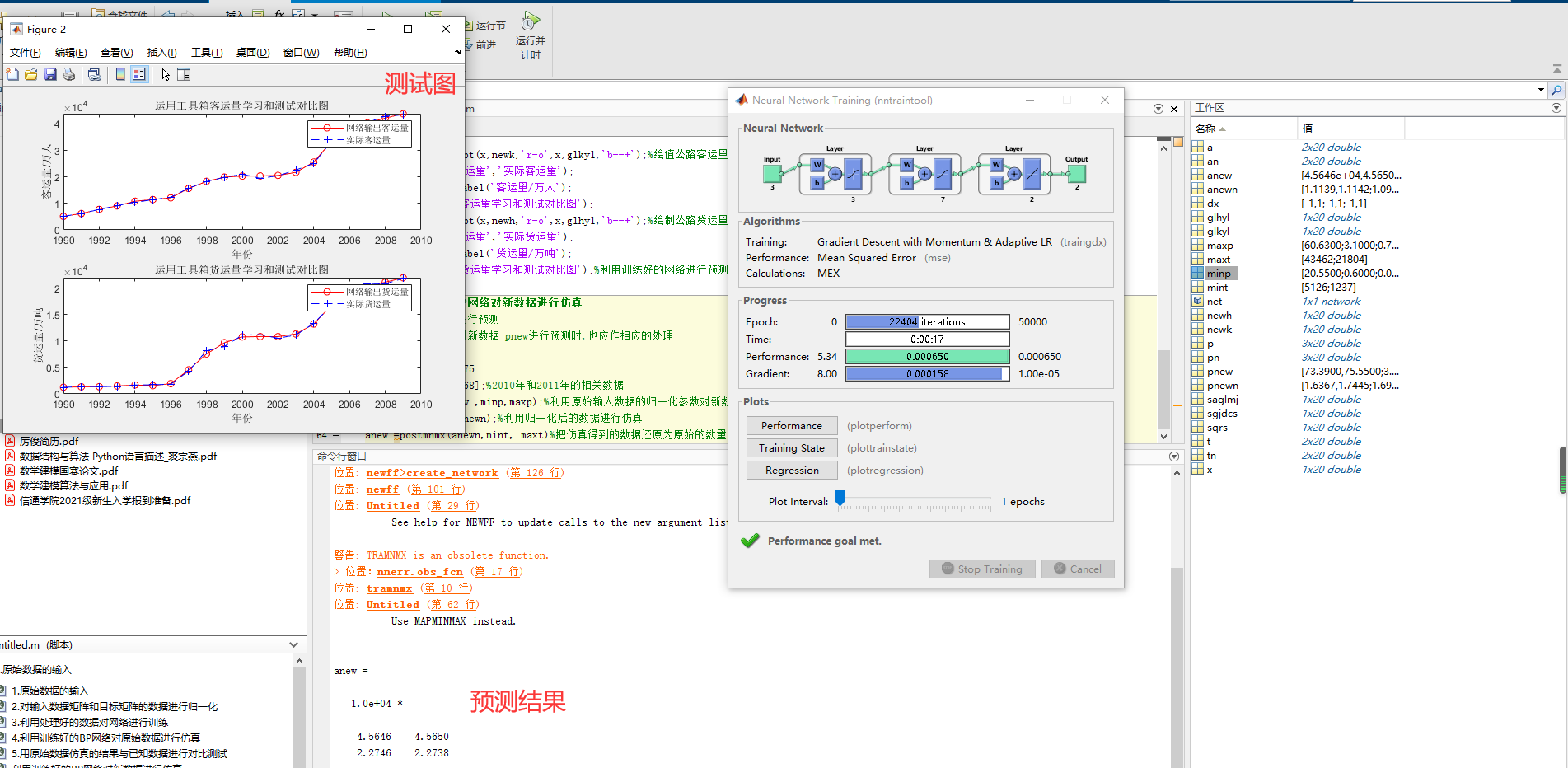
网络的学习曲线
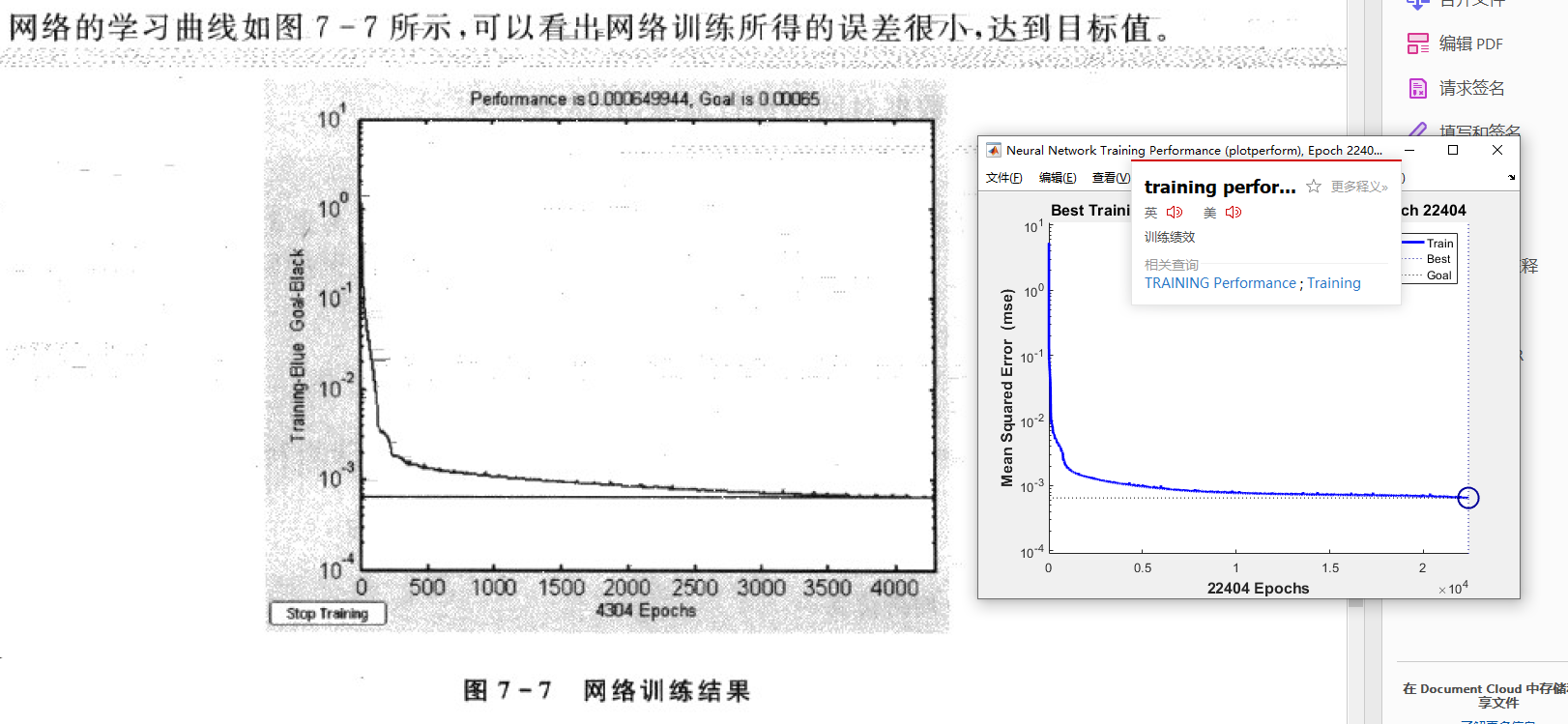

拟合曲线
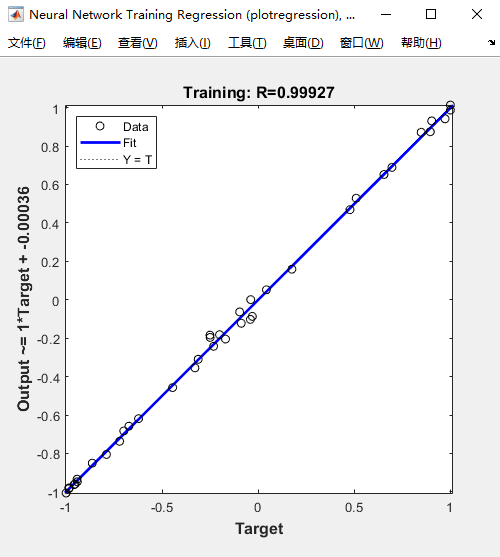
注!!! 上述的原始数据是按行排列的,一行是一个指标,也可以按列排列,但是需要修改格式

神经网络相关函数




激励函数实例
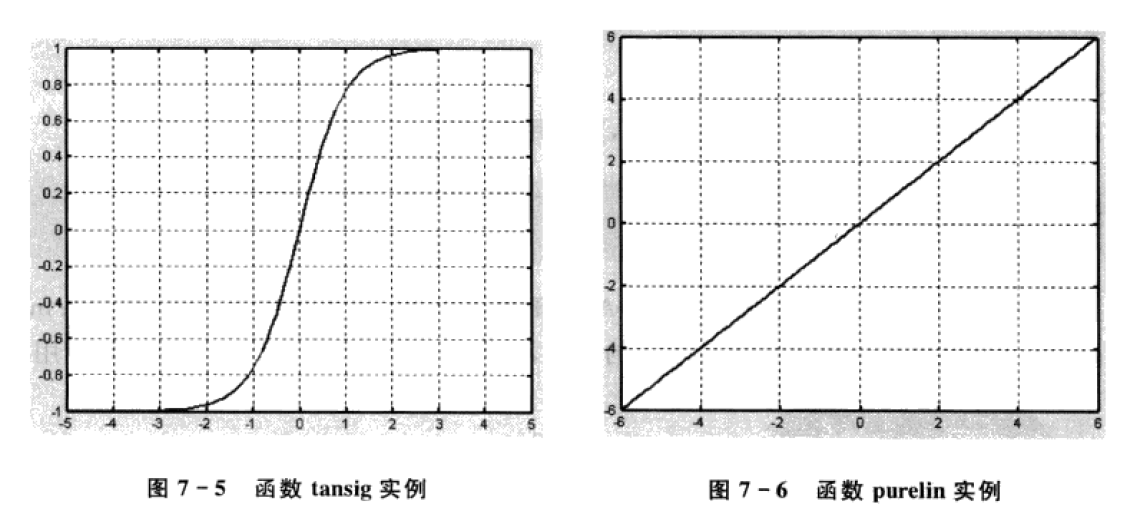
数据预处理和后期处理


基于MATLAB源程序的公路运量预测

代码:
function main()
clc % 清屏
clear all; %清除内存以便加快运算速度
close all; %关闭当前所有figure图像
SamNum=20; %输入样本数量为20
TestSamNum=20; %测试样本数量也是20
ForcastSamNum=2; %预测样本数量为2
HiddenUnitNum=8; %中间层隐节点数量取8,比工具箱程序多了1个
InDim=3; %网络输入维度为3
OutDim=2; %网络输出维度为2
%原始数据
%人数(单位:万人)
sqrs=[20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 ...
41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63];
%机动车数(单位:万辆)
sqjdcs=[0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6...
2.7 2.85 2.95 3.1];
%公路面积(单位:万平方公里)
sqglmj=[0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 ...
0.56 0.59 0.59 0.67 0.69 0.79];
%公路客运量(单位:万人)
glkyl=[5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 ...
22598 25107 33442 36836 40548 42927 43462];
%公路货运量(单位:万吨)
glhyl=[1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 ...
13320 16762 18673 20724 20803 21804];
p=[sqrs;sqjdcs;sqglmj]; %输入数据矩阵
t=[glkyl;glhyl]; %目标数据矩阵
[SamIn,minp,maxp,tn,mint,maxt]=premnmx(p,t); %原始样本对(输入和输出)初始化
rand('state',sum(100*clock)) %依据系统时钟种子产生随机数
NoiseVar=0.01; %噪声强度为0.01(添加噪声的目的是为了防止网络过度拟合)
Noise=NoiseVar*randn(2,SamNum); %生成噪声
SamOut=tn + Noise; %将噪声添加到输出样本上
TestSamIn=SamIn; %这里取输入样本与测试样本相同因为样本容量偏少
TestSamOut=SamOut; %也取输出样本与测试样本相同
MaxEpochs=50000; %最多训练次数为50000
lr=0.035; %学习速率为0.035
E0=0.65*10^(-3); %目标误差为0.65*10^(-3)
W1=0.5*rand(HiddenUnitNum,InDim)-0.1; %初始化输入层与隐含层之间的权值
B1=0.5*rand(HiddenUnitNum,1)-0.1; %初始化输入层与隐含层之间的阈值
W2=0.5*rand(OutDim,HiddenUnitNum)-0.1; %初始化输出层与隐含层之间的权值
B2=0.5*rand(OutDim,1)-0.1; %初始化输出层与隐含层之间的阈值
ErrHistory=[]; %给中间变量预先占据内存
for i=1:MaxEpochs
HiddenOut=logsig(W1*SamIn+repmat(B1,1,SamNum)); % 隐含层网络输出
NetworkOut=W2*HiddenOut+repmat(B2,1,SamNum); % 输出层网络输出
Error=SamOut-NetworkOut; % 实际输出与网络输出之差
SSE=sumsqr(Error) %能量函数(误差平方和)
ErrHistory=[ErrHistory SSE];
if SSE<E0,break, end %如果达到误差要求则跳出学习循环
% 以下六行是BP网络最核心的程序
% 他们是权值(阈值)依据能量函数负梯度下降原理所作的每一步动态调整量
Delta2=Error;
Delta1=W2'*Delta2.*HiddenOut.*(1-HiddenOut);
dW2=Delta2*HiddenOut';
dB2=Delta2*ones(SamNum,1);
dW1=Delta1*SamIn';
dB1=Delta1*ones(SamNum,1);
%对输出层与隐含层之间的权值和阈值进行修正
W2=W2+lr*dW2;
B2=B2+lr*dB2;
%对输入层与隐含层之间的权值和阈值进行修正
W1=W1+lr*dW1;
B1=B1+lr*dB1;
end
HiddenOut=logsig(W1*SamIn+repmat(B1,1,TestSamNum)); % 隐含层输出最终结果
NetworkOut=W2*HiddenOut+repmat(B2,1,TestSamNum); % 输出层输出最终结果
a=postmnmx(NetworkOut,mint,maxt); % 还原网络输出层的结果
x=1990:2009; % 时间轴刻度
newk=a(1,:); % 网络输出客运量
newh=a(2,:); % 网络输出货运量
figure ;
subplot(2,1,1);plot(x,newk,'r-o',x,glkyl,'b--+') %绘值公路客运量对比图;
legend('网络输出客运量','实际客运量');
xlabel('年份');ylabel('客运量/万人');
subplot(2,1,2);plot(x,newh,'r-o',x,glhyl,'b--+') %绘制公路货运量对比图;
legend('网络输出货运量','实际货运量');
xlabel('年份');ylabel('货运量/万吨');
% 利用训练好的网络进行预测
% 当用训练好的网络对新数据pnew进行预测时,也应作相应的处理
pnew=[73.39 75.55
3.9635 4.0975
0.9880 1.0268]; %2010年和2011年的相关数据;
pnewn=tramnmx(pnew,minp,maxp); %利用原始输入数据的归一化参数对新数据进行归一化;
HiddenOut=logsig(W1*pnewn+repmat(B1,1,ForcastSamNum)); % 隐含层输出预测结果
anewn=W2*HiddenOut+repmat(B2,1,ForcastSamNum); % 输出层输出预测结果
%把网络预测得到的数据还原为原始的数量级;
anew=postmnmx(anewn,mint,maxt)
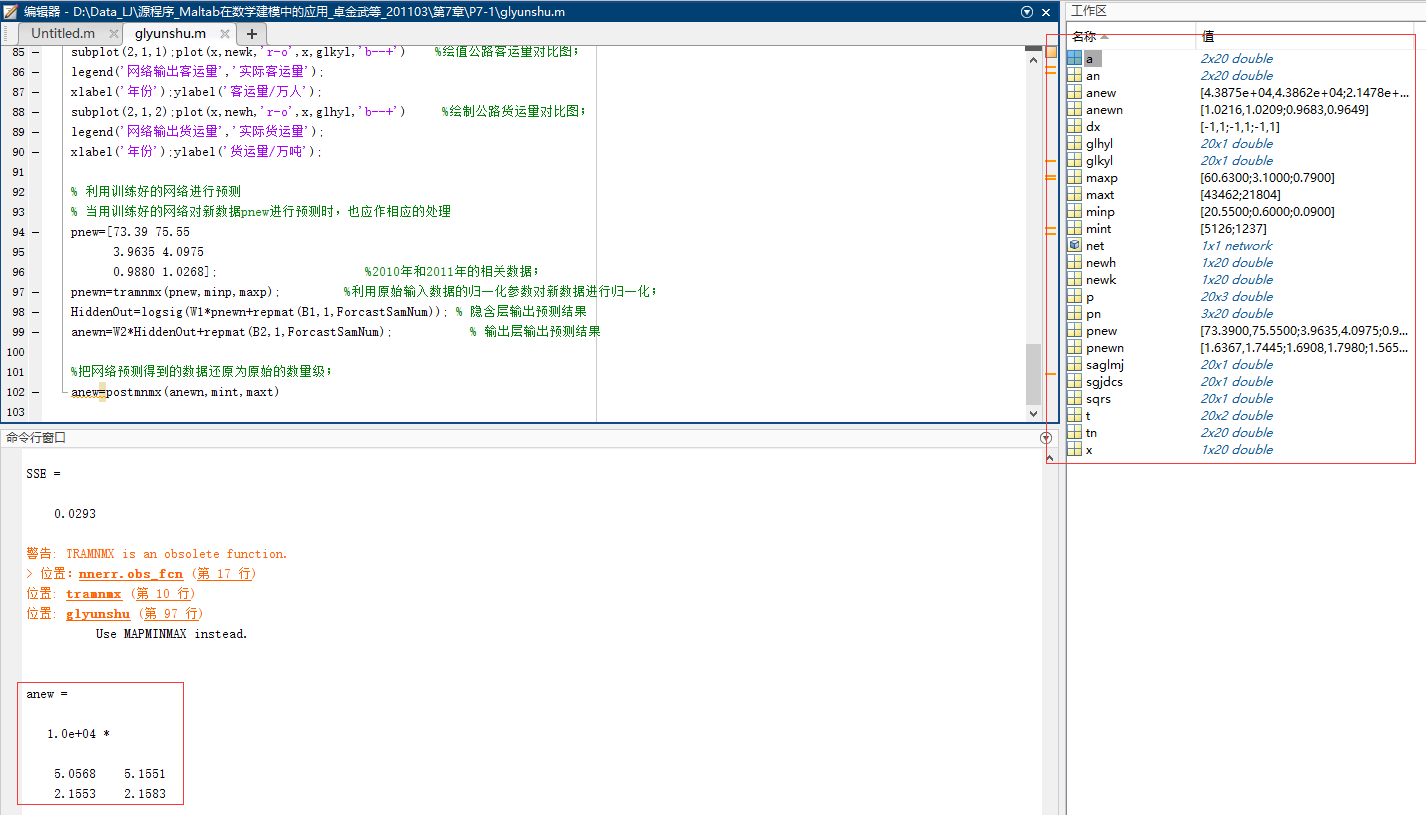
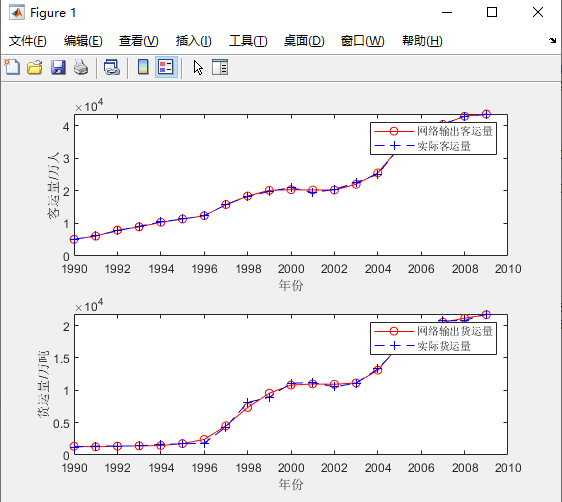
转载请注明出处,欢迎讨论和交流!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号