数模-元胞自动机
简介

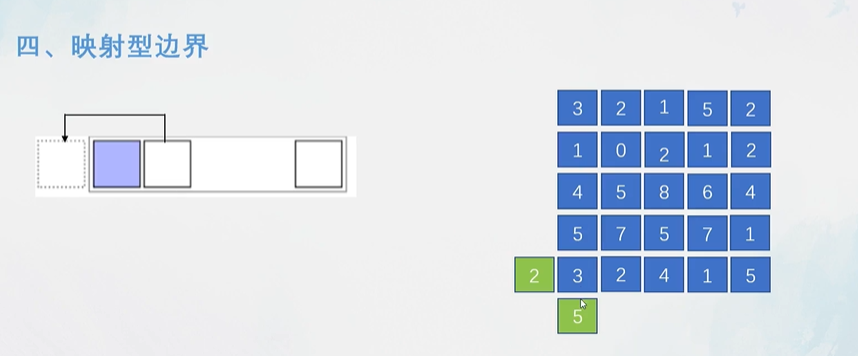
构成
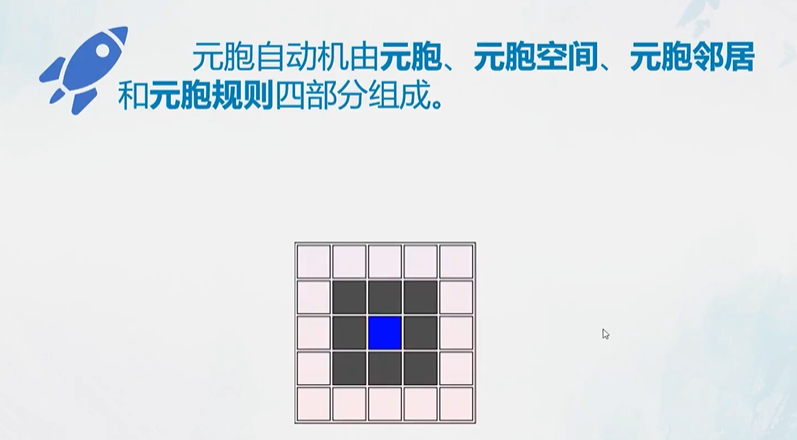
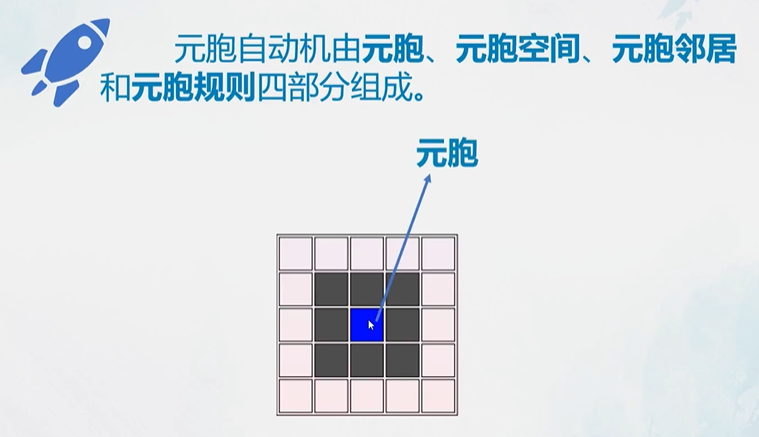
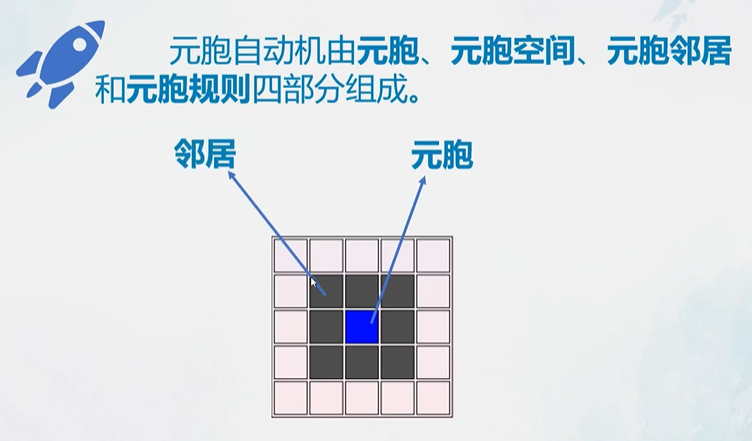
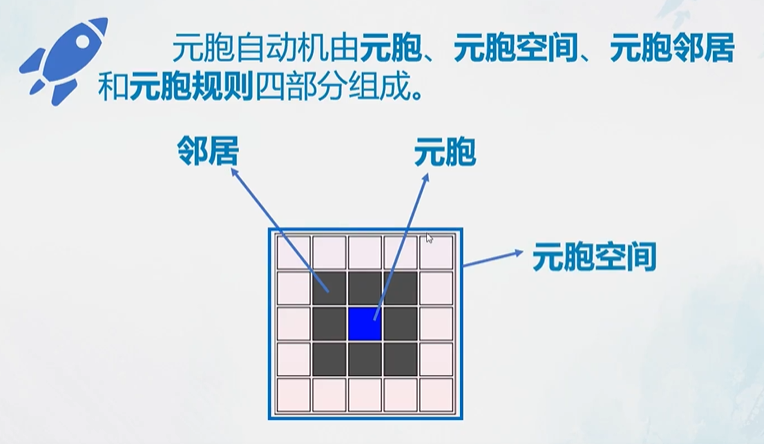
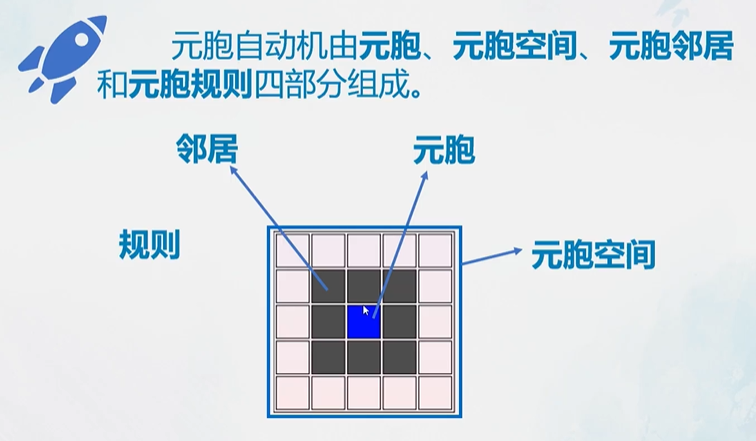
元胞


元胞空间
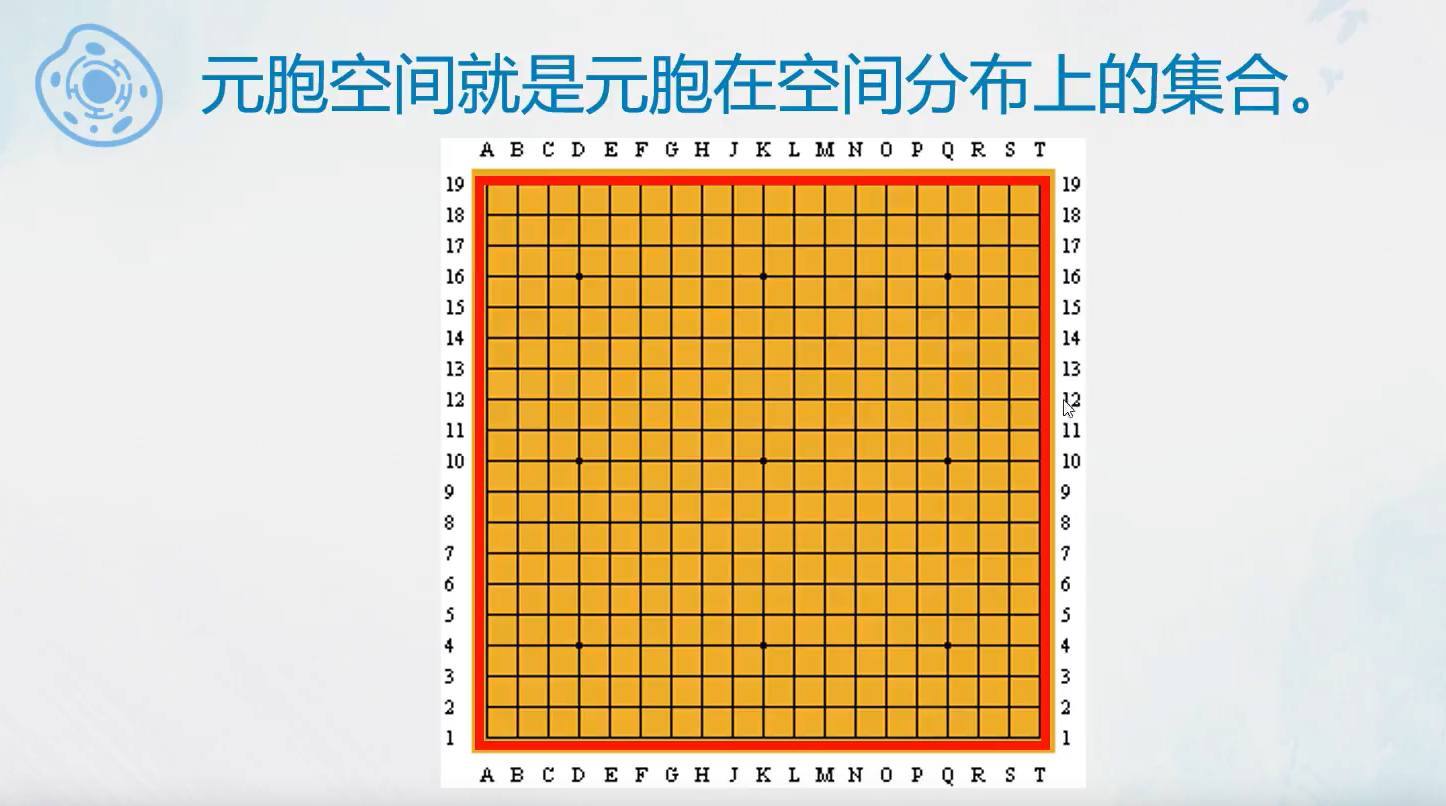

用的最多的是正方形空间
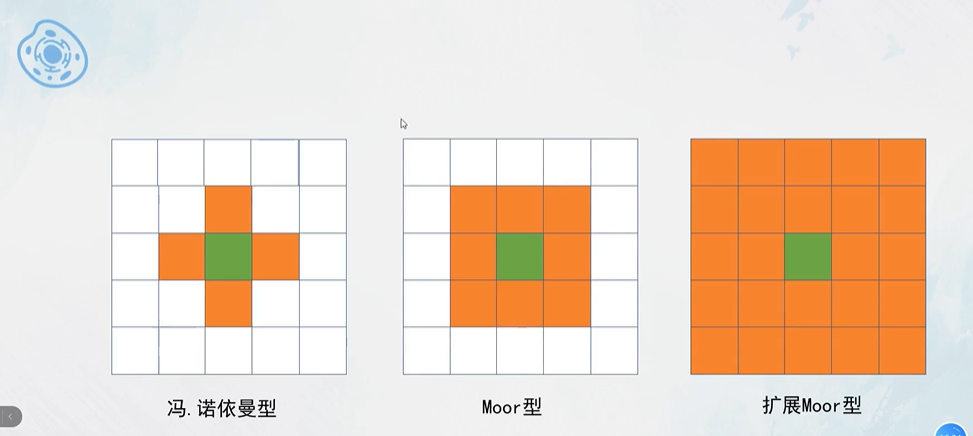
邻居

常见的邻居状态


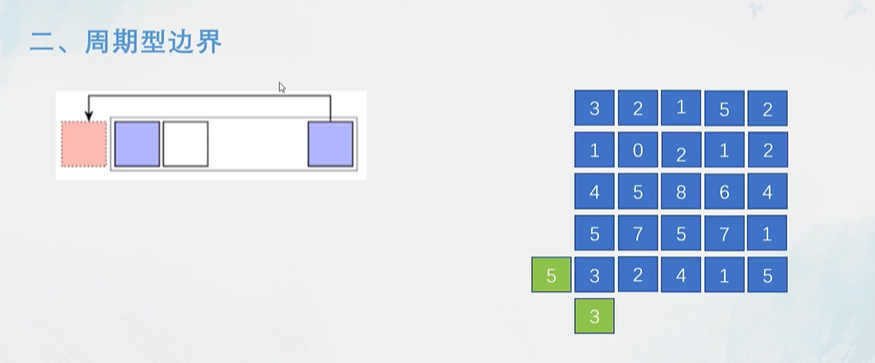


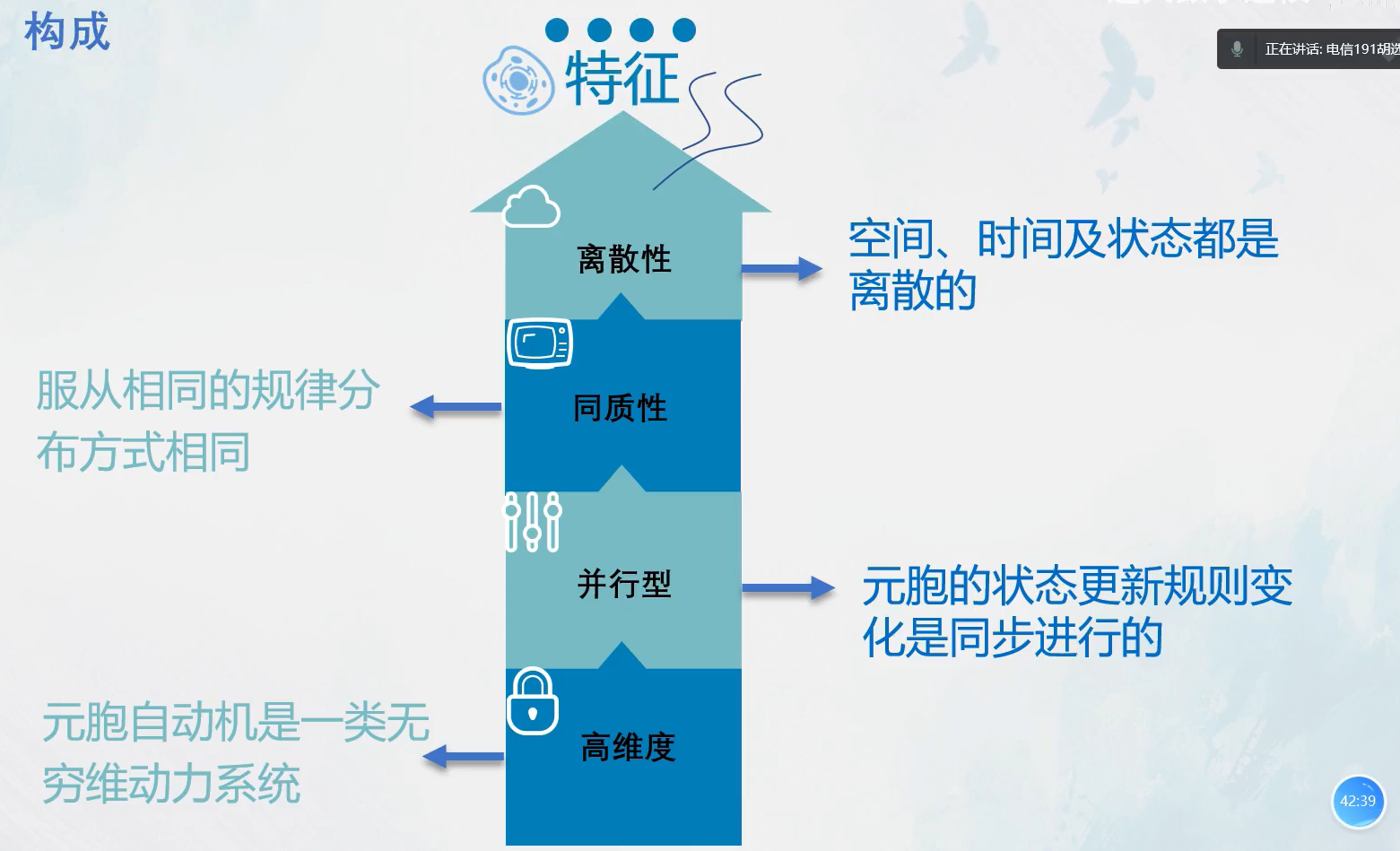
特征
初等元胞自动机

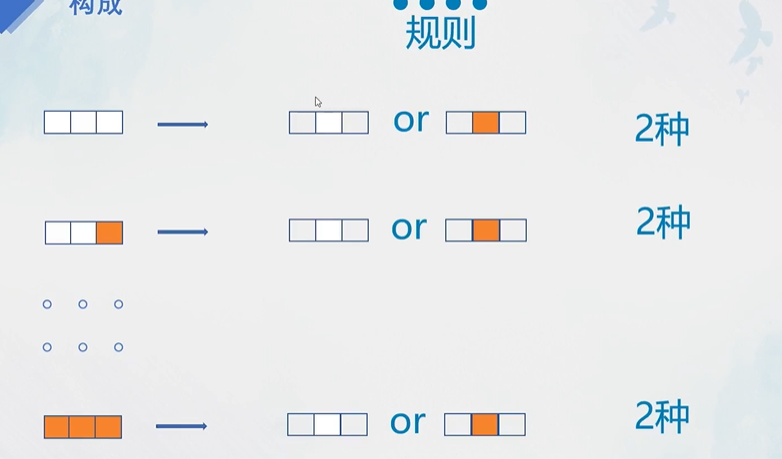
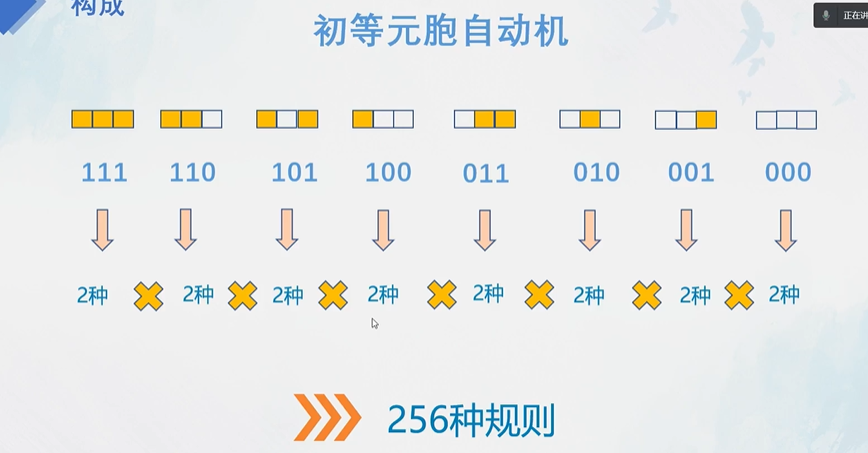
所以一共有256种规则
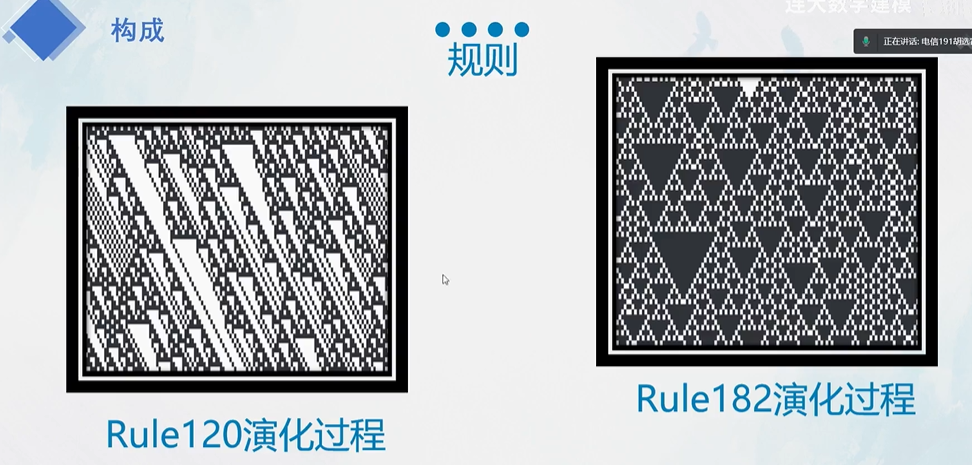
实例
奇偶规则

参考博文
MATLAB中的imagesc函数
代码实现:
clc
clear
n=200;
Se=zeros(n);
z=zeros(n);
Se(n/2-2:n/2+2,n/2-2:n/2+2)=1;
Ch=imagesc(cat(3,Se,z,z));%把这个矩阵图画出来
axis square;
Sd=zeros(n+2);%固定型边界条件
while(1)
Sd(2:n+1,2:n+1)=Se;%中间是Se,边缘是我们的边界条件
sum=Sd(1:n,2:n+1)+Sd(3:n+2,2:n+1)+Sd(2:n+1,1:n)+Sd(2:n+1,3:n+2);
%这个就是直接对每个元素进行上下左右的值的相加,不需要遍历
Se=mod(sum,2);
set(Ch,'cdata',cat(3,Se,z,z))
pause(0.03)
end
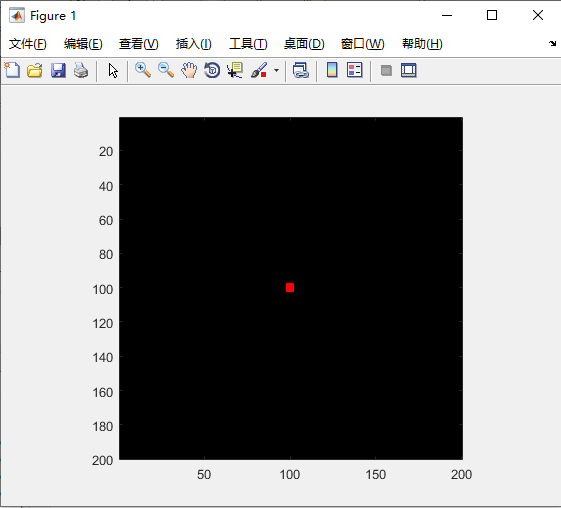
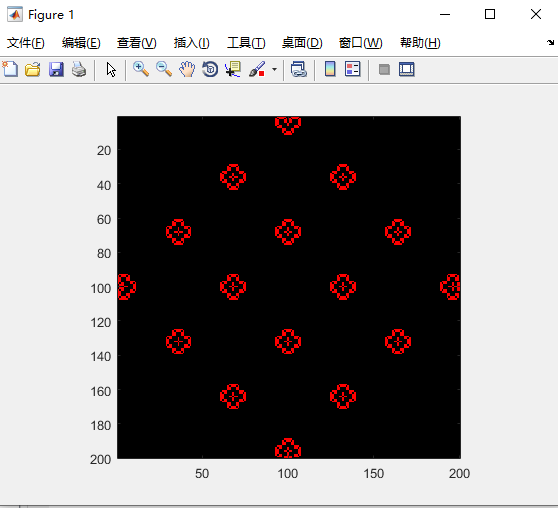
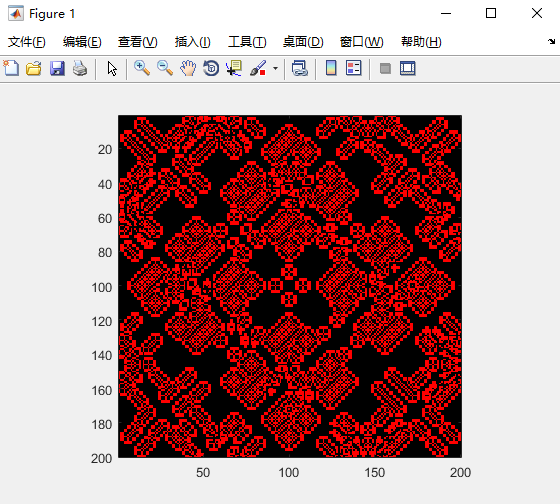
生命游戏

原始时刻:
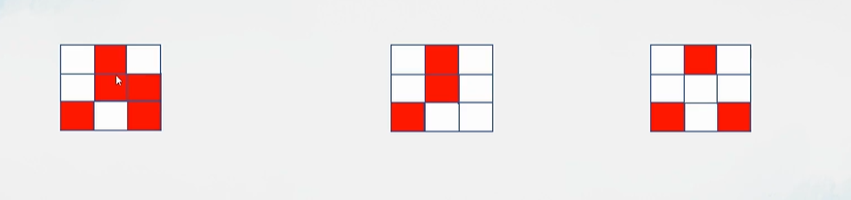
下一时刻:
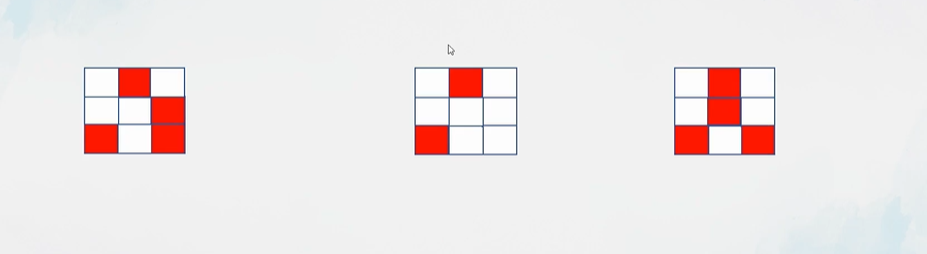
代码
clc
clear
n=200;
p=0.4;
z=zeros(n);
Se=rand(n)<p;%若小于p则为1,若大于p则为0
Sd=zeros(n+2);%矩阵初始化
Ph=image(cat(3,Se,z,z));%把这个矩阵图画出来
axis square;
while(1)
Sd(2:n+1,2:n+1)=Se;%中间是Se,边缘是我们的边界条件
sum=Sd(1:n,2:n+1)+Sd(3:n+2,2:n+1)+Sd(2:n+1,1:n)+Sd(2:n+1,3:n+2)+...
Sd(1:n,1:n)+Sd(3:n+2,1:n)+Sd(1:n,3:n+2)+Sd(3:n+2,3:n+2);
%这个就是直接对每个元素进行8个邻居的值的相加,不需要遍历
for i=1:n
for j=1:n
if sum(i,j)==3 ||(sum(i,j)==2 && Se(i,j)==1) %生的条件
Se(i,j)=1;
else
Se(i,j)=0;
end
end
end
set(Ph,'cdata',cat(3,Se,z,z))%更新可视化
drawnow
end
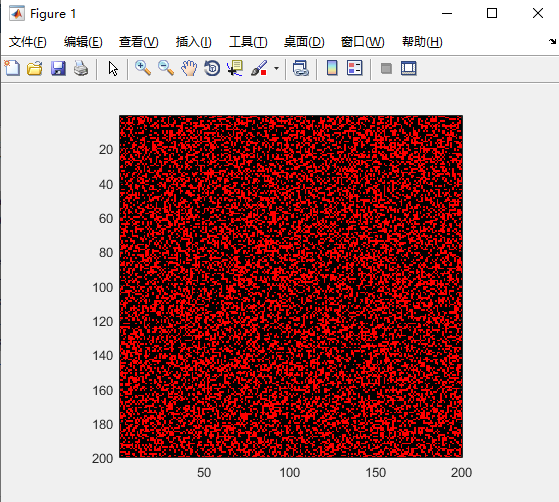
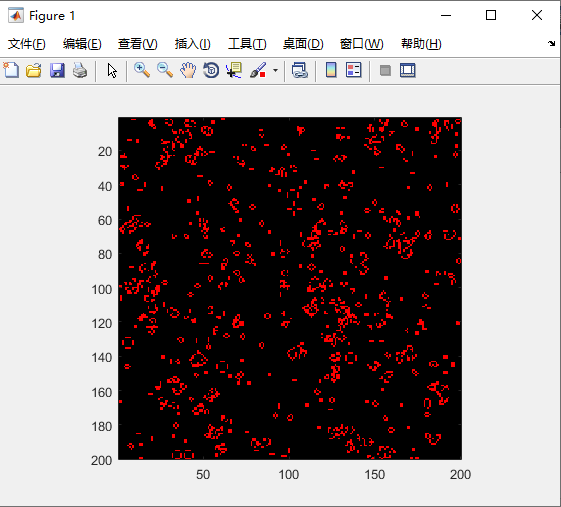
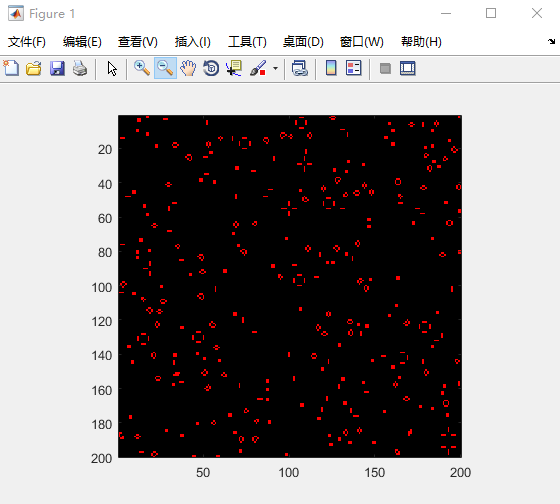
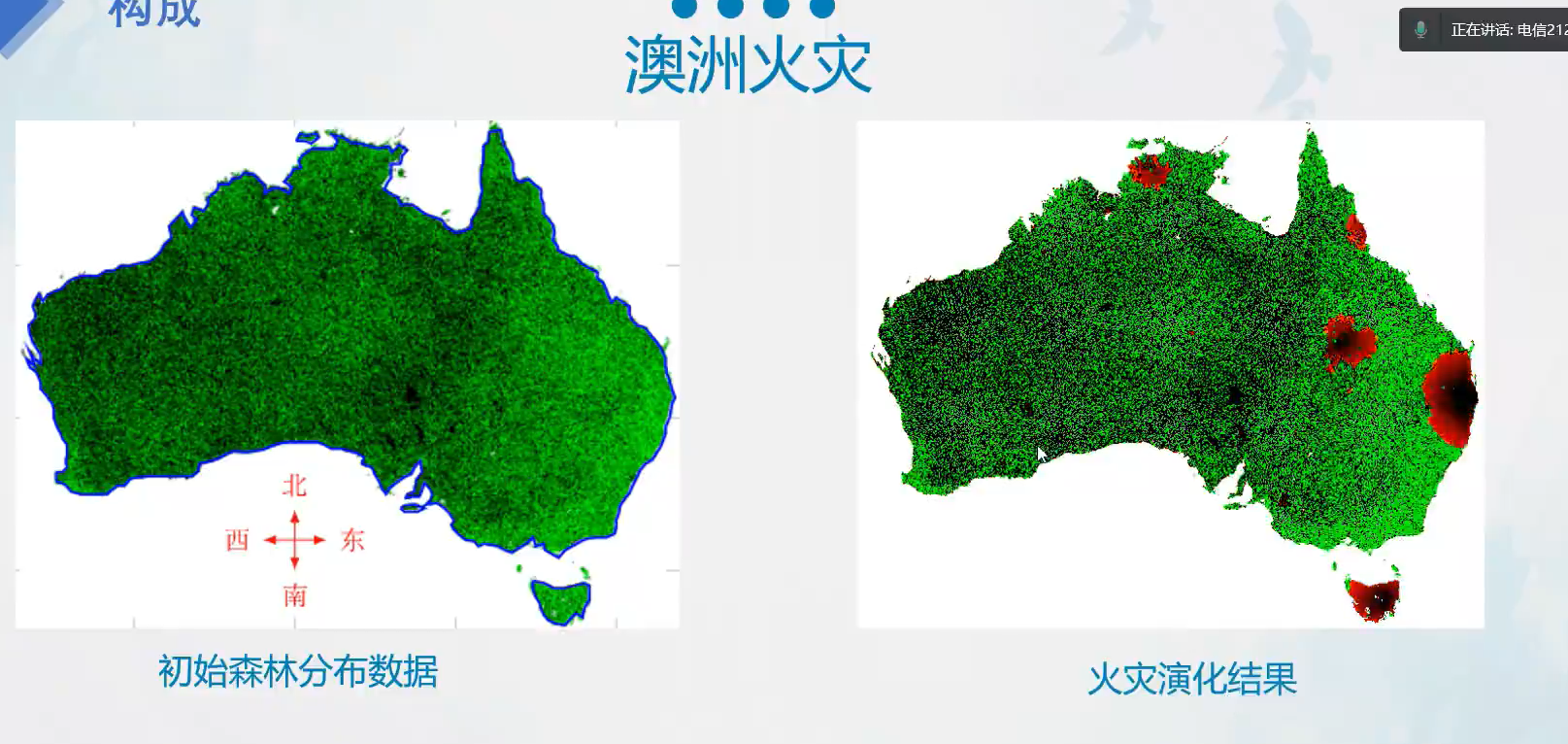
澳洲火灾


代码:
clc
clear
n=300; % 定义表示森林的矩阵大小
Plight=5e-6;Pgrowth=1e-2; % 定义闪电和生长的概率
UL=[n,1:n-1];DR=[2:n,1]; % 定义上左,下右邻居
%UL=[300,1,2,3,...,299]
%DR=[2,3,...300,1]
veg=zeros(n,n); % 初始化表示森林的矩阵
imh=image(cat(3,veg,veg,veg)); % 可视化表示森林的矩阵
% veg = 空地为0 着火为1 树为2
for i=1:3000
sum=(veg(UL,:)==1)+(veg(:,UL)==1)+(veg(:,DR)==1)+(veg(DR,:)==1);
%计算所有邻居的着火点
%根据规则更新森林矩阵,是否树=是否树-是否着火的树+是否新生的树(0-1运算)
veg=2*(veg==2)-((veg==2)&(sum>0 | (rand(n,n)<Plight)))+2*((veg==0)&rand(n,n)<Pgrowth);
% (veg==2)判断为树
% ((veg==2)&(sum>0 | (rand(n,n)<Plight)))着火点
% ((veg==0)&rand(n,n)<Pgrowth) 新生的树
% 当是树的时候为1,然后着火点也为1,这时候树前面×2,则相减为1,刚好对应着着火的状态
set(imh,'cdata',cat(3,(veg==1),(veg==2),zeros(n)))
drawnow %可视化表示森林的矩阵
end
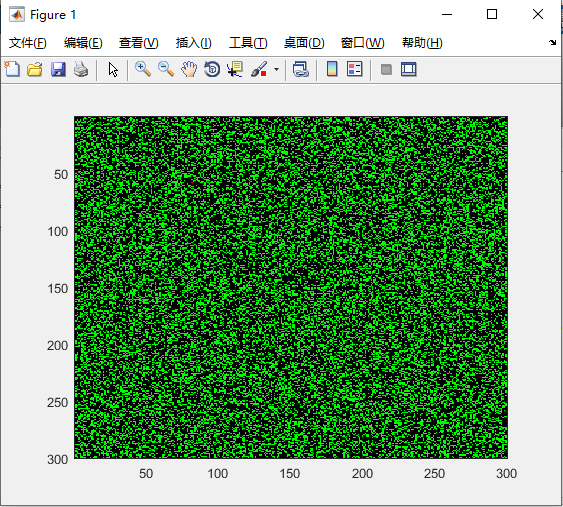
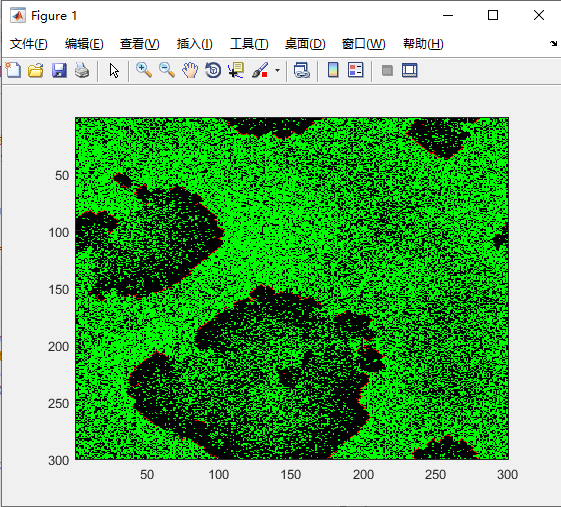
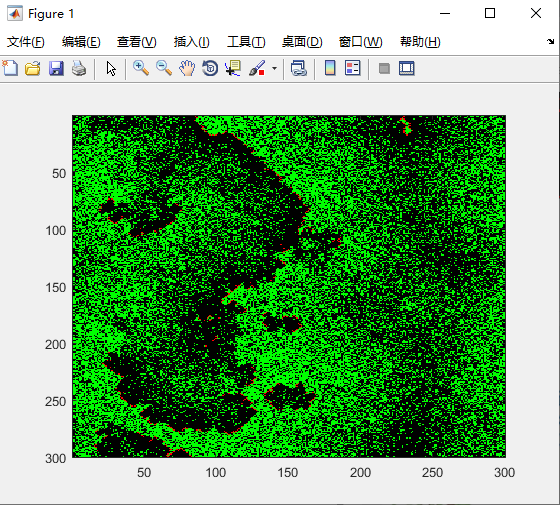
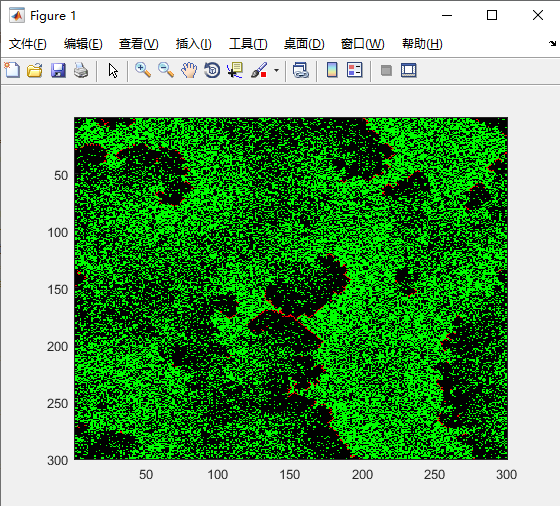
逐渐长出树,然后燃烧,然后再长出新的树
实际应用中,只需要把森林的初始数据代入即可
转载请注明出处,欢迎讨论和交流!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号