数模-主成分分析

主成分分析(Principal Component Analysis,PCA)

主成分分析是一种降维算法，它能将多个指标转换为少数几个主成分，这些主成分是原始变量的线性组合，且彼此之间互不相关，其能反映出原始数据的大部分信息。一般来说，当研究的问题涉及到多变量且变量之间存在很强的相关性时，我们可考虑使用主成分分析的方法来对数据进行简化。

问题的提出

在实际问题研究中，多变量问题是经常会遇到的。变量太多，无疑会增加分析问题的难度与复杂性，而且在许多实际问题中，多个变量之间是具有一定的相关关系的。

因此，人们会很自然地想到，能否在相关分析的基础上，用较少的新变量代替原来较多的旧变量，而且使这些较少的新变量尽可能多地保留原来变量所反映的信息？

主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析方法。

从数学角度来看，这是一种降维处理技术

数据降维的作用

降维是将高维度的数据（指标太多）保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。

在实际的生产和应用中，降维在一定的信息损失范围内，可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。

降维具有如下一些优点：

• 使得数据集更易使用
• 降低算法的计算开销
• 去除噪声
• 使得结果容易理解

一个简单的例子

主成分分析的思想

严谨的数学符号

PCA的计算步骤

例题讲解1

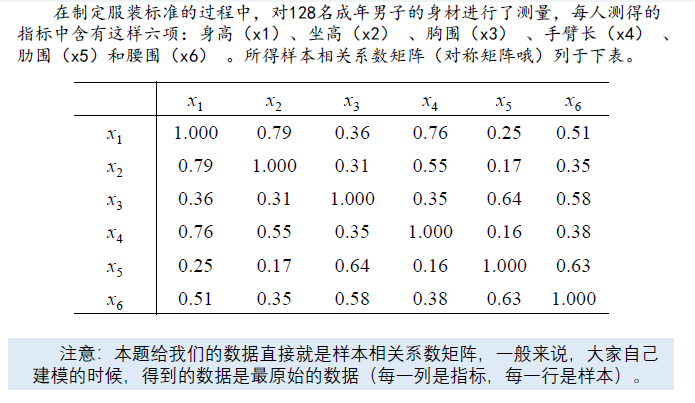
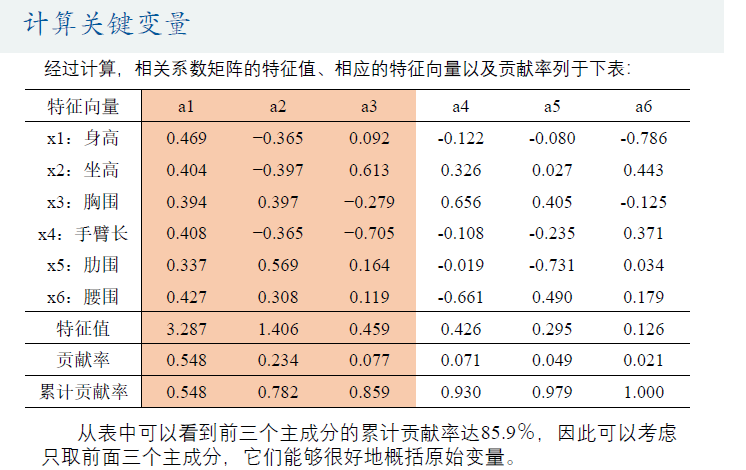
例题讲解2

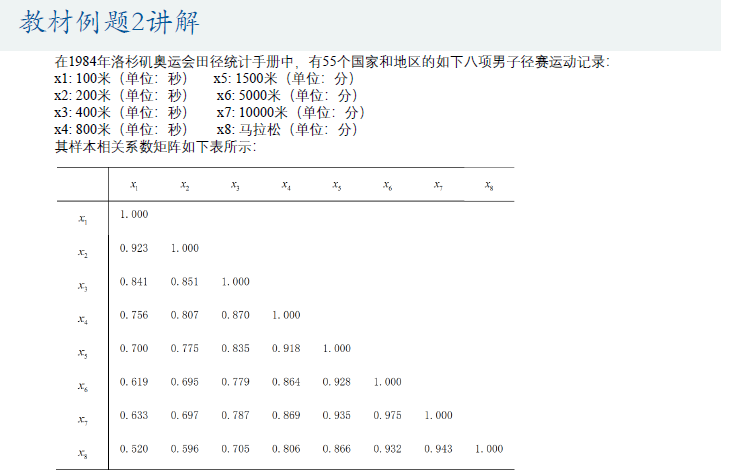
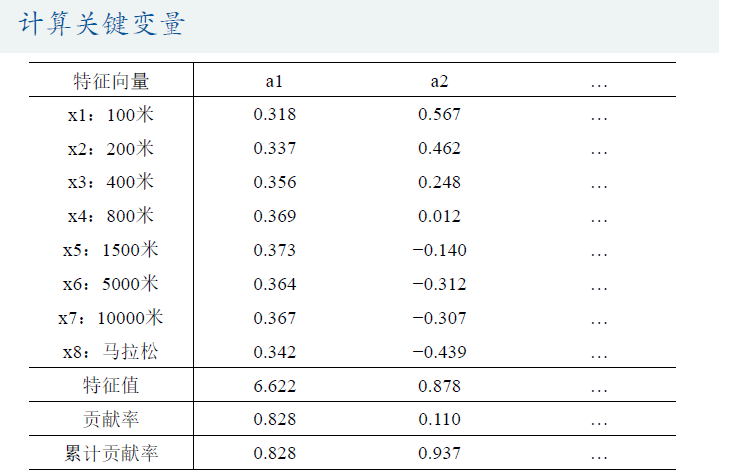
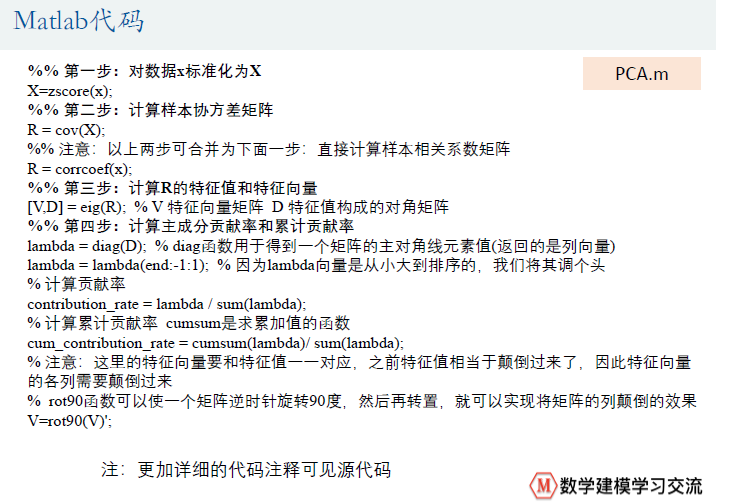
代码：

clear;clc
 load data1.mat   % 主成分聚类
%  load data2.mat   % 主成分回归

% 注意，这里可以对数据先进行描述性统计
% 描述性统计的内容见第5讲.相关系数
[n,p] = size(x);  % n是样本个数，p是指标个数

%% 第一步：对数据x标准化为X
X=zscore(x);   % matlab内置的标准化函数（x-mean(x)）/std(x)

%% 第二步：计算样本协方差矩阵
R = cov(X);

%% 注意：以上两步可合并为下面一步：直接计算样本相关系数矩阵
R = corrcoef(x);
disp('样本相关系数矩阵为：')
disp(R)

%% 第三步：计算R的特征值和特征向量
% 注意：R是半正定矩阵，所以其特征值不为负数
% R同时是对称矩阵，Matlab计算对称矩阵时，会将特征值按照从小到大排列哦
% eig函数的详解见第一讲层次分析法的视频
[V,D] = eig(R);  % V 特征向量矩阵  D 特征值构成的对角矩阵


%% 第四步：计算主成分贡献率和累计贡献率
lambda = diag(D);  % diag函数用于得到一个矩阵的主对角线元素值(返回的是列向量)
lambda = lambda(end:-1:1);  % 因为lambda向量是从小大到排序的，我们将其调个头
contribution_rate = lambda / sum(lambda);  % 计算贡献率
cum_contribution_rate = cumsum(lambda)/ sum(lambda);   % 计算累计贡献率  cumsum是求累加值的函数
disp('特征值为：')
disp(lambda')  % 转置为行向量，方便展示
disp('贡献率为：')
disp(contribution_rate')
disp('累计贡献率为：')
disp(cum_contribution_rate')
disp('与特征值对应的特征向量矩阵为：')
% 注意：这里的特征向量要和特征值一一对应，之前特征值相当于颠倒过来了，因此特征向量的各列需要颠倒过来
%  rot90函数可以使一个矩阵逆时针旋转90度，然后再转置，就可以实现将矩阵的列颠倒的效果
V=rot90(V)';
disp(V)


%% 计算我们所需要的主成分的值
m =input('请输入需要保存的主成分的个数:  ');
F = zeros(n,m);  %初始化保存主成分的矩阵（每一列是一个主成分）
for i = 1:m
    ai = V(:,i)';   % 将第i个特征向量取出，并转置为行向量
    Ai = repmat(ai,n,1);   % 将这个行向量重复n次，构成一个n*p的矩阵
    F(:, i) = sum(Ai .* X, 2);  % 注意，对标准化的数据求了权重后要计算每一行的和
end

%% (1)主成分聚类 ： 将主成分指标所在的F矩阵复制到Excel表格，然后再用Spss进行聚类
% 在Excel第一行输入指标名称（F1,F2, ..., Fm）
% 双击Matlab工作区的F,进入变量编辑中，然后复制里面的数据到Excel表格
% 导出数据之后，我们后续的分析就可以在Spss中进行。

%%（2）主成分回归：将x使用主成分得到主成分指标，并将y标准化，接着导出到Excel，然后再使用Stata回归
% Y = zscore(y);  % 一定要将y进行标准化哦~
% 在Excel第一行输入指标名称（Y,F1, F2, ..., Fm）
% 分别双击Matlab工作区的Y和F,进入变量编辑中，然后复制里面的数据到Excel表格
% 导出数据之后，我们后续的分析就可以在Stata中进行。





% % 注意：代码文件仅供参考，一定不要直接用于自己的数模论文中
% % 国赛对于论文的查重要求非常严格，代码雷同也算作抄袭
% % 视频中提到的附件可在售后群（购买后收到的那个无忧自动发货的短信中有加入方式）的群文件中下载。包括讲义、代码、我视频中推荐的资料等。
% % 关注我的微信公众号《数学建模学习交流》，后台发送“软件”两个字，可获得常见的建模软件下载方法；发送“数据”两个字，可获得建模数据的获取方法；发送“画图”两个字，可获得数学建模中常见的画图方法。另外，也可以看看公众号的历史文章，里面发布的都是对大家有帮助的技巧。
% % 购买更多优质精选的数学建模资料，可关注我的微信公众号《数学建模学习交流》，在后台发送“买”这个字即可进入店铺(我的微店地址：https://weidian.com/?userid=1372657210)进行购买。
% % 视频价格不贵，但价值很高。单人购买观看只需要58元，三人购买人均仅需46元，视频本身也是下载到本地观看的，所以请大家不要侵犯知识产权，对视频或者资料进行二次销售。
% % 如何修改代码避免查重的方法：https://www.bilibili.com/video/av59423231（必看）

其中导入的数据，多少行就代表了多少个样本，多少列就代表多少个指标

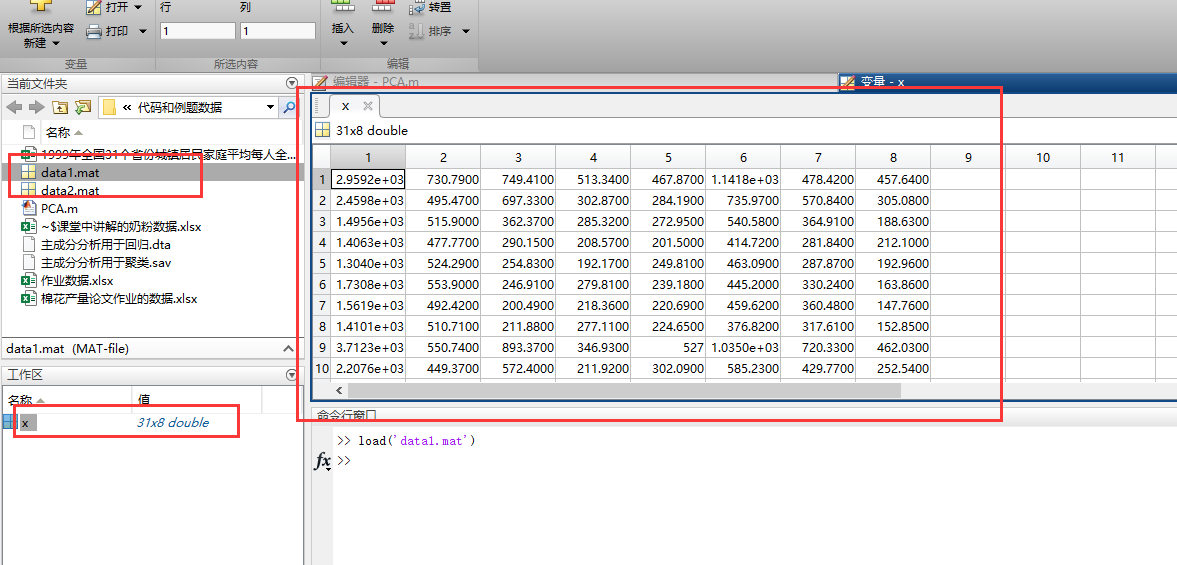
运行

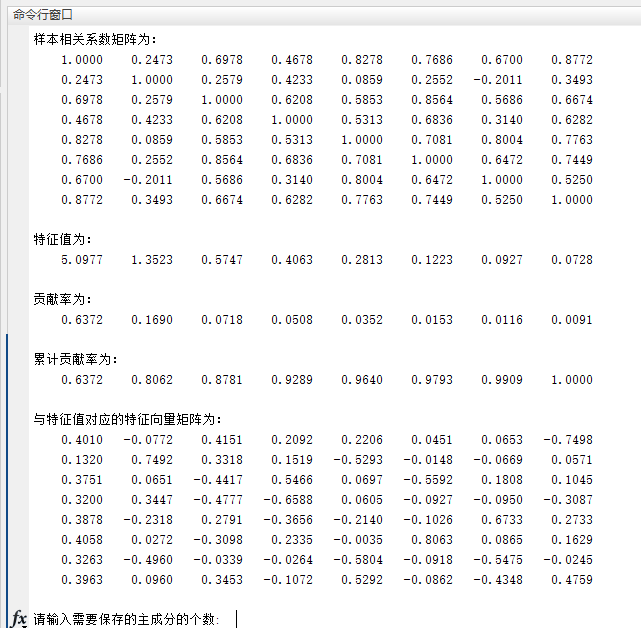
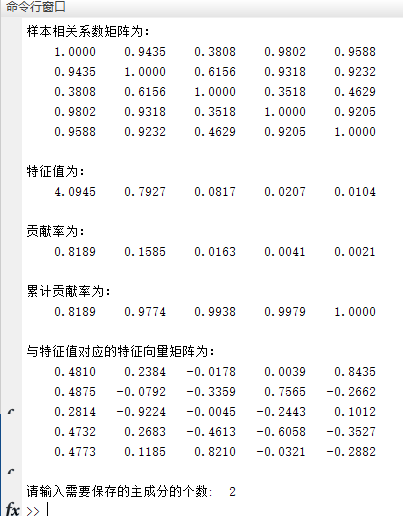
运行完之后输入要保存的主成分的个数

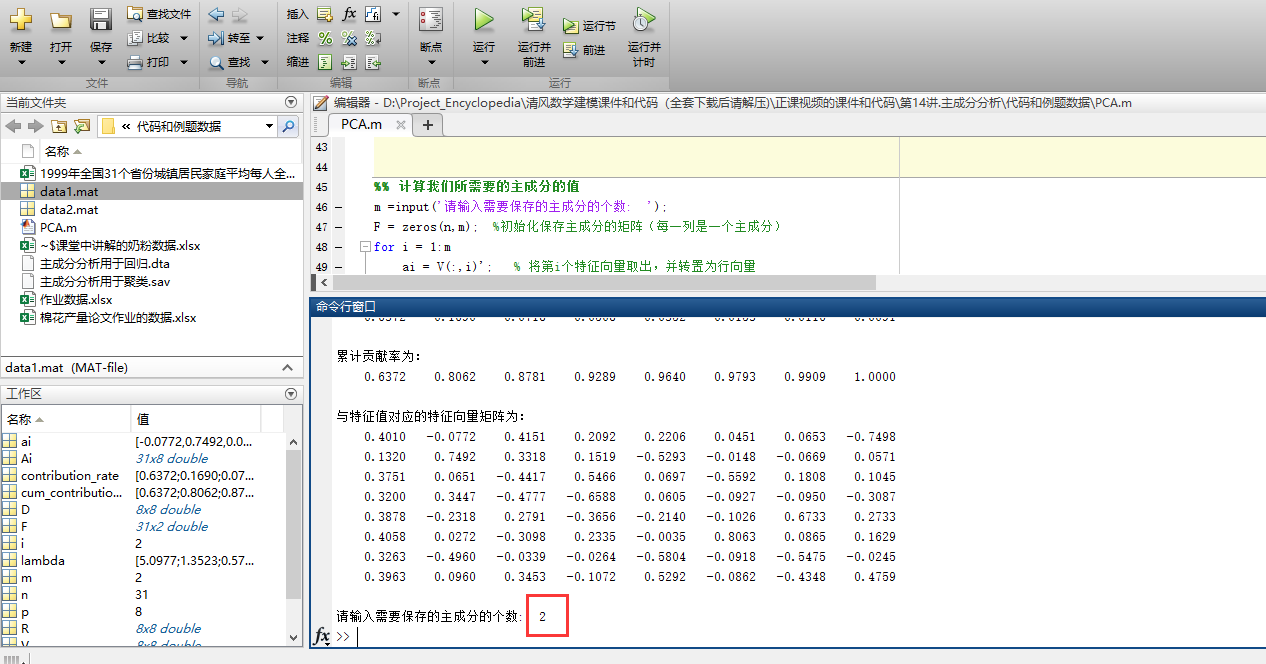
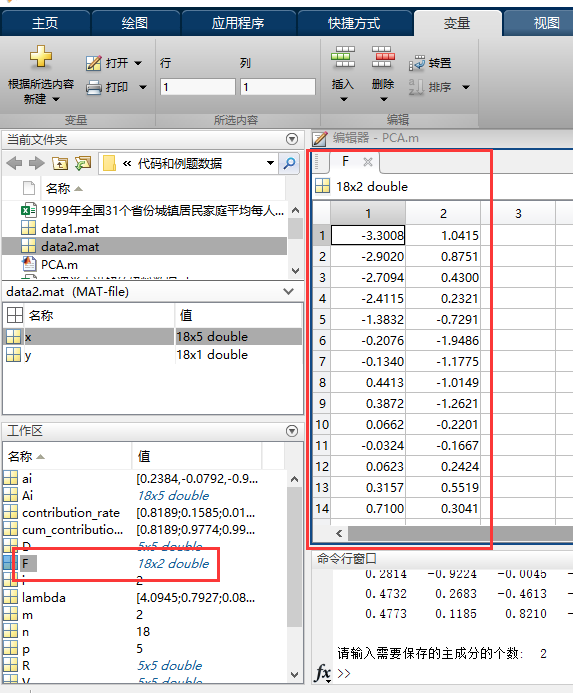
F就是我们最后要保存的主成分数目和系数

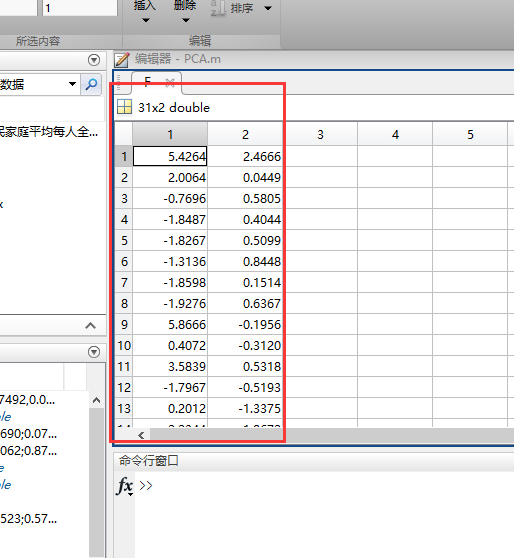
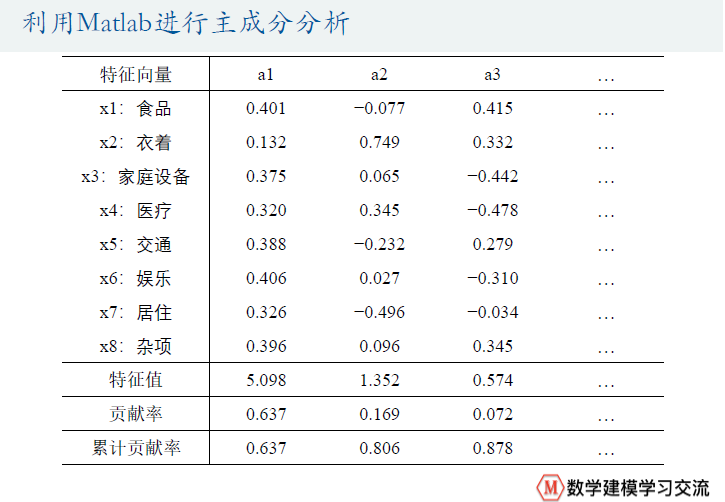
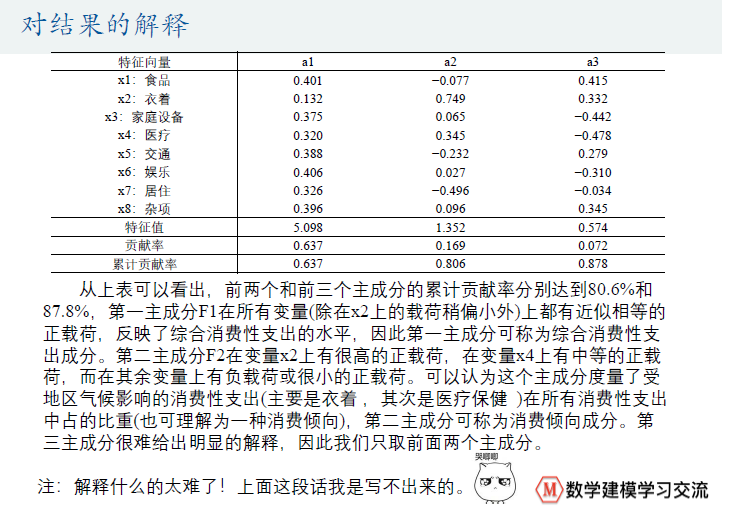
然后就用SPSS软件进行聚类分析☆

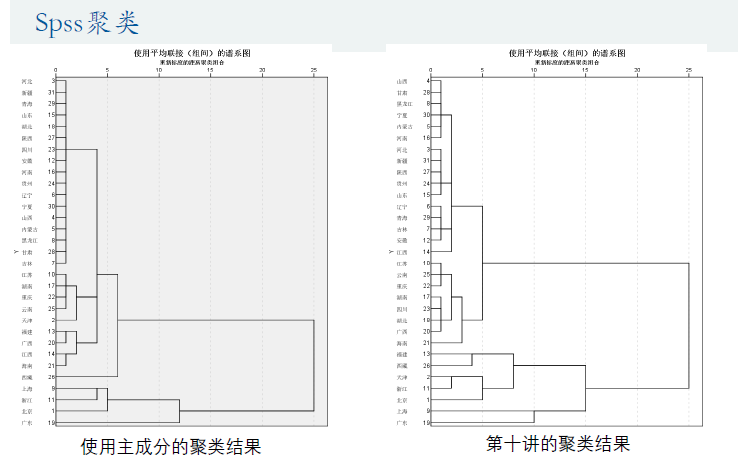
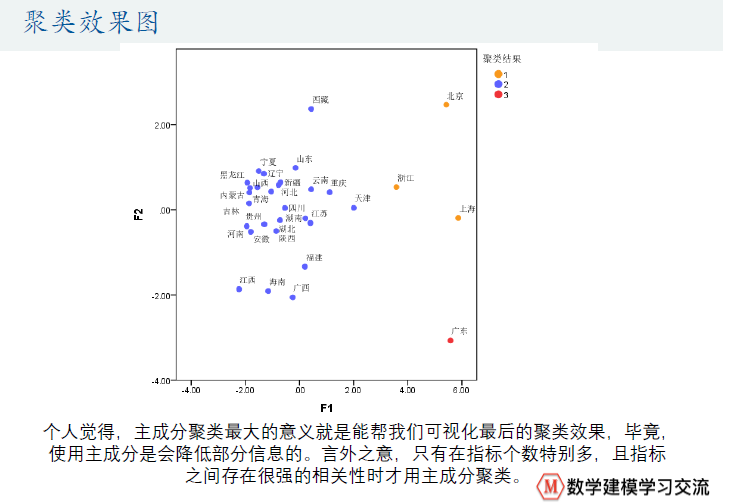
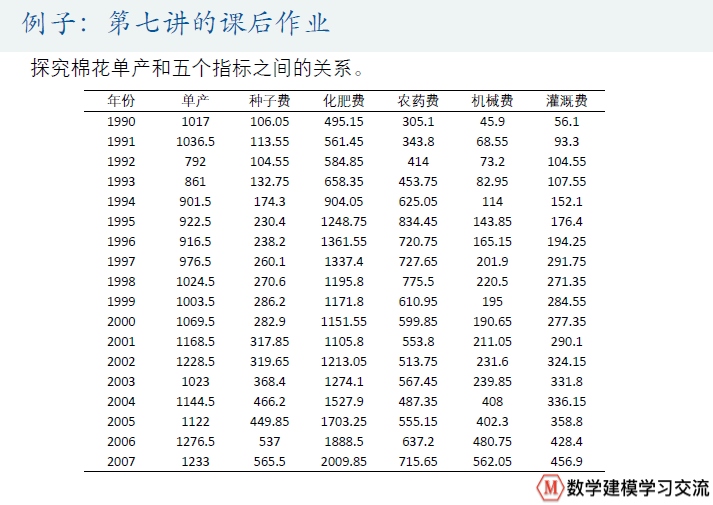
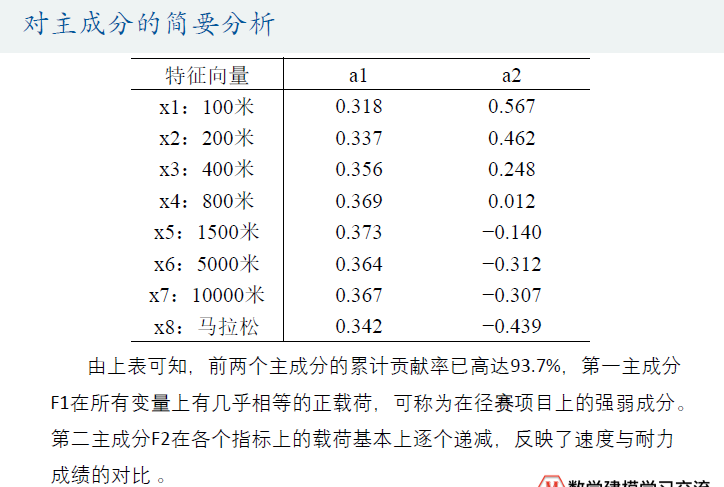
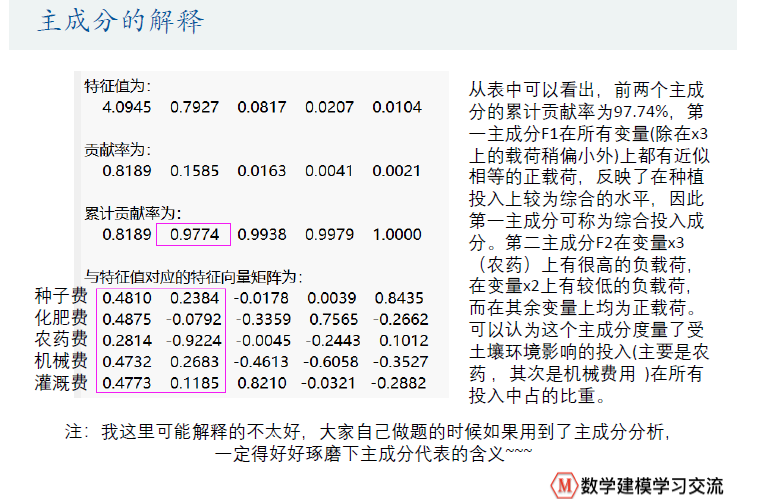
对这道例题进行主成分分析

数据集导入

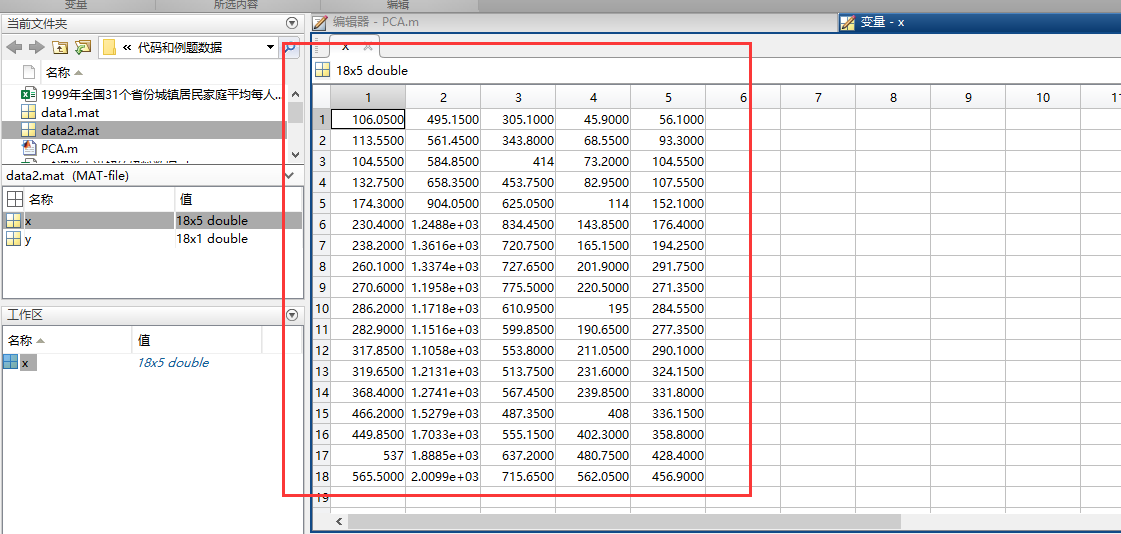
代码（跟上一个例题一样的，就是数据集变了一下）：

clear;clc
% load data1.mat   % 主成分聚类
  load data2.mat   % 主成分回归

% 注意，这里可以对数据先进行描述性统计
% 描述性统计的内容见第5讲.相关系数
[n,p] = size(x);  % n是样本个数，p是指标个数

%% 第一步：对数据x标准化为X
X=zscore(x);   % matlab内置的标准化函数（x-mean(x)）/std(x)

%% 第二步：计算样本协方差矩阵
R = cov(X);

%% 注意：以上两步可合并为下面一步：直接计算样本相关系数矩阵
R = corrcoef(x);
disp('样本相关系数矩阵为：')
disp(R)

%% 第三步：计算R的特征值和特征向量
% 注意：R是半正定矩阵，所以其特征值不为负数
% R同时是对称矩阵，Matlab计算对称矩阵时，会将特征值按照从小到大排列哦
% eig函数的详解见第一讲层次分析法的视频
[V,D] = eig(R);  % V 特征向量矩阵  D 特征值构成的对角矩阵


%% 第四步：计算主成分贡献率和累计贡献率
lambda = diag(D);  % diag函数用于得到一个矩阵的主对角线元素值(返回的是列向量)
lambda = lambda(end:-1:1);  % 因为lambda向量是从小大到排序的，我们将其调个头
contribution_rate = lambda / sum(lambda);  % 计算贡献率
cum_contribution_rate = cumsum(lambda)/ sum(lambda);   % 计算累计贡献率  cumsum是求累加值的函数
disp('特征值为：')
disp(lambda')  % 转置为行向量，方便展示
disp('贡献率为：')
disp(contribution_rate')
disp('累计贡献率为：')
disp(cum_contribution_rate')
disp('与特征值对应的特征向量矩阵为：')
% 注意：这里的特征向量要和特征值一一对应，之前特征值相当于颠倒过来了，因此特征向量的各列需要颠倒过来
%  rot90函数可以使一个矩阵逆时针旋转90度，然后再转置，就可以实现将矩阵的列颠倒的效果
V=rot90(V)';
disp(V)


%% 计算我们所需要的主成分的值
m =input('请输入需要保存的主成分的个数:  ');
F = zeros(n,m);  %初始化保存主成分的矩阵（每一列是一个主成分）
for i = 1:m
    ai = V(:,i)';   % 将第i个特征向量取出，并转置为行向量
    Ai = repmat(ai,n,1);   % 将这个行向量重复n次，构成一个n*p的矩阵
    F(:, i) = sum(Ai .* X, 2);  % 注意，对标准化的数据求了权重后要计算每一行的和
end

%% (1)主成分聚类 ： 将主成分指标所在的F矩阵复制到Excel表格，然后再用Spss进行聚类
% 在Excel第一行输入指标名称（F1,F2, ..., Fm）
% 双击Matlab工作区的F,进入变量编辑中，然后复制里面的数据到Excel表格
% 导出数据之后，我们后续的分析就可以在Spss中进行。

%%（2）主成分回归：将x使用主成分得到主成分指标，并将y标准化，接着导出到Excel，然后再使用Stata回归
% Y = zscore(y);  % 一定要将y进行标准化哦~
% 在Excel第一行输入指标名称（Y,F1, F2, ..., Fm）
% 分别双击Matlab工作区的Y和F,进入变量编辑中，然后复制里面的数据到Excel表格
% 导出数据之后，我们后续的分析就可以在Stata中进行。





% % 注意：代码文件仅供参考，一定不要直接用于自己的数模论文中
% % 国赛对于论文的查重要求非常严格，代码雷同也算作抄袭
% % 视频中提到的附件可在售后群（购买后收到的那个无忧自动发货的短信中有加入方式）的群文件中下载。包括讲义、代码、我视频中推荐的资料等。
% % 关注我的微信公众号《数学建模学习交流》，后台发送“软件”两个字，可获得常见的建模软件下载方法；发送“数据”两个字，可获得建模数据的获取方法；发送“画图”两个字，可获得数学建模中常见的画图方法。另外，也可以看看公众号的历史文章，里面发布的都是对大家有帮助的技巧。
% % 购买更多优质精选的数学建模资料，可关注我的微信公众号《数学建模学习交流》，在后台发送“买”这个字即可进入店铺(我的微店地址：https://weidian.com/?userid=1372657210)进行购买。
% % 视频价格不贵，但价值很高。单人购买观看只需要58元，三人购买人均仅需46元，视频本身也是下载到本地观看的，所以请大家不要侵犯知识产权，对视频或者资料进行二次销售。
% % 如何修改代码避免查重的方法：https://www.bilibili.com/video/av59423231（必看）