雷达系统设计MATLAB仿真-雷达基础导论(1)

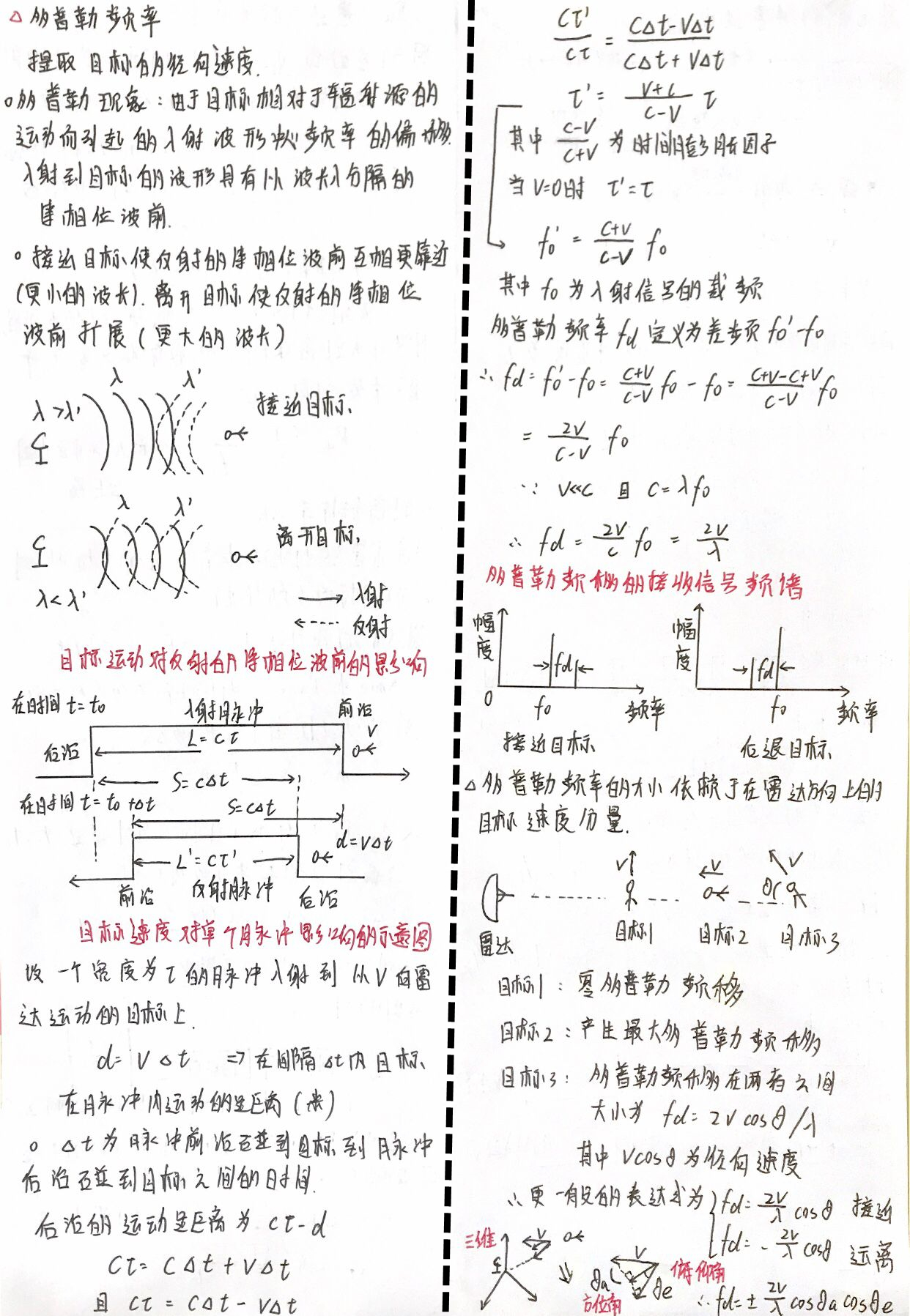

- 一般来说,以L表示的雷达损耗会降低总的SNR,所以:
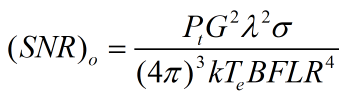
下面用MATLAB进行仿真
利用函数radar_eq.m 调用语法为:
[snr]=radar_eq(pt,freq,g,sigma,te,b,nf,loss,range)


函数“radar _eq.m”的设计使它对于输人“距离”,可以接受单个数值,或包含很多距离值的矢量。下图为一些典型曲线,这个程序使用了函数"radar _eq.m",默认输入如下:峰值功率Pt= 1.5 MW ,工作频率f0=5.6 GHz,天线增益G=45 dB,有效温度Te=290K,雷达损失L=6 dB,噪声系数F=3 dB。雷达带宽B=5 MHz。雷达最小和最大检测距离是Rmin = 25 km和Rmax = 165 km。假定目标截面积σ=0.1 m2。
- radar _eq.m代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | function[snr]=radar_eq(pt,freq,g,sigma,te,b,nf,loss,range)c=3.0e+8;%光速lambda=c/freq;%波长p_peak=10*log10(pt);%将峰值功率转化为分贝值dBlambda_sqdb=10*log10(lambda^2);%将波长的平方转化为分贝值dBsigmadb =10*log10(sigma); %将sigma转为dBfour_pi_cub = 10*log10((4.0*pi)^3); %将(4pi)^3转为dBk_db =10*log10(1.38e-23); % Boltzman's constant in dBte_db =10*log10(te); % noise temp. in dBb_db = 10*log10(b);% bandwidth in dBrange_pwr4_db =10*log10(range.^4);% vector of target range^4 in dB% Implement Equation 雷达距离方程num =p_peak +g+g+lambda_sqdb + sigmadb;den = four_pi_cub +k_db +te_db+b_db +nf + loss + range_pwr4_db;snr = num - den;return |
- 程序代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | close allclear allpt = 1.5e+6; % peak power in Wattsfreq = 5.6e+9; % radar operating frequency in Hzg = 45.0; % antenna gain in dBsigma = 0.1; % radar cross section in m squaredte = 290.0; % effective noise temperature in Kelvinsb = 5.0e+6;% radar operating bandwidth in Hznf = 3.0; %noise figure in dBloss = 6.0; % radar losses in dBrange = linspace(25e3,165e3,1000); % traget range 25 -165 Km,1000 pointssnr1 = radar_eq(pt, freq, g, sigma, te, b, nf, loss, range);snr2 = radar_eq(pt, freq, g, sigma/10, te, b, nf, loss, range);snr3 = radar_eq(pt, freq, g, sigma*10, te, b, nf, loss, range);% plot SNR versus rangefigure(1)rangekm = range./ 1000;%换算成KMplot(rangekm,snr3,'k',rangekm,snr1,'k -.', rangekm,snr2, 'k:')gridlegend('\sigma =0 dBsm', '\sigma =-10dBsm', '\sigma=-20 dBsm')xlabel('Detection range - Km');ylabel('SNR - dB');snr1 = radar_eq(pt, freq, g, sigma, te, b, nf, loss, range);snr2 = radar_eq(pt*.4, freq, g, sigma, te, b, nf, loss, range);snr3 = radar_eq(pt*1.8,freq, g, sigma, te, b, nf, loss, range);figure (2)plot(rangekm,snr3,'k',rangekm,snr1,'k -.', rangekm,snr2,'k:')gridlegend('Pt=2.16 MW','Pt=1.5 MW','Pt= 0.6MW')xlabel('Detection range - Km');ylabel('SNR - dB'); |
- 仿真图:
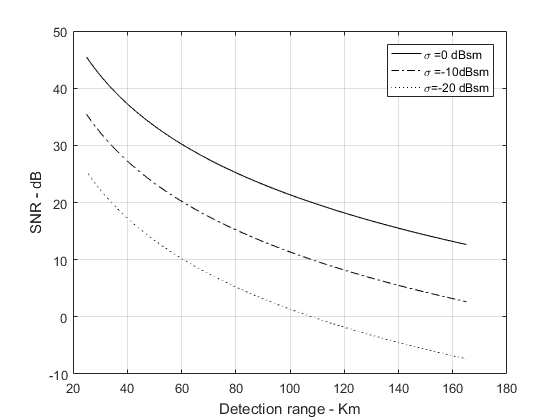
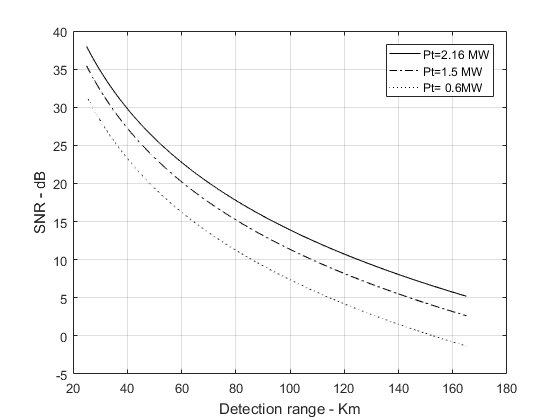
另一方面,也可以修改雷达方程来计算对于给定的检测距离为获得一定的SNR 所需要的脉冲宽度。在这种情况下,雷达方程可以写为
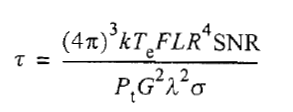
- 程序代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | % Use this program to reproduce Fig. 1.13 of text.close allclear allpt = 1.e+6; % peak power in Wattsfreq = 5.6e+9; % radar operating frequency in Hzg = 40.0; % antenna gain in dBsigma = 0.1; % radar cross section in m squaredte =300.0; % effective noise temperature in Kelvinsnf = 5.0; %noise figure in dBloss = 6.0; % radar losses in dBrange = [75e3,100e3,150e3]; % three range valuessnr_db = linspace(5,20,200); % SNR values from 5 dB to 20 dB 200 pointssnr = 10.^(0.1.*snr_db); % convert snr into base 10gain = 10^(0.1*g); %convert antenna gain into base 10loss = 10^(0.1*loss); % convert losses into base 10F = 10^(0.1*nf); % convert noise figure into base 10lambda = 3.e8 / freq; % compute wavelength% Implement Eq.(1.57)den = pt * gain * gain * sigma * lambda^2;num1 = (4*pi)^3 * 1.38e-23 * te * F * loss * range(1)^4 .* snr;num2 = (4*pi)^3 * 1.38e-23 * te * F * loss * range(2)^4 .* snr;num3 = (4*pi)^3 * 1.38e-23 * te * F * loss * range(3)^4 .* snr;tau1 = num1 ./ den ;tau2 = num2 ./ den;tau3 = num3 ./ den;% plot tau versus snrfigure(1)semilogy(snr_db,1e6*tau1,'k',snr_db,1e6*tau2,'k -.',snr_db,1e6*tau3,'k:')gridlegend('R = 75 Km','R = 100 Km','R = 150 Km')xlabel ('Minimum required SNR - dB');ylabel ('\tau (pulse width) in \mu sec'); |
- 仿真图:
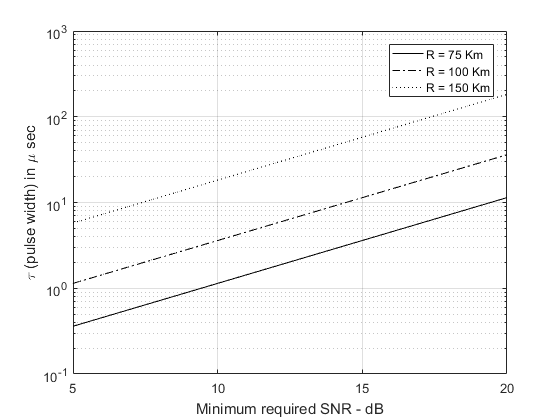
当进行雷达仿真时,脉冲宽度的选择是非常有用的。雷达系统经常使用有限数量的脉冲宽度(波形)来实现所有指定的工作模式。这些波形中的一些用来搜索和检测,另一些可能用于跟踪,同时有限数量的宽带波形可能用于分辨的目的。
雷达散射截面积(Radar Cross Section, RCS)
一旦计算了所要求的SNR,可以使用上图和对应的公式寻找最合适的脉冲(或波形)来获得所要求的SNR(或等效成所要求的PD)。对于在特定检测距离上的特定RCS数值,经常可能出现没有可用的雷达波形能够保证所要求的最小SNR的情况。在这种情况下,雷达必须一直等到目标在距离上足够接近时再建立起检测,另外就是使用脉冲积累(相干或非相干)。
- 雷达参考距离
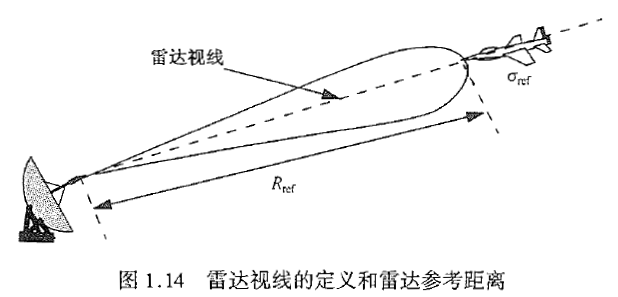
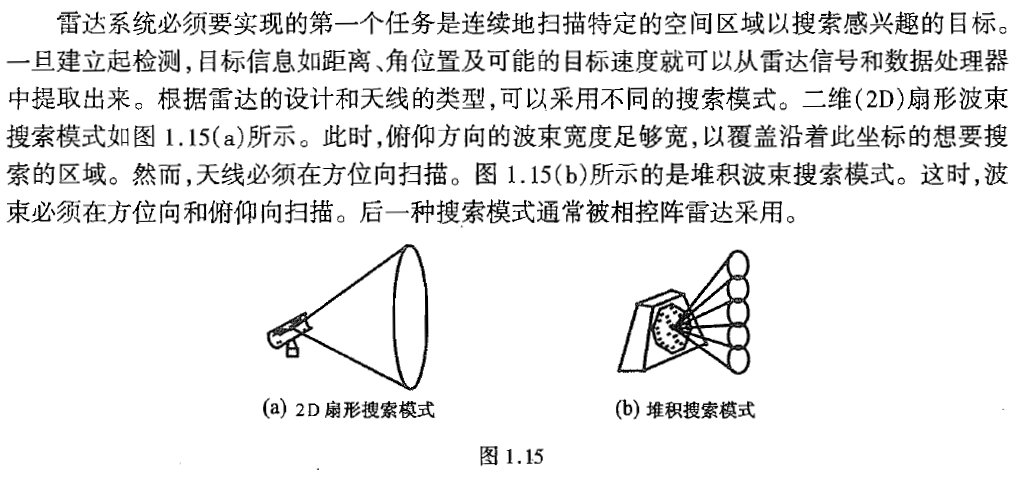
很多雷达设计问题可以根据雷达参考距离Rref推导或计算,其通常由雷达最终用户提供。它简单描述了这样一个距离,在此距离上,对于预先确定的目标截面积σref ,使用规定的参考脉冲宽度τref ,必须达到某个称为SNRref的SNR数值。雷达参考距离的计算假定目标位于天线波束内最大增益所定义的直线上(天线的法线)。这条直线通常称为雷达视线,如图1.14所示。
在参考距离上的雷达方程为:
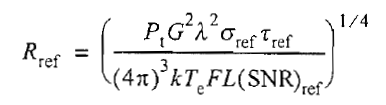
对SNR、RCS和脉冲宽度的任意其他组合,在任意其他探测距离上的雷达方程为
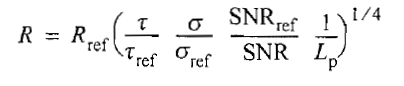
其中,附加的损失项Lp的引人是考虑到非参考目标可能不在雷达视线上,以及考虑到与特定场景相关的其他损失。上式的其他形式可以用SNR表示。更准确的表示为
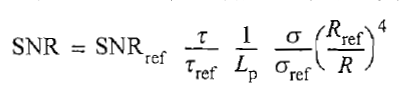
例如,考虑上―节描述的雷达,此时,定义σref = 0.1 m2,Rref = 86 km,以及 SNRref = 20 dB。参考脉冲宽度是τref =0.1 us。使用上式,对于RCS为σ = 0.2 m2,的目标,计算在R= 120 km处的SNR。假定Lp=2 dB相等,得到(SNR )120km = 15.2 dB。
计算过程为:
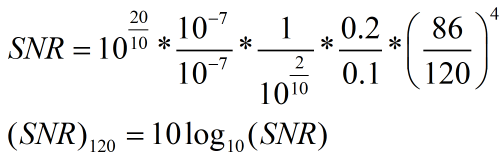
- 搜索(警戒)

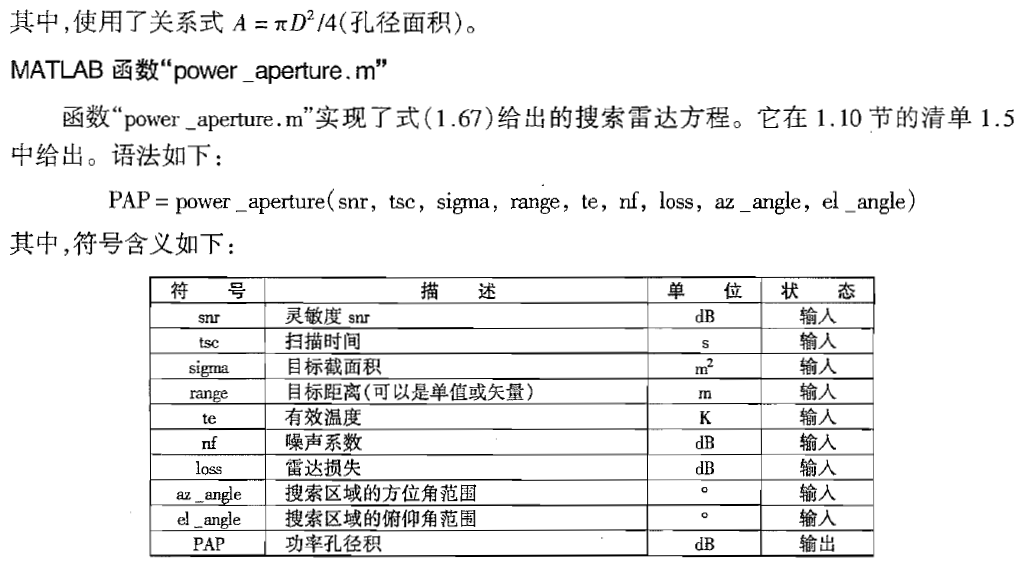
也就是对下面式子做仿真
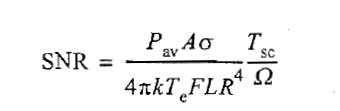
- power_aperture.m
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | function PAP = power_aperture(snr,tsc,sigma,range,te,nf,loss,az_angle,el_angle)% This program implements Eq. (1.67)Tsc = 10*log10(tsc); % convert Tsc into dBSigma = 10*log10(sigma); % convert sigma to dBfour_pi = 10*log10(4.0 * pi); % (4pi) in dBk_db = 10*log10(1.38e-23); % Boltzman's constant in dBTe = 10*log10(te); % noise temp. in dBrange_pwr4_db = 10*log10(range.^4); % target range^4 in dBomega = (az_angle/57.296) * (el_angle / 57.296); % compute search volume in steraradiansOmega = 10*log10(omega); % search volume in dB% implement Eq. (1.67)PAP = snr + four_pi + k_db + Te + nf + loss + range_pwr4_db + Omega ... - Sigma - Tsc;return |
- 仿真代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | % Use this program to reproduce Fig. 1.16 of text.close allclear alltsc = 2.5; % Scan time i s2.5 secondssigma = 0.1; % radar cross section in m sqauredte = 900.0; % effective noise temperature in Kelvinssnr = 15; % desired SNR in dBnf = 6.0; %noise figure in dBloss = 7.0; % radar losses in dBaz_angle = 2; % search volume azimuth extent in degreesel_angle = 2; %serach volume elevation extent in degreesrange = linspace(20e3,250e3,1000); % range to target from 20 Km 250 Km, 1000 pointspap1 = power_aperture(snr,tsc,sigma/10,range,te,nf,loss,az_angle,el_angle);pap2 = power_aperture(snr,tsc,sigma,range,te,nf,loss,az_angle,el_angle);pap3 = power_aperture(snr,tsc,sigma*10,range,te,nf,loss,az_angle,el_angle);% plot power aperture prodcut versus range% figure 1.16afigure(1)rangekm = range ./ 1000;plot(rangekm,pap1,'k',rangekm,pap2,'k -.',rangekm,pap3,'k:')gridlegend('\sigma = -20 dBsm','\sigma = -10dBsm','\sigma = 0 dBsm')xlabel ('Detection range in Km');ylabel ('Power aperture product in dB');% generate Figure 1.16blambda = 0.03; % wavelength in metersG = 45; % antenna gain in dBae = linspace(1,25,1000);% aperture size 1 to 25 meter squared, 1000 pointsAe = 10*log10(ae);range = 250e3; % rnage of interset is 250 Kmpap1 = power_aperture(snr,tsc,sigma/10,range,te,nf,loss,az_angle,el_angle);pap2 = power_aperture(snr,tsc,sigma,range,te,nf,loss,az_angle,el_angle);pap3 = power_aperture(snr,tsc,sigma*10,range,te,nf,loss,az_angle,el_angle);Pav1 = pap1 - Ae;Pav2 = pap2 - Ae;Pav3 = pap3 - Ae;figure(2)plot(ae,Pav1,'k',ae,Pav2,'k -.',ae,Pav3,'k:')gridxlabel('Aperture size in square meters')ylabel('Pav in dB')legend('\sigma = -20 dBsm','\sigma = -10dBsm','\sigma = 0 dBsm') |
- 仿真结果图
功率孔径积相对于检测距离
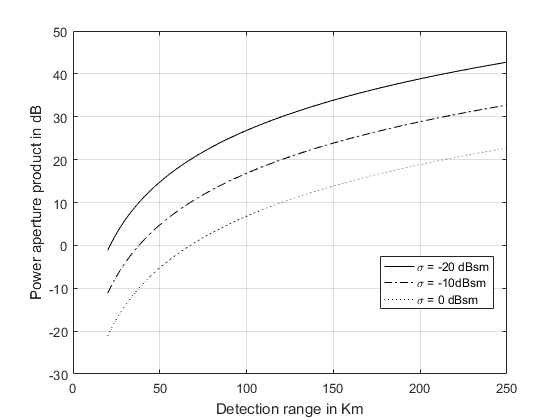
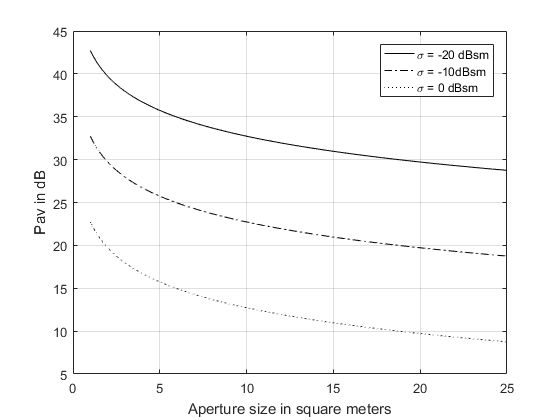
雷达平均功率相对于孔径大小
- 例题

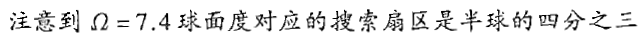
利用下图中的式子

可以算出
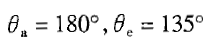
计算公式如下:
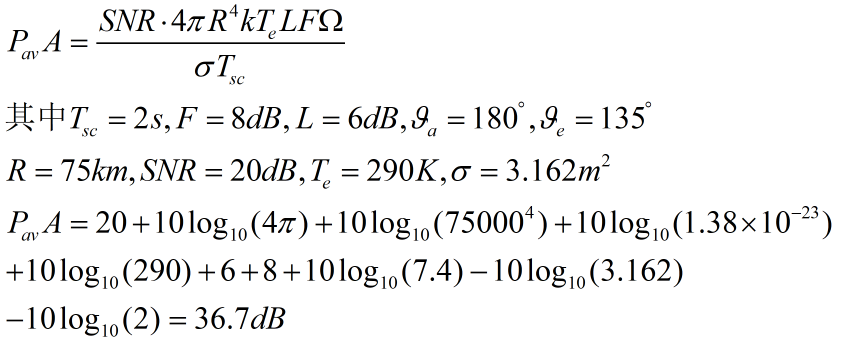

- 例题



其中1.8式为: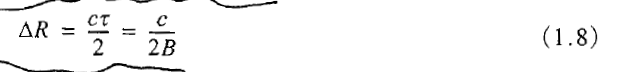

其中1.67式为:

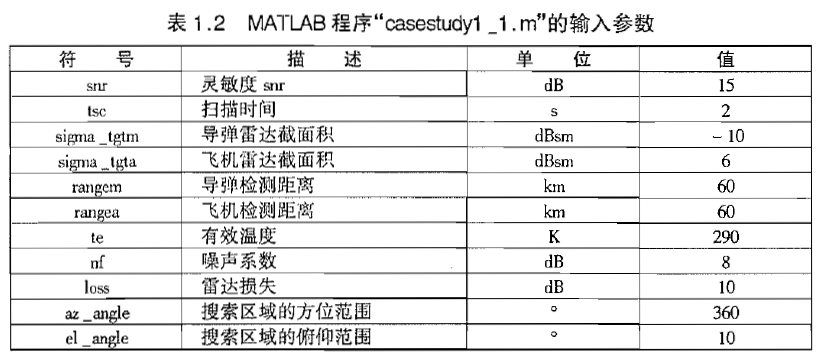
- 仿真代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | % This program is used to generate Fig. 1.17 % It implements the search radar equation defined in Eq. 1.67clear allclose allsnr = 15.0; % Sensitivity SNR in dBtsc = 2.; % Antenna scan time in secondssigma_tgtm = -10; % Missile RCS in dBsmsigma_tgta = 6; % Aircraft RCS in dBsmrange = 60.0; % Sensitivity range in Km, te = 290.0; % Effective noise temprature in Kelvinsnf = 8; % Noise figure in dBloss = 10.0; % Radar losses in dBaz_angle = 360.0; % Search volume azimuth extent in degreesel_angle = 10.0; % Search volume elevation extent in degreesc = 3.0e+8; % Speed of light% Compute Omega in steradiansomega = (az_angle / 57.296) * (el_angle /57.296);omega_db = 10.0*log10(omega); % Convert Omega to dBsk_db = 10.*log10(1.38e-23);te_db = 10*log10(te);tsc_db = 10*log10(tsc);factor = 10*log10(4*pi);rangemdb = 10*log10(range * 1000.);rangeadb = 10*log10(range * 1000.);PAP_Missile = snr - sigma_tgtm - tsc_db + factor + 4.0 * rangemdb + ... k_db + te_db + nf + loss + omega_dbPAP_Aircraft = snr - sigma_tgta - tsc_db + factor + 4.0 * rangeadb + ... k_db + te_db + nf + loss + omega_dbindex = 0;% vary rnage from 2Km to 90 Km for rangevar = 2 : 1 : 90 index = index + 1; rangedb = 10*log10(rangevar * 1000.0); papm(index) = snr - sigma_tgtm - tsc_db + factor + 4.0 * rangedb + ... k_db + te_db + nf + loss + omega_db; missile_PAP(index) = PAP_Missile; aircraft_PAP(index) = PAP_Aircraft; papa(index) = snr - sigma_tgta - tsc_db + factor + 4.0 * rangedb + ... k_db + te_db + nf + loss +omega_db;endvar = 2 : 1 : 90;figure (1)plot (var,papm,'k',var,papa,'k-.')legend ('Missile','Aircraft')xlabel ('Range - Km');ylabel ('Power Aperture Product - dB');hold onplot(var,missile_PAP,'k:',var,aircraft_PAP,'k:')gridhold off |
- 仿真图
雷达的功率孔径积相对检测距离
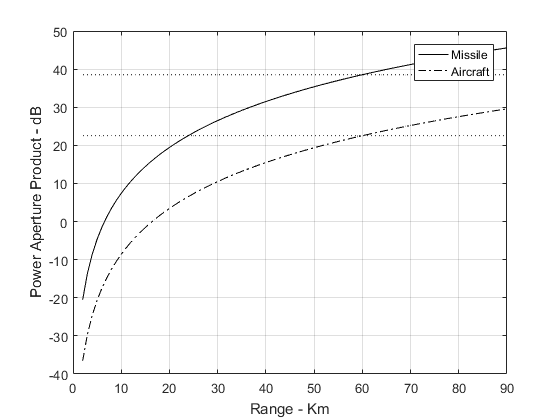
上图显示了这个程序产生的输出图形。这个同样的程序也计算了导弹和飞机对应的功率孔径积,它们也可以从这幅图上读出。

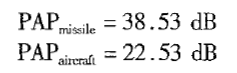

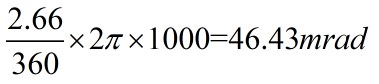



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具