MATLAB-Fourier变换

 

•  将振幅为1Hz的正弦波和振幅为0.5的5Hz正弦波相加后进行Fourier分析，研究能否从中分析出含有这两种频率的信号

clear all %清除所有变量
N=256;dt=0.02;  %数据的个数和采样间隔
n=0:N-1;t=n*dt; %序号序列和时间序列
x=sin(2*pi*t)+0.5*sin(2*pi*5*t);%合成的信号
m=floor(N/2)+1;%分解a,b的最大序列号，为分解的N/2个参数再加参数a0
%floor函数为向下取整
a=zeros(1,m);b=zeros(1,m);%产生a,b两个为0的序列
for k=0:m-1
    for ii=0:N-1
        a(k+1)=a(k+1)+2/N*x(ii+1)*cos(2*pi*k*ii/N);%求和
        b(k+1)=b(k+1)+2/N*x(ii+1)*sin(2*pi*k*ii/N);%求和
    end
    %数组下标只能从1开始
    c(k+1)=sqrt(a(k+1).^2+b(k+1).^2);%k次谐波的振幅大小
end
subplot(2,1,1),plot(t,x);title('原始信号');xlabel('时间/s');ylim([-1.5 1.5])
%绘出时间域信号
subplot(2,1,2),plot((0:m-1)/(N*dt),c);
%绘出频率域信号
title('Fourier变换');xlabel('频率/Hz'),ylabel('振幅')

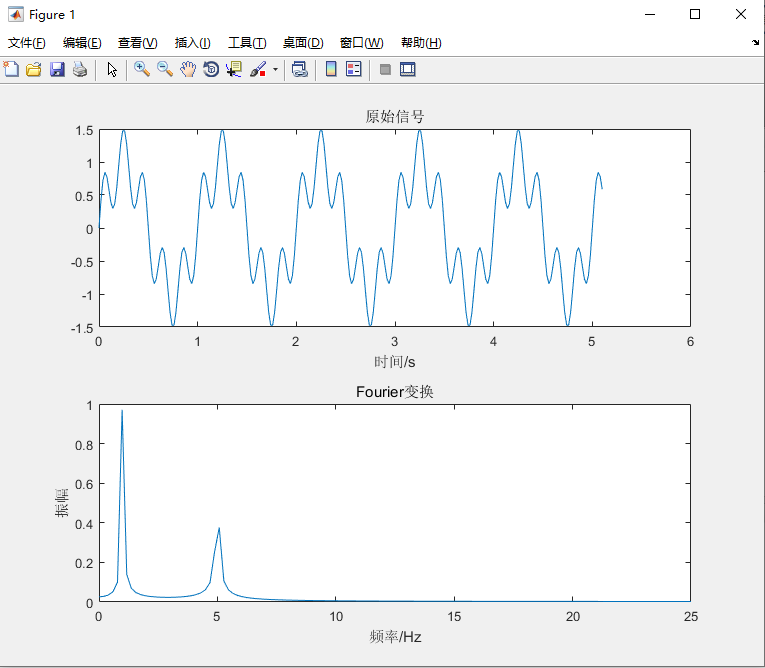
 可以看出Fourier变换识别出了1Hz和5Hz的波 与原信号不同是因为采样点数较少

• 将m改为N，增加镜像对称的部分

clear all %清除所有变量
N=256;dt=0.02;  %数据的个数和采样间隔
n=0:N-1;t=n*dt; %序号序列和时间序列
x=sin(2*pi*t)+0.5*sin(2*pi*5*t);%合成的信号
m=N;%镜像对称
%floor函数为向下取整
a=zeros(1,m);b=zeros(1,m);%产生a,b两个为0的序列
for k=0:m-1
    for ii=0:N-1
        a(k+1)=a(k+1)+2/N*x(ii+1)*cos(2*pi*k*ii/N);%求和
        b(k+1)=b(k+1)+2/N*x(ii+1)*sin(2*pi*k*ii/N);%求和
    end
    %数组下标只能从1开始
    c(k+1)=sqrt(a(k+1).^2+b(k+1).^2);%k次谐波的振幅大小
end
subplot(2,1,1),plot(t,x);title('原始信号');xlabel('时间/s');ylim([-1.5 1.5])
%绘出时间域信号
subplot(2,1,2),plot((0:m-1)/(N*dt),c);
%绘出频率域信号
title('Fourier变换');xlabel('频率/Hz'),ylabel('振幅')

        

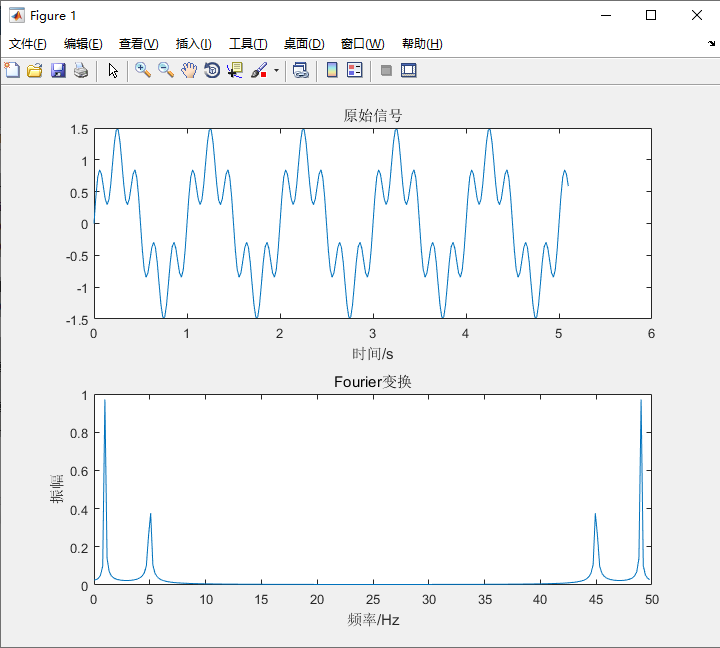
• m改为2N 频谱增加一个周期

clear all %清除所有变量
N=256;dt=0.02;  %数据的个数和采样间隔
n=0:N-1;t=n*dt; %序号序列和时间序列
x=sin(2*pi*t)+0.5*sin(2*pi*5*t);%合成的信号
m=2*N;%增加一个周期
%floor函数为向下取整
a=zeros(1,m);b=zeros(1,m);%产生a,b两个为0的序列
for k=0:m-1
    for ii=0:N-1
        a(k+1)=a(k+1)+2/N*x(ii+1)*cos(2*pi*k*ii/N);%求和
        b(k+1)=b(k+1)+2/N*x(ii+1)*sin(2*pi*k*ii/N);%求和
    end
    %数组下标只能从1开始
    c(k+1)=sqrt(a(k+1).^2+b(k+1).^2);%k次谐波的振幅大小
end
subplot(2,1,1),plot(t,x);title('原始信号');xlabel('时间/s');ylim([-1.5 1.5])
%绘出时间域信号
subplot(2,1,2),plot((0:m-1)/(N*dt),c);
%绘出频率域信号
title('Fourier变换');xlabel('频率/Hz'),ylabel('振幅')

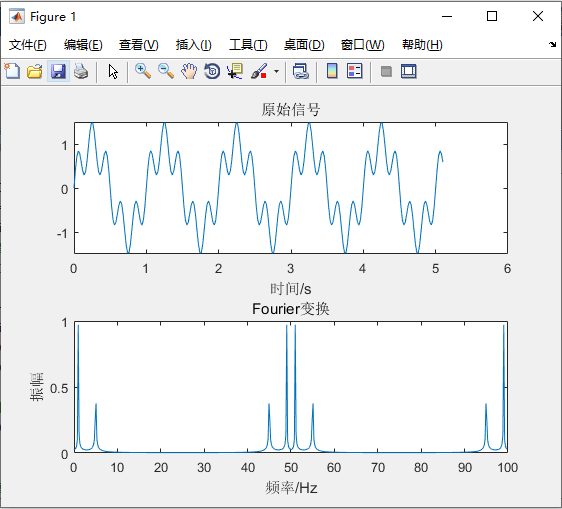
所以离散有限信号的频谱为周期谱

• 根据分解得到的ak,bk恢复原来的信号

clear all %清除所有变量
N=256;dt=0.02;  %数据的个数和采样间隔
n=0:N-1;t=n*dt; %序号序列和时间序列
x=sin(2*pi*t)+0.5*sin(2*pi*5*t);%合成的信号
m=floor(N/2)+1;%增加一个周期
%floor函数为向下取整
a=zeros(1,m);b=zeros(1,m);%产生a,b两个为0的序列
for k=0:m-1
    for ii=0:N-1
        a(k+1)=a(k+1)+2/N*x(ii+1)*cos(2*pi*k*ii/N);%求和
        b(k+1)=b(k+1)+2/N*x(ii+1)*sin(2*pi*k*ii/N);%求和
    end
    %数组下标只能从1开始
    c(k+1)=sqrt(a(k+1).^2+b(k+1).^2);%k次谐波的振幅大小
end

if(mod(N,2)~=1)
    a(m)=a(m)/2;
end
%也就是N为偶数的时候 b(m)为0,a(m)减半
for ii=0:N-1
    xx(ii+1)=a(1)/2;
    for k=1:m-1
        xx(ii+1)=xx(ii+1)+a(k+1)*cos(2*pi*k*ii/N)+b(k+1)*sin(2*pi*k*ii/N);%求和
    end
end
subplot(2,1,1)
plot((0:N-1)*dt,x)%绘制原始信号
title('原始信号')
ylim([-2,2])
subplot(2,1,2)
plot((0:N-1)*dt,xx)%绘制合成信号
title('合成信号')
xlabel('时间/s')
ylim([-2,2])