从2-3-4树模型到红黑树实现
从2-3-4树模型到红黑树实现
前言
红黑树,是一个高效的二叉查找树。其定义特性保证了树的路径长度在黑色节点上完美平衡,使得其查找效率接近于完美平衡的二叉树。
但是红黑树的实现逻辑很复杂,各种旋转,颜色变化,直接针对其分析,大多数都是死记硬背各种例子,不太容易有个直观的理解。实际上,红黑树是实现手段,是其他概念模型为了方便在二叉树上实现进而定义的节点颜色这个信息。如果从概念模型入手,再一一对应,就容易理解的多了。而红黑树能够对应的模型有2-3树,2-3-4树等,下面我们会以2-3-4树作为概念模型,对红黑树进行分析。
2-3-4树
2-3-4树是对完美平衡二叉树的扩展,其定义为:
- 在一个节点中,可以存在1-3个
key。 - 2-节点,拥有1个
key和2个子节点。 - 3-节点,拥有2个
key和3个子节点。 - 4-节点,拥有3个
key和4个子节点。 - 子节点为空的节点称为叶子节点。
- 任意从根节点到叶子节点的路径拥有相同的长度,即路径上的链接数相同。
下图就是一个2-3-4树:

查找
2-3-4树的查找很简单,类似于二叉树,步骤如下:
- 将查找
key和节点内的key逐一对比。 - 如果命中,则返回节点内
key的对应值。 - 如果节点内的
key都不命中,则沿着合适的链接到下一节点重复该过程直到找到或者无后续节点。
举个例子,如果我们要在上面的2-3-4树中查询11,其步骤如下:


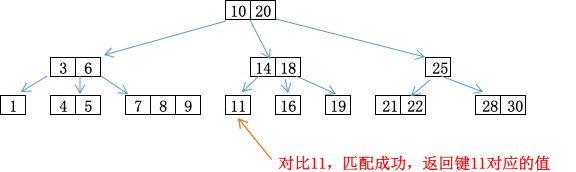
插入
2-3-4树的插入,不会发生在中间节点,只会在叶子节点上进行插入。

 、
、
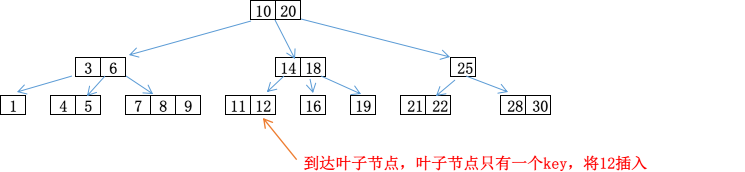
在叶子节点上新增key,会使得2-节点变为3-节点,3-节点变为4-节点。而原本的4-节点就没有空间可以插入key了。为了解决这个问题,可以将4-节点中间的key推送给其父节点,剩下的2个key形成2个2-节点。效果如下



通过将4-的叶子节点拆分,产生了新的叶子节点可供key插入,同时将中间key送入父节点。该操作不会破坏树的平衡性和高度。但如果叶子节点的父节点也是4-节点,这个操作就无法进行了。为了解决这个问题,有两种思路:
- 自底向上,从4-叶子节点开始分裂,如果分类后其父节点也是4-节点,继续向上分裂,直到到达根节点。如果根节点也是4-节点,分裂后树的高度+1。
- 自顶向下,从根节点到插入所在的叶子节点路径上,遇到4-节点就将其分裂。
两种方法都能解决问题,不过自顶向下不需要递归,实现起来更简单。通过这种处理方式,确保了1)最后到达的叶子节点必然是2-或者3-节点,搜索路径上不存在4-节点。
树的生长
2-3-4树是向上生长的。这句话可以从根节点的分裂理解:如果根节点是一个4-节点,当新增key时,根节点会分裂,将中间的key推入父节点。根节点没有父节点,因此中间的key就会成为新的根节点。如下所示:

整颗树的生长可以看成是叶子节点不断的新增key,并且在成为4-节点后被下一次的新增动作分解为2个2-节点,同时将一个key送入父节点。随着这个过程的不断进行,不断有key从叶子节点向根节点汇聚,直到根节点成为4-节点并在下一次新增时被分类,进而让树升高1。
删除
删除是整个操作中最为复杂的部分,因为删除可能发生在任意节点上,并且删除后可能破坏2-3-4树的完美平衡。在这里,我们先来处理一些简单的情况,最后再思考可以推而广之的策略。
删除最大key
在2-3-4树中,删除最大key必然是最右边的叶子节点上。如果叶子节点是3-节点或者4-节点,只需要将其中最大的key删除即可,不会对树的平衡性造成影响。但如果删除的key在2-节点上,情况就变得麻烦,因为删除2-节点,导致树的平衡被破坏。为了避免这个情况的发生,不能让删除发生在2-节点上。
为了让删除不落在2-节点上,可以将2-类型的叶子节点(最终要删除的那个),从其兄弟节点“借”一个key进行融合变成3-节点;也可以将父节点的key和兄弟节点的key融合,变成一个4-节点,主要保证变化过程中树的平衡性不被破坏即可。变换完成之后的节点类型是3-或4-,自然就可以成功删除了。变化的可能情况有:

变化的策略是:
- 将父节点的
key,自身的key,兄弟节点的key的合并后形成一个逻辑节点。 - 变化一:新节点为4-节点的情况下,父节点还有key,则新节点替换目标节点;
- 变化二:新节点为5-节点的情况下,最小
key还给兄弟节点,次小key还给父节点,剩余2个key设置到目标节点。 - 变化三:新节点为6-节点的情况下,最小
key还给兄弟节点,次小key还给父节点,剩余3个key设置到目标节点。
向下的搜索,最终达到需要删除key的叶子节点。叶子节点的兄弟节点无法控制,而如果能保证目标key所在的叶子节点的父节点不是2-节点,就可以安全删除key而不会破坏树的结构。因此,在自顶向下的过程中,非根节点如果为2-节点,则通过变化成为非2-节点。这个转化,仅仅针对搜索路径的下一个节点而言,因此可能出现节点1被转化为非2-节点后,其子节点是2-节点,子节点转化为非2-节点时将父节点(节点1)恢复成2-节点。转化的最终目的是为了保证叶子节点的父节点是非2-节点即可,只不过为了达成这个保证,整个转化行为需要从根节点一直进行下去。因此如果在叶子节点的时候执行转化可能会导致子树高度减1,这种变化会影响到全局树的平衡。就需要循环向上迭代到根节点,比较复杂。而从根节点开始一路转化下去,则容易理解和实现,也不会影响树的平衡。
通过执行这种变化,在叶子节点中,就可以安全删除key。
删除最小key
最小key的删除思路和操作方式和删除最大key相似,只不过搜索路径的方向是最左而已,其节点变化策略也是相似的,具体的变化有以下几种:
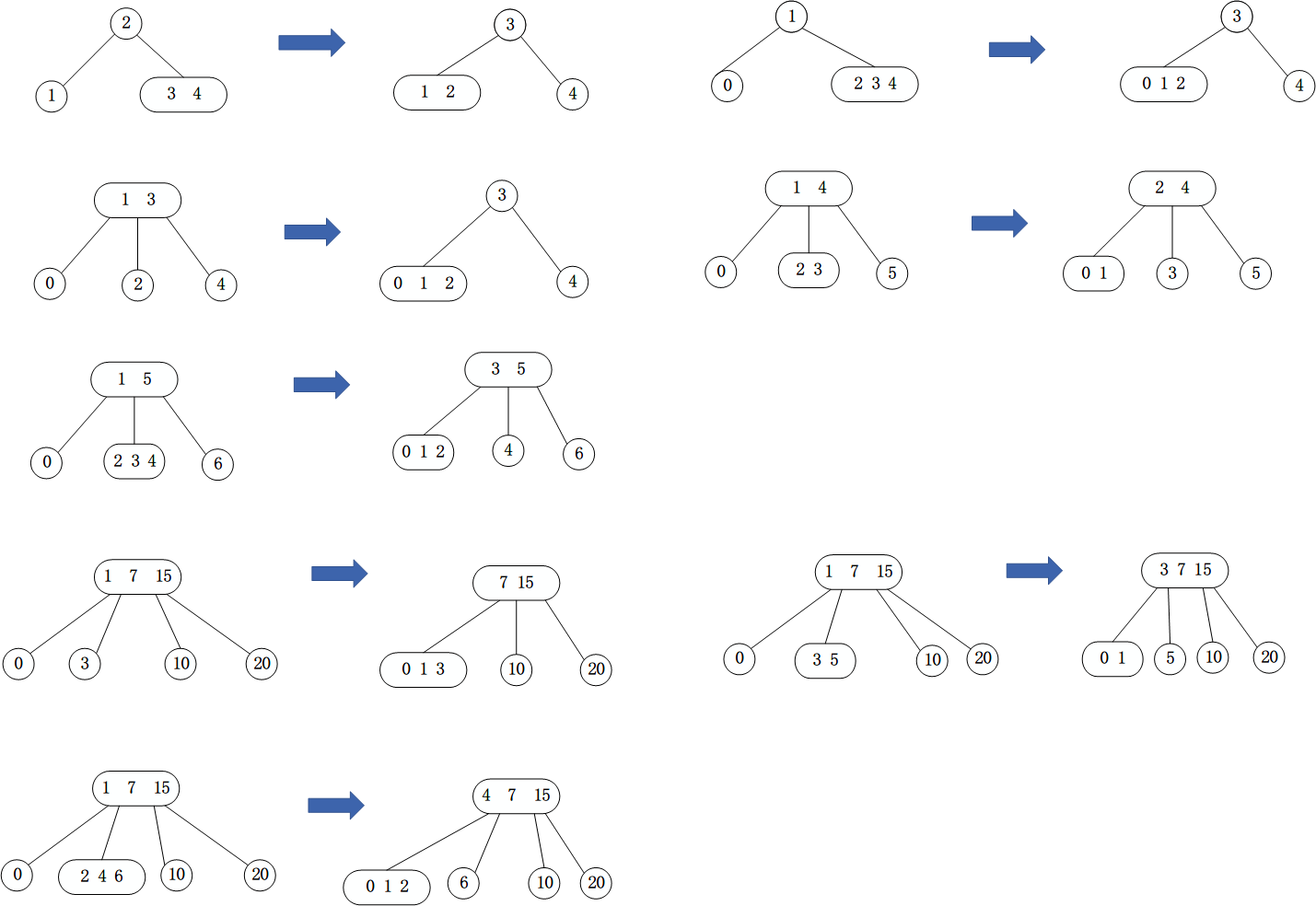
变化的策略是:
- 将父节点的
key,自身的key,兄弟节点的key的合并后形成一个逻辑节点。 - 变化一:新节点为4-节点的情况下,父节点还有key,则新节点替换目标节点;
- 变化二:新节点为5-节点的情况下,最大
key还给兄弟节点,次大key还给父节点,剩余2个key设置到目标节点。 - 变化三:新节点为6-节点的情况下,最大
key还给兄弟节点,次大key还给父节点,剩余3个key设置到目标节点。
删除任意key
删除任一key就变得比较麻烦,key可能出现在中间节点上,删除的话,树的结构就被破坏了。这里,我们可以采用一个取巧的思路:如果删除的key是树的中间节点,将该key替换为其中序遍历的后继key;该后继key是删除key的节点的右子树的最小key。
key的替换对树无影响;而将替换key删除,则转换为删除对应子树最小Key的问。删除最小Key,需要从根节点自顶向下变化2-节点才能保证叶子节点中key的成功删除。因此,删除任一Key的具体处理思路可以总结为:
- 从根节点开始自顶向下搜索,非根节点如果为2-节点,则通过变化成为非2-节点。
- 搜索发现目标key,将其替换为中序搜索后继key。
- 删除步骤2节点的右子树最小key。
左倾红黑树
2-3-4树是一种概念模型,直接按照这个概念模型用代码实现则比较复杂,主要的复杂有:
- 维持3种节点类型。
- 多种节点类型之间需要互相转换。
- 在树中移动需要进行多次比较,如果节点不是2-节点的话。
因此在表现形式上,我们将2-3-4树换另外一种形式来展现,进行以下变换:
- 将2-3-4树用二叉树的形式表现。
- 节点之间的链接区分为红色和黑色。红色链接用于将节点链接起来视作3-节点和4-节点。

这种转换的关键点在于:
- 转换后的二叉树可以使用二叉树的搜索方式。
- 转换后的二叉树和2-3-4树处于一致关系,改变的只是表现形式。
不过由于3-节点两种表现形式,增大了复杂性,因此对变换要求增加一条:红色链接只能为左连接。通过三个约束后,转换得到二叉树我们称之为左倾斜红黑树,其关键特性有:
- 可以使用二叉树搜索方式。
- 与2-3-4树保持一一对应。
- 红黑树是黑色链接完美平衡的,也就是从根节点到叶子节点的任意路径上,黑色链接的数量一致。
其对应方式如下:

可以看到,如果将红色链接放平,就和2-3-4树在展现上一致了。2-3-4树是完美平衡的,其对应的左倾斜红黑树是黑色链接完美平衡,因为红色链接是用于3-节点和4-节点的;而黑色链接就对应2-3-4树中的链接。
左倾斜红黑树的转换中不允许2种形式:
- 右倾斜的红色链接。
- 两个连续的红链接在一个搜索路径中(从根到叶子节点的路径)
形象的说以下几种不允许:

禁止的情况,减少了需要考虑的情形,为后续的编码实现降低了难度。对于上述定义的左倾斜红黑树,使用数据结构来表达的话,在原本的二叉树的节点中,增加一个属性color,用于表示指向该节点的链接的颜色。
public class RedBlackTree
{
private static final boolean RED = true;
private static final boolean BLACK = false;
private Node root; // root of the BST
private int heightBLACK; // black height of tree
private class Node
{
`key` `key`; // `key`
Value value; // associated data
Node left, right; // left and right subtrees
boolean color; // color of parent link
private int N; // number of nodes in tree rooted here
private int height; // height of tree rooted here
Node(`key` `key`, Value value)
{
this.`key` = `key`;
this.value = value;
this.color = RED;
this.N = 1;
this.height = 1;
}
}
}
查找
红黑树的查找和二叉树的一致,但是会更加快速,因为红黑树是黑色平衡的,搜索长度得到了控制。
插入
在介绍插入实现之前,首先要介绍红黑树中的两种旋转操作:
- 右旋:将一个左倾斜的红链接转化为右链接。
- 左旋:将一个右倾斜的红链接转化为左连接。
这两个操作的重要性在于其变化是局部的,不影响黑色连接的平衡性。其变化如下:

红黑树的插入和二叉树插入是相同的,只不过新增的链接是红色的。因为红黑树的概念模型是2-3-4树,2-3-4树新增节点是在叶子节点上,并且新增后必然成为3-节点或者4-节点,所以新增链接均为红色。
在新增完毕后,根据红链接具体情况,进行旋转处理,以保持左倾斜红黑树的要求。可能出现的情况有:
- 在2-节点上新增
key,表现在红黑树上,就是一个黑色的节点新增左连接或者右连接 - 在3-节点上新增
key,表现在红黑树上,就是被红链接相连的两个节点上3个可新增连接的地方新增红链接。
2-节点的情况如下所示:
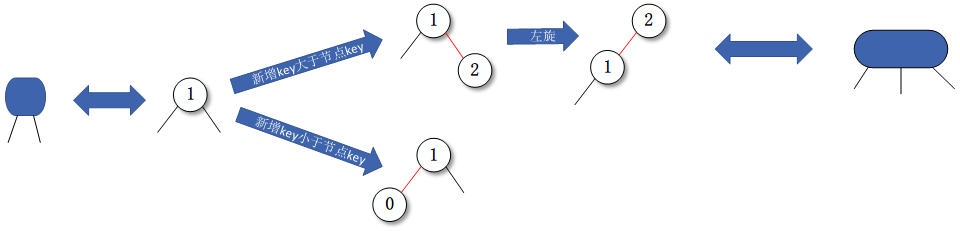
3-节点的情况如下所示:

左旋和右旋的方法如下:
private Node rotateLeft(Node h)//将节点的右红链接转化为左链接,并且返回原本节点的子树转化后新的子树的根节点
{
Node x = h.right;
h.right = x.left;
x.left = setN(h);
x.color = x.left.color;
x.left.color = RED;
return setN(x);//该方法用于计算节点x的子树内的节点数量以及高度
}
private Node rotateRight(Node h)//将节点的左红链接转化为右链接,并且返回原本节点的子树转化后新的子树的根节点
{
Node x = h.left;
h.left = x.right;
x.right = setN(h);
x.color = x.right.color;
x.right.color = RED;
return setN(x);
}
在2-3-4树的节点插入中,为了避免叶子节点是4-节点导致没有空间插入,所以从根节点到叶子节点的搜索路径中,采用自顶向下的4-节点分解策略。而在红黑树中,对4-节点的分解动作是通过对节点的颜色变化完成的,如下图所示:

翻转的过程很简单,就是将节点,节点的左右孩子节点的颜色都进行调整即可,颜色翻转的代码如下
private void colorFlip(Node h)
{
h.color = !h.color;
h.left.color = !h.left.color;
h.right.color = !h.right.color;
}
4-节点的分解带来的效果是将红色链接向上层移动,这个移动可能产生一个红色的右链接,此时需要通过左旋来修正;或者产生2个连续的红链接,此时需要将其右旋,形成一个符合定义的4-节点。
总结来说,插入的过程首先是自顶向下,遇到4-节点就进行分解,直到到达叶子节点插入新的key;由于向下过程的4-节点可能产生右倾斜的红链接,或者连续的2个红链接,因此需要从叶子节点处向上到达根节点,修复产生的这些问题。处理方式主要是:
- 右倾斜的红链接左旋。
- 连续的红链接,通过右旋来达到符合定义的4-节点。
按照上述的总结,我们可以将新增节点的方法实现为
private Node insert(Node h, `key` `key`, Value value)//将KV对插入以h节点为根节点的树,并且返回插入后该树的根节点
{
if (h == null)//寻找到空白链接,返回新的节点。该节点为红色链接指向的节点。
{
return new Node(`key`, value);
}
if (isRed(h.left) && isRed(h.right))//自顶向下的过程中,分裂4-节点。
{
colorFlip(h);
}
if (eq(`key`, h.`key`))
{
h.value = value;
}
else if (less(`key`, h.`key`))
{
h.left = insert(h.left, `key`, value);
}
else
{
h.right = insert(h.right, `key`, value);
}
if (isRed(h.right))//右倾斜的红色链接,进行左旋。
{
h = rotateLeft(h);
}
if (isRed(h.left) && isRed(h.left.left))//连续的红色链接,右旋变化为符合定义的4-节点
{
h = rotateRight(h);
}
return setN(h);
}
删除
和概念模型相同的方法,我们首先尝试实现删除最大key和删除最小key,之后通过替换key位置来实现删除任意Key功能。
删除最大Key
和概念模型相同,删除要发生在非2-节点上才能保证树的平衡不被破坏。这就意味着删除一定要发生在一个被红色链接相连的节点上。概念模型当中,在自顶向下搜索过程需要保证中间节点不是2-节点来使得叶子节点必然可以转化为非2-节点进行安全删除;反应在红黑树中,搜索路径的下一个节点,必须要被红色链接相连。如果不是的话,则要进行变化,具体的手段包括:
- 当前节点有左倾斜红色链接时,将其进行右旋。右旋可以从概念模型上理解,可以认为搜索路径是进行到3-节点或4-节点,并且从小
key搜索到大key。 - 搜索路径的下一节点为2-节点,转化为非-2节点。这个转化过程,参考概念模型中的做法,将当前节点的
key,右子节点的key,左子节点的key先合并,产生红链接相连的逻辑节点。之后按照概念模型的拆分方式进行拆分。
针对步骤二,我们做下具体的分析。
当前节点不是2-节点,且3-节点的红色左连接被转化为右链接,因此在下一个节点为2-节点的情况下,当前节点必然是被右倾斜红链接指向。所示初始状态可能如下:
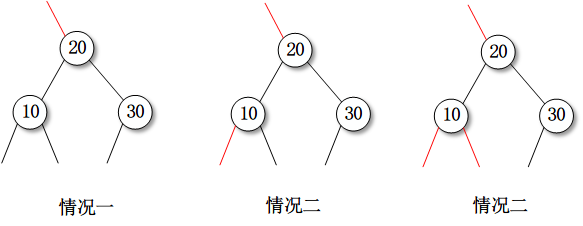
对于情况一,我们只需要对节点20进行颜色翻转,就可以让其后继节点变为红色,也就是链接变红,即可。这种转换对应概念模型中的变化1。
对于情况二,比较复杂。首先我们需要对节点20进行颜色翻转。此时节点10和20在一行路径上,对节点20的左连接右旋,右旋之后节点10变为新的根节点,对齐进行颜色翻转。整个过程如下

这种转换对应概念模型中的变化2。
情况三和情况二可以采用完全相同的变化步骤,转换方式对应概念模型中的变化3。如下图所示:

综合情况一、二、三,我们可以将变换的代码撰写为
private Node moveRedRight(Node h)
{
colorFlip(h);//先翻转
if (isRed(h.left.left))//此时为情况二或者三
{
h = rotateRight(h);
colorFlip(h);
}
return h;
}
结合红链接右旋和转换2-节点,我们可以将删除最大key的代码编写如下:
public void deleteMax()
{
root = deleteMax(root);
root.color = BLACK;//如果根节点右子节点为2-节点,翻转root节点会导致其颜色变红,不符合定义。因此删除完成后,将颜色恢复为颜色。
}
private Node deleteMax(Node h)//删除h节点为根节点的子树中的最大节点,并且返回删除后的子树的根节点
{
if (isRed(h.left))
{
h = rotateRight(h);
}
if (h.right == null)//没有右子树了,删除该节点
{
return null;
}
if (!isRed(h.right) && !isRed(h.right.left))//右子节点为2-节点,进行变化过程。
{
h = moveRedRight(h);
}
h.right = deleteMax(h.right);
return fixUp(h);
}
private Node fixUp(Node h) //修正可能存在的异常链接情况。
{
if (isRed(h.right))
{
h = rotateLeft(h);
}
if (isRed(h.left) && isRed(h.left.left))
{
h = rotateRight(h);
}
if (isRed(h.left) && isRed(h.right))
{
colorFlip(h);
}
return setN(h);
}
这个实现中引入了一个之前未曾提到的方法fixUp。因为在删除的过程自顶向下的变换会产生一些不符合定义的链接情况:比如右倾斜的红链接,比如连续的红链接。在删除完毕后,需要沿着之前的搜索路径,自底向上,进行异常链接修复。
删除最小Key
删除最小Key的思路和删除最大Key的思路非常接近,只不过在于搜索的方向不同,是沿着左子节点一直向下搜索。相比于删除最大Key,删除最小Key在搜索路径向下的过程中不需要对红链接方向进行旋转,当搜索路径的下一节点存在2-节点时转化为非2-节点。可能存在的初始情况如下图:
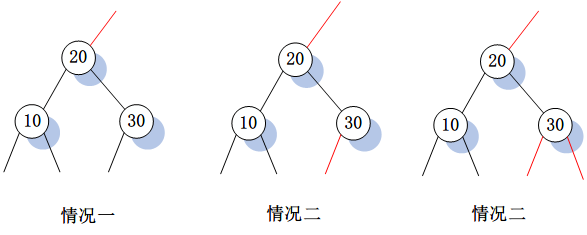
情况一很简单,只需要对节点20进行颜色翻转。该变换对应概念树中的变化1。
对于情况二,先对节点20进行翻转,再对节点30的左连接右旋,再对节点20的右链接左旋,最后对顶点进行翻转。流程如下图所示:

该变换对应概念模型中的变化2。
对于情况三则更复杂一些,其对应概念模型中的变化3,流程如下

和删除最大key不同的地方在于情况三无法复用情况2的操作,否则会产生一个右倾斜的红链接。不过即使是右倾斜红链接,仍然是黑色平衡。但是与左倾斜红黑树定义不吻合,所以情况三使用了更多的步骤来产生符合定义的红黑树。
结合上述过程,我们可以将删除最小Key的代码编写如下
public void deleteMin()
{
root = deleteMin(root);
root.color = BLACK;
}
private Node deleteMin(Node h)
{
if (h.left == null)
{
return null;
}
if (!isRed(h.left) && !isRed(h.left.left))
{
h = moveRedLeft(h);
}
h.left = deleteMin(h.left);
return fixUp(h);
}
private Node moveRedLeft(Node h)
{
colorFlip(h);
if (isRed(h.right.left))
{
if (isRed(h.right.right))
{
h.right = rotateRight(h.right);
h = rotateLeft(h);
h = rotateLeft(h);
h.left = rotateRight(h.left);
colorFlip(h);
}
else
{
h.right = rotateRight(h.right);
h = rotateLeft(h);
colorFlip(h);
}
}
return h;
}
删除任意Key
和概念模型的删除操作相似,自顶向下搜索,按照key的比较结果,可能向左右任意方向前进,如果下一步是一个2-节点,则参照删除最大最小key中的变化方式进行变化。在确定key所在的节点后,将该key值替换为中序遍历的后继节点,继而删除该节点右子树的最小节点。代码如下
public void delete(Key key)
{
root = delete(root, key);
root.color = BLACK;
}
private Node delete(Node h, Key key)
{
if (less(key, h.key))
{
if (!isRed(h.left) && !isRed(h.left.left))
{
h = moveRedLeft(h);
}
h.left = delete(h.left, key);
}
else
{
if (isRed(h.left))
{
h = rotateRight(h);
}
if (eq(key, h.key) && (h.right == null))
{
return null;
}
if (!isRed(h.right) && !isRed(h.right.left))
{
h = moveRedRight(h);
}
if (eq(key, h.key))
{
h.value = get(h.right, min(h.right));
h.key = min(h.right);
h.right = deleteMin(h.right);
}
else
{
h.right = delete(h.right, key);
}
}
return fixUp(h);
}
总结
红黑树作为概念树的实际实现,其代码很复杂,要求的变化方式也很多。从概念树的映射来说,2-3树,2-3-4树都可以映射到红黑树上。而左倾斜红黑树,使用递归方式实现的代码,无疑是很好理解,代码量也较少的。而JDK中TreeMap采用概念模型也是2-3-4树,不过并不限制右倾斜。总体而言,红黑树有太多变种,了解其原理最为重要,实现上,能使用即可,深究的话,意义不大。
参考文献
《Left-Leaning Red-Black Trees》(Princeton University)
文章原创首发于公众号:林斌说Java,转载请注明来源,谢谢。
更多高质量原创文章,欢迎扫码关注



 浙公网安备 33010602011771号
浙公网安备 33010602011771号