Python机器学习——Agglomerative层次聚类

层次聚类（hierarchical clustering）可在不同层次上对数据集进行划分，形成树状的聚类结构。AggregativeClustering是一种常用的层次聚类算法。 
  其原理是：最初将每个对象看成一个簇，然后将这些簇根据某种规则被一步步合并，就这样不断合并直到达到预设的簇类个数。这里的关键在于：如何计算聚类簇之间的距离？ 
  由于每个簇就是一个集合，因此需要给出集合之间的距离。给定聚类簇Ci,CjCi,Cj，有如下三种距离：

  • 最小距离：
     
    dmin(Ci,Cj)=minx⃗ i∈Ci,x⃗ j∈Cjdistance(x⃗ i,x⃗ j)dmin(Ci,Cj)=minx→i∈Ci,x→j∈Cjdistance(x→i,x→j)
    它是两个簇的样本对之间距离的最小值。
  • 最大距离：
     
    dmax(Ci,Cj)=maxx⃗ i∈Ci,x⃗ j∈Cjdistance(x⃗ i,x⃗ j)dmax(Ci,Cj)=maxx→i∈Ci,x→j∈Cjdistance(x→i,x→j)
    它是两个簇的样本对之间距离的最大值。
  • 平均距离：
     
    davg(Ci,Cj)=1|Ci||Cj|∑x⃗ i∈Ci∑x⃗ j∈Cjdistance(x⃗ i,x⃗ j)davg(Ci,Cj)=1|Ci||Cj|∑x→i∈Ci∑x→j∈Cjdistance(x→i,x→j)
    它是两个簇的样本对之间距离的平均值。

  当该算法的聚类簇采用dmindmin时，称为单链接single-linkage算法，当该算法的聚类簇采用dmaxdmax时，称为单链接complete-linkage算法，当该算法的聚类簇采用davgdavg时，称为单链接average-linkage算法。

  下面给出算法：

  • 输入： 
    • 数据集D=D={x⃗ 1,x⃗ 2,...,x⃗ Nx→1,x→2,...,x→N}
    • 聚类簇距离度量函数
    • 聚类簇数量KK
  • 输出：簇划分C=C={C1,C2,...,CKC1,C2,...,CK}

  • 算法步骤如下：

    • 初始化：将每个样本都作为一个簇
       
      Ci=[x⃗ i],i=1,2,...,NCi=[x→i],i=1,2,...,N
    • 迭代：终止条件为聚类簇的数量为K。迭代过程如下： 
      • 计算聚类簇之间的距离，找出距离最近的两个簇，将这两个簇合并。 

     

    Python实战

     

      AgglomerativeClustering是scikit-learn提供的层级聚类算法模型，其原型为：

class sklearn.cluster.AgglomerativeClustering(n_clusters=2, affinity=’euclidean’, memory=None, connectivity=None, compute_full_tree=’auto’, linkage=’ward’, pooling_func=<function mean>)
  • 1

参数

  • n_clusters：一个整数，指定分类簇的数量
  • connectivity：一个数组或者可调用对象或者None，用于指定连接矩阵
  • affinity：一个字符串或者可调用对象，用于计算距离。可以为：’euclidean’，’l1’，’l2’，’mantattan’，’cosine’，’precomputed’，如果linkage=’ward’，则affinity必须为’euclidean’
  • memory：用于缓存输出的结果，默认为不缓存
  • n_components：在 v-0.18中移除
  • compute_full_tree：通常当训练了n_clusters后，训练过程就会停止，但是如果compute_full_tree=True，则会继续训练从而生成一颗完整的树
  • linkage：一个字符串，用于指定链接算法 
    • ‘ward’：单链接single-linkage，采用dmindmin
    • ‘complete’：全链接complete-linkage算法，采用dmaxdmax
    • ‘average’：均连接average-linkage算法，采用davgdavg
  • pooling_func：一个可调用对象，它的输入是一组特征的值，输出是一个数

属性

  • labels：每个样本的簇标记
  • n_leaves_：分层树的叶节点数量
  • n_components：连接图中连通分量的估计值
  • children：一个数组，给出了每个非节点数量

方法

  • fit(X[,y])：训练样本
  • fit_predict(X[,y])：训练模型并预测每个样本的簇标记

from sklearn import cluster
from sklearn.metrics import adjusted_rand_score
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs

"""
    产生数据
"""
def create_data(centers,num=100,std=0.7):
    X,labels_true = make_blobs(n_samples=num,centers=centers, cluster_std=std)
    return X,labels_true

"""
    数据作图
"""
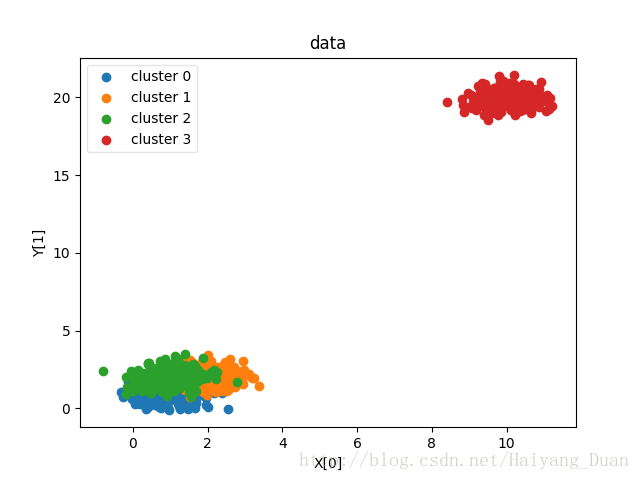
def plot_data(*data):
    X,labels_true=data
    labels=np.unique(labels_true)
    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    colors='rgbycm'
    for i,label in enumerate(labels):
        position=labels_true==label
        ax.scatter(X[position,0],X[position,1],label="cluster %d"%label),
        color=colors[i%len(colors)]

    ax.legend(loc="best",framealpha=0.5)
    ax.set_xlabel("X[0]")
    ax.set_ylabel("Y[1]")
    ax.set_title("data")
    plt.show()
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33

这里写图片描述

这里写代码片
"""
    测试函数
"""  
def test_AgglomerativeClustering(*data):
    X,labels_true=data
    clst=cluster.AgglomerativeClustering()
    predicted_labels=clst.fit_predict(X)
    print("ARI:%s"% adjusted_rand_score(labels_true, predicted_labels))

"""
    考察簇的数量对于聚类效果的影响
"""
def test_AgglomerativeClustering_nclusters(*data):
    X,labels_true=data
    nums=range(1,50)
    ARIS=[]
    for num in nums:
        clst=cluster.AgglomerativeClustering(n_clusters=num)
        predicted_lables=clst.fit_predict(X)
        ARIS.append(adjusted_rand_score(labels_true, predicted_lables)) 

    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    ax.plot(nums,ARIS,marker="+")
    ax.set_xlabel("n_clusters")
    ax.set_ylabel("ARI")
    fig.suptitle("AgglomerativeClustering")
    plt.show()   

"""
    考察链接方式对聚类结果的影响
"""   
def test_agglomerativeClustering_linkage(*data):
    X,labels_true=data
    nums=range(1,50)
    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    linkages=['ward','complete','average']
    markers="+o*"
    for i,linkage in enumerate(linkages): 
        ARIs=[]
        for num in nums:
            clst=cluster.AgglomerativeClustering(n_clusters=num,linkage=linkage)
            predicted_labels=clst.fit_predict(X)
            ARIs.append(adjusted_rand_score(labels_true, predicted_labels))
        ax.plot(nums,ARIs,marker=markers[i],label="linkage:%s"%linkage)

    ax.set_xlabel("n_clusters")
    ax.set_ylabel("ARI")
    ax.legend(loc="best")
    fig.suptitle("AgglomerativeClustering")
    plt.show()
centers=[[1,1],[2,2],[1,2],[10,20]]
X,labels_true=create_data(centers, 1000, 0.5)
test_AgglomerativeClustering(X,labels_true)
plot_data(X,labels_true)
test_AgglomerativeClustering_nclusters(X,labels_true)
test_agglomerativeClustering_linkage(X,labels_true)
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59

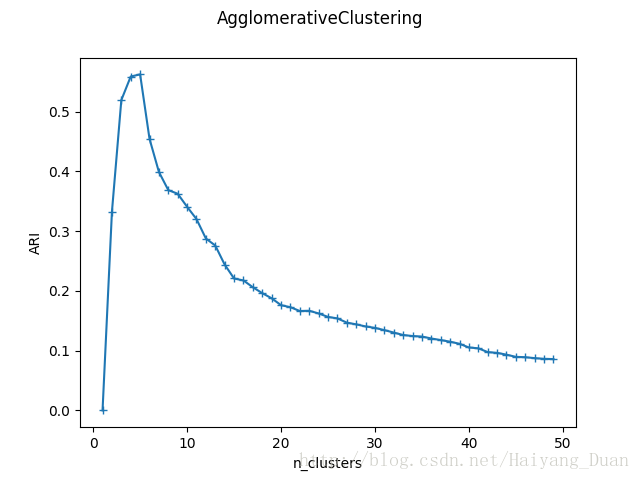
这里写图片描述

可以看到当n_clusters=4时，ARI指数最大，因为确实是从四个中心点产生的四个簇。
  • 1
  • 2

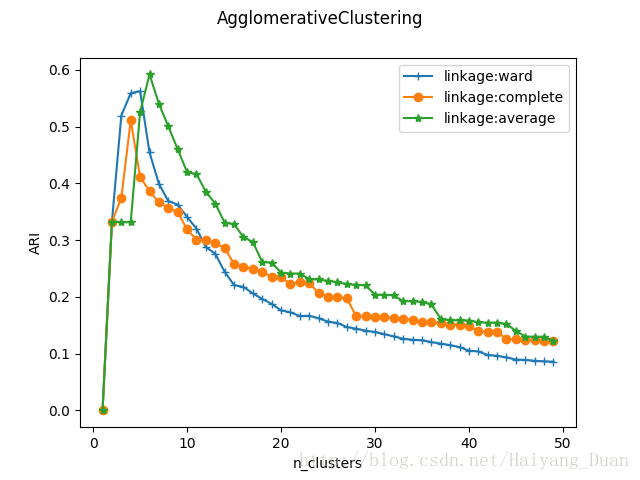
这里写图片描述

 可以看到，三种链接方式随分类簇的数量的总体趋势相差无几。但是单链接方式ward的峰值最大
posted @ 2018-07-01 20:55  交流_QQ_2240410488  阅读(14770)  评论(0)    收藏  举报