最优化方法系列：Adam+SGD-AMSGrad 重点

https://blog.csdn.net/wishchin/article/details/80567558

 

        自动调参的Adam方法已经非常给力了，不过这主要流行于工程界，在大多数科学实验室中，模型调参依然使用了传统的SGD方法，在SGD基础上增加各类学习率的主动控制，以达到对复杂模型的精细调参，以达到刷出最高的分数。

         ICLR会议的 On the convergence of Adam and Beyond 论文，对Adam算法进行了 猛烈的抨击，并提出了新的Adam算法变体。

         以前的文章：最优化方法之GD、SGD ；最优化之回归/拟合方法总结；最优化方法之SGD、Adams；

         参考文章：GD优化算法总结--，可见每一步公式的更新都来之不易。

         优化方法总结：  SGD，Momentum，AdaGrad，RMSProp，Adam.这一篇文章描述简介.

       整个优化系列文章列表：Deep Learning 之 最优化方法；Deep Learning 最优化方法之SGD；Deep Learning 最优化方法之Momentum（动量）；Deep Learning 最优化方法之Nesterov(牛顿动量)；Deep Learning 最优化方法之AdaGrad；Deep Learning 最优化方法之RMSProp；Deep Learning 最优化方法之Adam；

         按章节翻译的中文版-DLBook中文版：https://github.com/exacity/deeplearningbook-chinese

 

Adams算法

      先上结论：

     1.Adam算法可以看做是修正后的Momentum+RMSProp算法

     2.动量直接并入梯度一阶矩估计中（指数加权）

     3.Adam通常被认为对超参数的选择相当鲁棒

     4.学习率建议为0.001

再看算法：其实就是Momentum+RMSProp的结合，然后再修正其偏差。

   

 

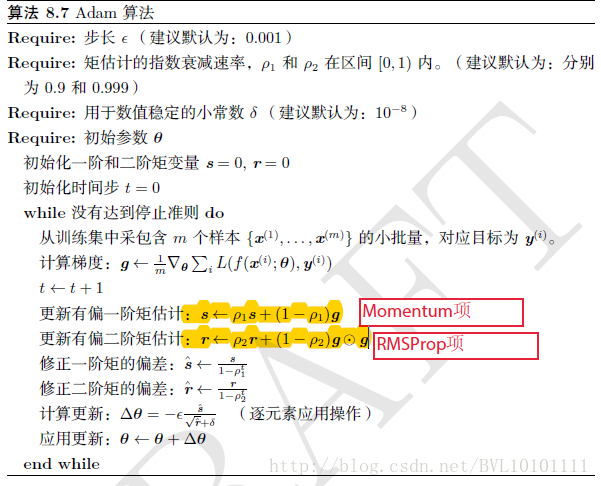
Adams问题

参考：Adams那么棒，为什么对SGD念念不忘-2 ？

1.Adams可能不收敛

文中各大优化算法的学习率：

       

其中，SGD没有用到二阶动量，因此学习率是恒定的（实际使用过程中会采用学习率衰减策略，因此学习率递减）。AdaGrad的二阶动量不断累积，单调递增，因此学习率是单调递减的。因此，这两类算法会使得学习率不断递减，最终收敛到0，模型也得以收敛。

但AdaDelta和Adam则不然。二阶动量是固定时间窗口内的累积，随着时间窗口的变化，遇到的数据可能发生巨变，使得  可能会时大时小，不是单调变化。这就可能在训练后期引起学习率的震荡，导致模型无法收敛。

2.Adams可能错失全局最优解

       吐槽Adam最狠的 The Marginal Value of Adaptive Gradient Methods in Machine Learning 。文中说到，同样的一个优化问题，不同的优化算法可能会找到不同的答案，但自适应学习率的算法往往找到非常差的答案。他们通过一个特定的数据例子说明，自适应学习率算法可能会对前期出现的特征过拟合，后期才出现的特征很难纠正前期的拟合效果。

 

Adams变体方法改进

      会议评论：On the Convergence of Adam and Beyond ； 论文：https://openreview.net/pdf?id=ryQu7f-RZ 。

1. THE NON-CONVERGENCE OF ADAM
      With the problem setup in the previous section, we discuss fundamental flaw in the current exponential moving average methods like ADAM. We show that ADAM can fail to converge to an optimal solution even in simple one-dimensional convex settings. These examples of non-convergence contradict the claim of convergence in (Kingma & Ba, 2015), and the main issue lies in the following quantity of interest:
                                      (2)
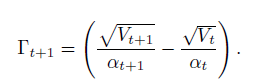
      This quantity essentially measures the change in the inverse of learning rate of the adaptive method with respect to time. One key observation is that for SGD and ADAGRAD, -t 0 for all t 2 [T]. This simply follows from update rules of SGD and ADAGRAD in the previous section. Inparticular, update rules for these algorithms lead to “non-increasing” learning rates. However, this is not necessarily the case for exponential moving average variants like ADAM and RMSPROP i.e., -t can potentially be indefinite for t 2 [T] . We show that this violation of positive definiteness can  lead to undesirable convergence behavior for ADAM and RMSPROP. Consider the following simple sequence of linear functions for F = [-1，1]:
                  
     where C > 2. For this function sequence, it is easy to see that the point x = -1 provides the minimum regret. Suppose 1 = 0 and 2 = 1=(1 + C2). We show that ADAM converges to a highly suboptimal solution of x = +1 for this setting. Intuitively, the reasoning is as follows. The algorithm obtains the large gradient C once every 3 steps, and while the other 2 steps it observes the gradient -1, which moves the algorithm in the wrong direction. The large gradient C is unable to counteract this effect since it is scaled down by a factor of almost C for the given value of 2, and hence the algorithm converges to 1 rather than -1. We formalize this intuition in the result below.
Theorem 1. There is an online convex optimization problem where ADAM has non-zero average regret i.e., RT =T 9 0 as T ! 1.
 We relegate all proofs to the appendix.

       使用指数移动平均值的RMSProp公式有缺陷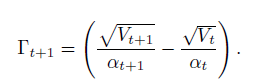，，基本表现了“自适应学习率”优化算法的学习率的倒数相对于时间的变化。 对于SGD和ADAGRAD而言，当t ∈ [T]时，Γt始终大于等于0。这是它们的基本梯度更新规则，所以它们的学习率始终是单调递减的。但是基于指数移动平均值的RMSProp和Adam却没法保证这一点，当t ∈ [T]时，它们的Γt可能大于等于0，也可能小于0。这种现象会导致学习率反复震荡，继而使模型无法收敛。

         以F = [−1, 1]的简单分段线性函数为例：  。当C > 2，在这个函数中，我们很轻松就能看出它应收敛于x = −1。但如果用Adam，它的二阶动量超参数分别是β1 = 0，β2 = 1/(1 + C2)，算法会收敛在x = +1这个点。我们直观推理下：该算法每3步计算一次梯度和，如果其中两步得出的结论是x = -1，而一次得出的结论是C，那么计算指数移动平均值后，算法就会偏离正确收敛方向。因为对于给定的超参数β2，大梯度C没法控制自己带来的不良影响。

 

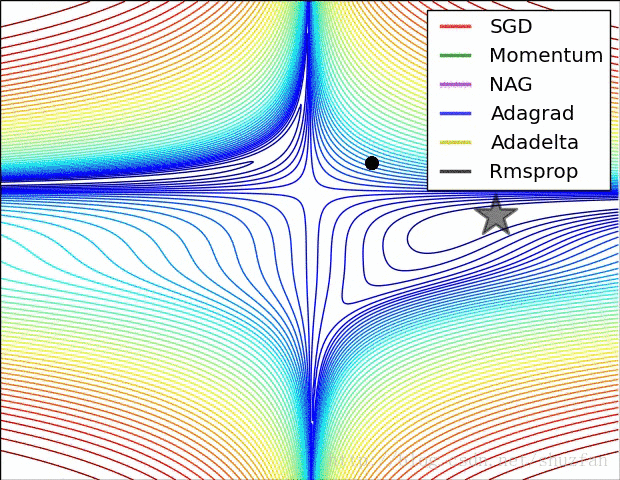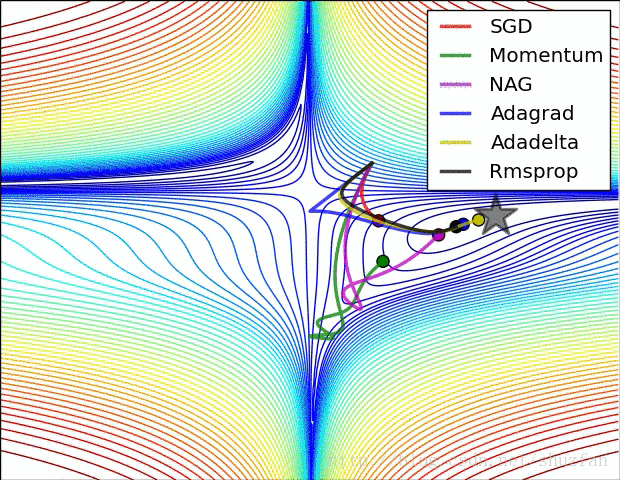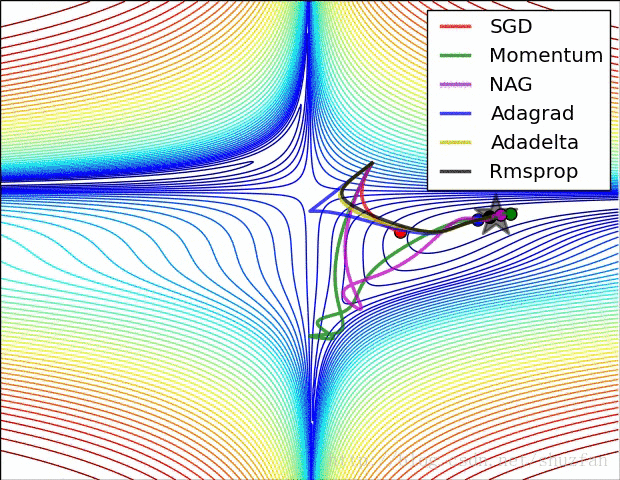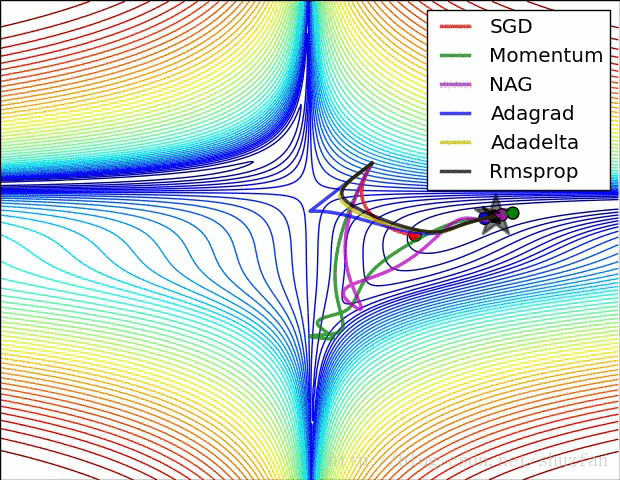
2.来看一个各个优化算法在最优解和鞍点附近的迭代求解图。

  

                                             图片来源：http://imgur.com/a/Hqolp

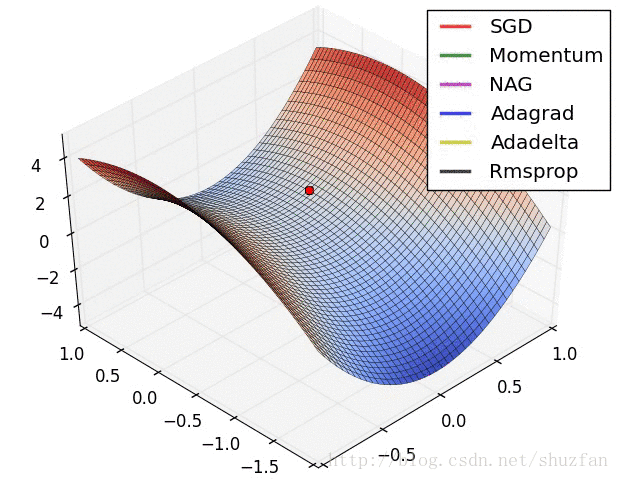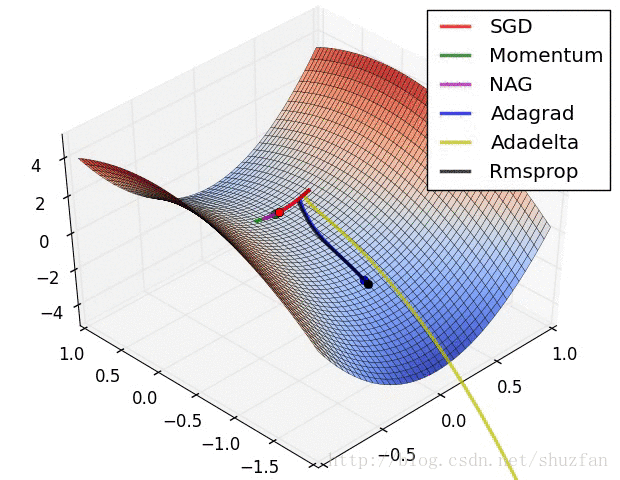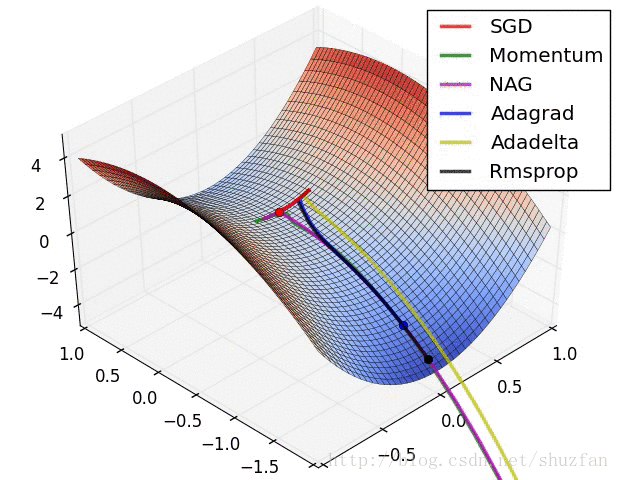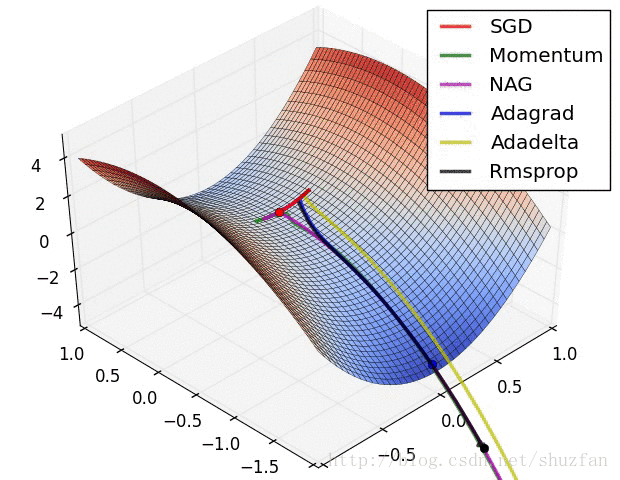
从上图来看，似乎SGD是一种 “最蠢”的方法，不过文献《The Marginal Value of Adaptive Gradient Methods in Machine Learning》给出的结论却是：

       自适应优化算法训练出来的结果通常都不如SGD，尽管这些自适应优化算法在训练时表现的看起来更好。 使用者应当慎重使用自适应优化算法。自适应算法类似于过学习的效果，生成的模型面对整体分布时是过拟合的。

       作者这样阐述：our experimental evidence demonstrates that adaptive methods are not advantageous for machine learning, the Adam algorithm remains incredibly popular. We are not sure exactly as to why, but hope that our step-size tuning suggestions make it easier for practitioners to use standard stochastic gradient methods in their research.这一点貌似不是主要的Adam的缺点。

 

Adams变体AMSGrad

        RMSProp和Adam算法下的Γt可能是负的，所以文章探讨了一种替代方法，通过把超参数β1、β2设置为随着t变化而变化，从而保证Γt始终是个非负数。

      For the first part, we modify these algorithms to satisfy this additional constraint. Later on, we also explore an alternative approach where -t can be made positive semi-definite by using values of 1 and 2 that change with t.     

        

         AMSGRAD uses a smaller learning rate in comparison to ADAM and yet incorporates the intuition of slowly decaying the effect of past gradients on the learning rate as long as -t is positive semidefinite.

         通过添加额外的约束，使学习率始终为正值，当然代价是在大多数时候，AMSGrad算法的学习率是小于Adams和Rmsprop的。它们的主要区别在于AMSGrad记录的是迄今为止所有梯度值vt中的最大值，并用它来更新学习率，而Adam用的是平均值。因此当t ∈ [T]时，AMSGrad的Γt也能做到始终大于等于0。

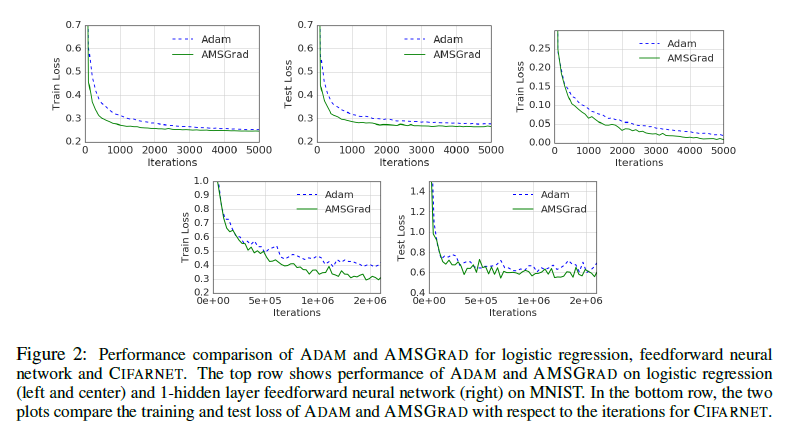
         实验结果

         

 

      

 

多种方法结合

       论文 Improving Generalization Performance by Switching from Adam to SGD，进行了实验验证。他们CIFAR-10数据集上进行测试，Adam的收敛速度比SGD要快，但最终收敛的结果并没有SGD好。他们进一步实验发现，主要是后期Adam的学习率太低，影响了有效的收敛。他们试着对Adam的学习率的下界进行控制，发现效果好了很多。

        于是他们提出了一个用来改进Adam的方法：前期用Adam，享受Adam快速收敛的优势；后期切换到SGD，慢慢寻找最优解。这一方法以前也被研究者们用到，不过主要是根据经验来选择切换的时机和切换后的学习率。这篇文章把这一切换过程傻瓜化，给出了切换SGD的时机选择方法，以及学习率的计算方法，效果看起来也不错。

        时机很重要，把自适应变化为分析数据后，固定优化函数手动切换，理论上能取得更好的效果。又或者，修改Adams算法，以应对Novel情况，保证它的收敛性。