最佳归并树
最佳归并树
归并树的神秘性质
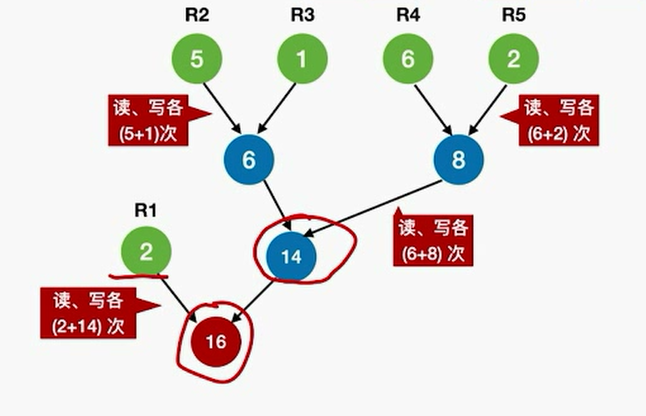
读写磁盘需要2*(6+8+14+16)
每个初始归并段看作一个叶子结点，归并段的长度作为结点权值，则上面这颗归并树的带权路径长度WPL=2 * 1+(5+1+6+2) * 3 = 44 =读磁盘的次数 = 写磁盘的次数
WPL:结点值*到根节点的路径长度
重要结论：归并过程中的磁盘I/O次数 = 归并树的WPL * 2
可以想到：如果要追求归并过程中的磁盘IO次数最小，就要使归并树WPL最小——哈夫曼树
构造2路归并的最佳归并树
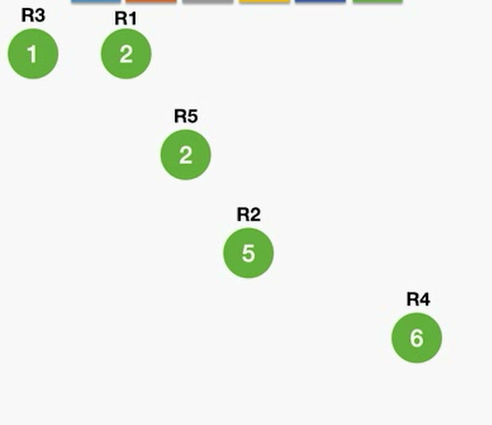
一开始把每一个结点都看成一个个独立的树，接下来在这几颗树中挑选权值最小的两棵树，让他们称为兄弟。新的结点的权值是这两个孩子结点的权值之和。还剩下4颗树
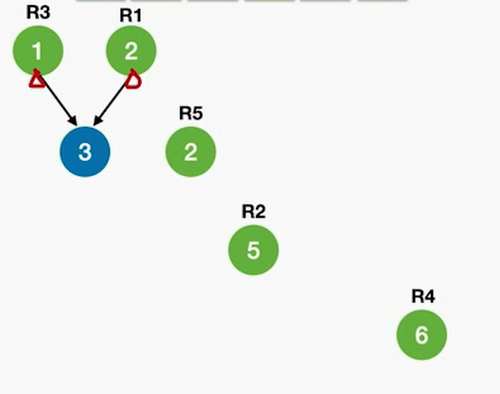
。。。如此操作。。。
\[最佳归并树WPL_{min} = (1+2)*4+2*3+5*2+6*1=34
\]
读磁盘次数 = 写磁盘次数 = 34次
总的磁盘I/O次数 = 68
多路归并的情况
显然不是最佳的归并树
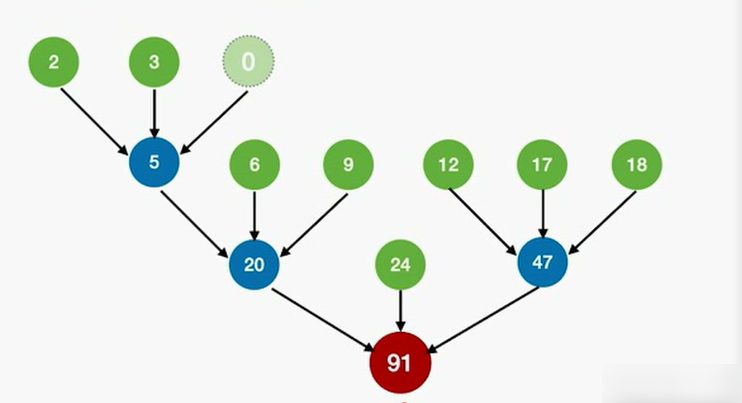
多路归并的最佳归并树
原理和2路归并类似，选择权值最小的3个结点让他们成为兄弟
\[WPL_{min} = (2+3+6)*3 + (9+12+17+24+18)*2 + 30*1 = 223
\]
归并过程中 磁盘的I/O总次数 = 446次
如果减少一个归并段
要做3路归并
不正确！！！！
最后一次归并是2路归并
正确的做法
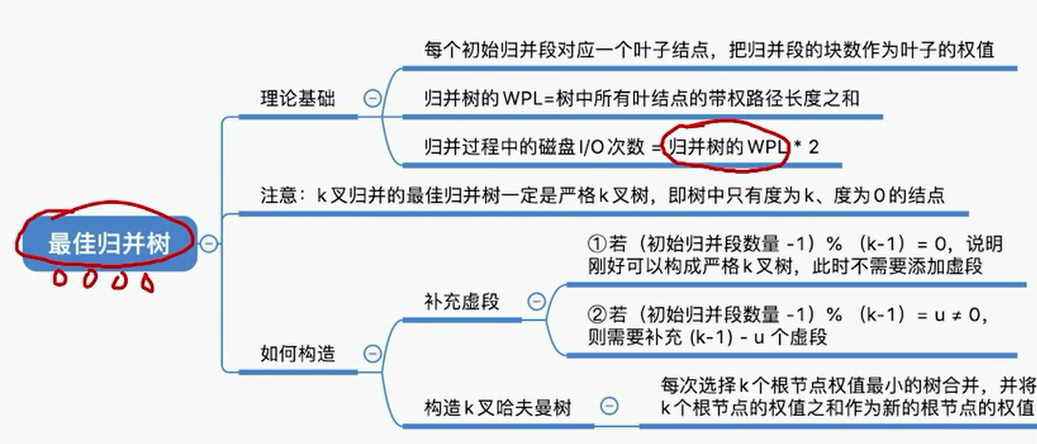
对于k叉归并，若初始归并段的数量无法构成严格的k叉归并树，则需要补充几个长度为0的”虚段“，在进行k叉哈夫曼树的构造。
添加虚段的数量
对于k叉归并，若初始归并段的数量无法构成严格的k叉归并树，则需要补充几个长度为0的”虚段“，在进行k叉哈夫曼树的构造。
k叉的最佳归并树一定是一棵严格的k叉树，即树中只包含度为k、度为0的结点。
知识回顾
