CRF条件随机场基础理解(一)
CRF条件随机场
条件随机场(Conditional Random Fields, 以下简称CRF)是给定一组输入序列条件下另一组输出序列的条件概率分布模型
1.什么样的问题需要CRF模型
(1)我们有一个句子X=“我 是 中国 公民” 需要对这句话中的四个词标注词性,最简单的方法就是拿一组标注好词性的句子作为训练数据,训练逻辑回归分类模型,然后再对句子X中每个词划分类别,但这里面却丢失了一个非常重要的信息,那就是相邻词之间词性存在某种依赖关系,比如名词后面经常接动词、形容词后面经常接名词。CRF可以很好的解决这个问题。
2.马尔科夫随机场到条件随机场
随机场:是由若干个位置组成的整体,当给每一个位置中按照某种分布随机赋予一个值之后,其全体就叫做随机场。还是举词性标注的例子:假如我们有一个四个词形成的句子需要做词性标注。这四个词每个词的词性可以在我们已知的词性集合(名词,动词...)中去选择。当我们为每个词选择完词性后,这就形成了一个随机场。
马尔科夫随机场:马尔科夫随机场是随机场的特例,它假设随机场中某一个位置的赋值仅仅与和它相邻的位置的赋值有关,和与其不相邻的位置的赋值无关。继续举X=“我 是 中国 公民”句子词性标注的例子: 如果我们假设所有词的词性只和它相邻的词的词性有关时,这个随机场就特化成一个马尔科夫随机场。比如第二个词“是”的词性除了与自己本身的位置有关外,只与第一个人称代词“我”和第三个名词“中国”的词性有关。
条件随机场: CRF条件随机场是马尔科夫随机场的特例,它假设马尔科夫随机场中只有X和Y两种变量,X一般是给定的(可以认为是上面举例的四个词的句子),而Y一般是在给定X的条件下我们的输出。这样马尔科夫随机场就特化成了条件随机场。在我们十个词的句子词性标注的例子中,X是词,Y是词性。因此,如果我们假设它是一个马尔科夫随机场,那么它也就是一个CRF。
CRF数学定义:设X与Y是随机变量,P(Y|X)是给定X时Y的条件概率分布,若随机变量Y构成的是一个马尔科夫随机场,则称条件概率分布P(Y|X)是条件随机场。
核心:给定条件X的马尔科夫随机场Y构成一个CRF
3. 从条件随机场到线性链条件随机场
注意在CRF的定义中,我们并没有要求X和Y有相同的结构。而实现中,我们一般都假设X和Y有相同的结构,即:
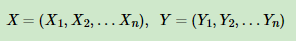
我们一般考虑如下图所示的结构:X和Y有相同的结构的CRF就构成了线性链条件随机场(Linear chain Conditional Random Fields,以下简称 linear-CRF) 在我们的四个词的句子的词性标记中,词有四个,词性也是四个,因此,如果我们假设它是一个马尔科夫随机场,那么它也就是一个linear-CRF。
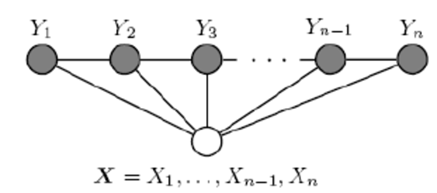
linear-CRF的数学定义:在给定随机变量序列X的情况下,随机变量Y的条件概率分布P(Y|X)构成条件随机场,即满足马尔科夫性:
则称P(Y|X)为线性链条件随机场。
4. 线性链条件随机场的参数化形式
对于上一节讲到的linear-CRF,我们如何将其转化为可以学习的机器学习模型呢?这是通过特征函数和其权重系数来定义的。在linear-CRF中,特征函数分为两类,第一类是定义在Y节点上的节点特征函数,这类特征函数只和当前节点有关,记为:
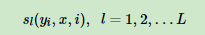
其中L是定义在该节点的节点特征函数的总个数,i是当前节点在序列的位置。
第二类是定义在Y上下文的局部特征函数,这类特征函数只和当前节点和上一个节点有关,记为:

其中K是定义在该节点的局部特征函数的总个数,i是当前节点在序列的位置。之所以只有上下文相关的局部特征函数,没有不相邻节点之间的特征函数,是因为我们的linear-CRF满足马尔科夫性。
无论是节点特征函数还是局部特征函数,它们的取值只能是0或者1。即满足特征条件或者不满足特征条件。同时,我们可以为每个特征函数赋予一个权值,用以表达我们对这个特征函数的信任度。假设tk的权重系数是λk,sl的权重系数是μl,则linear-CRF由我们所有的tk,λk,sl,μl共同决定。此时我们得到了linear-CRF的参数化形式如下:

其中,Z(x)为规范化因子:
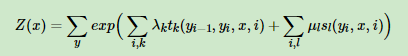
回到特征函数本身,每个特征函数定义了一个linear-CRF的规则,则其系数定义了这个规则的可信度。所有的规则和其可信度一起构成了我们的linear-CRF的最终的条件概率分布。
5. 线性链条件随机场实例
这里我们给出一个linear-CRF用于词性标注的实例,为了方便,我们简化了词性的种类。假设输入的都是三个词的句子,即X=(X1,X2,X3),输出的词性标记为Y=(Y1,Y2,Y3),其中Y∈{1(名词),2(动词)}。这里只标记出取值为1的特征函数如下:
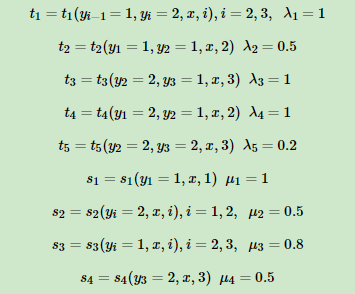
求标记(1,2,2)的非规范化概率。利用linear-CRF的参数化公式,我们有:
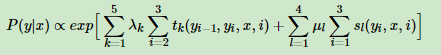
代入值有:
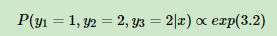
6. 线性链条件随机场的简化形式
在上几节里面,我们用sl表示节点特征函数,用tk表示局部特征函数,同时也用了不同的符号表示权重系数,导致表示起来比较麻烦。其实我们可以对特征函数稍加整理,将其统一起来。
假设我们在某一节点我们有K1个局部特征函数和K2个节点特征函数,总共有K=K1+K2个特征函数。我们用一个特征函数fk(yi−1,yi,x,i)来统一表示如下(分段函数):

7. 线性链条件随机场的矩阵形式
将上一节统一后的linear-CRF公式加以整理,我们还可以将linear-CRF的参数化形式写成矩阵形式。为此我们定义一个m×m的矩阵M,m为y所有可能的状态的取值个数。M定义如下:
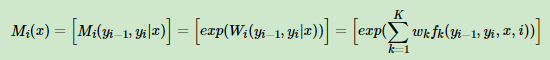
我们引入起点和终点标记y0=start,yn+1=stop, 这样,标记序列y的规范化概率可以通过n+1个矩阵元素的乘积得到,即:
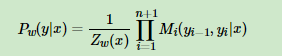
其中Zw(x)为规范化因子



 浙公网安备 33010602011771号
浙公网安备 33010602011771号