[Scikit-learn] 1.9 Naive Bayes

Ref: http://scikit-learn.org/stable/modules/naive_bayes.html

 

1.9.1. Gaussian Naive Bayes

原理可参考：统计学习笔记（4）——朴素贝叶斯法 - 条件概率的应用

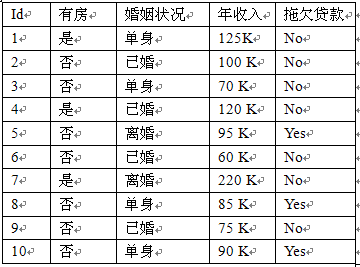
估计示范：X={有房=否，婚姻状况=已婚，年收入=120K}, 假设了 “每个条件都是独立的”。

P(No) * P(有房=否|No) * P(婚姻状况=已婚|No) * P(年收入=120K|No)  = 0.7 * 4/7 * 4/7 * 0.0072 = 0.0024

P(Yes)* P(有房=否|Yes)* P(婚姻状况=已婚|Yes)* P(年收入=120K|Yes) = 0.3 * 1 * 0 * 1.2 * 10^-9 = 0

 

from sklearn import datasets
iris = datasets.load_iris()

from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
y_pred = gnb.fit(iris.data, iris.target).predict(iris.data)
print("Number of mislabeled points out of a total %d points : %d" % (iris.data.shape[0],(iris.target != y_pred).sum()))

Number of mislabeled points out of a total 150 points : 6

可见，有6个比较反常，与“大家”不同。

采用先验分布才是正确的姿势。

 

1.9.2. Multinomial Naive Bayes

import numpy as np
# 0-4之间生成随机数matrix
X = np.random.randint(5, size=(6, 100))
y = np.array([1, 2, 3, 4, 5, 6])　　# X的六行对应六个类别

from sklearn.naive_bayes import MultinomialNB
clf = MultinomialNB()
clf.fit(X, y)print(clf.predict(X[2:3]))　　# 参数必须数组，不能是单个值

 

1.9.3. Bernoulli Naive Bayes

import numpy as np
X = np.random.randint(2, size=(6, 100))
Y = np.array([1, 2, 3, 4, 4, 5])

from sklearn.naive_bayes import BernoulliNB
clf = BernoulliNB()
clf.fit(X, Y)
print(clf.predict(X[2:3]))

  

Others: 

[ML] Naive Bayes for email classification

[ML] Naive Bayes for Text Classification

Goto: [Scikit-learn] 1.1 Generalized Linear Models - Comparing various solvers then classifiers