[Scikit-learn] 1.5 Generalized Linear Models - SGD for Classification
NB: 因为softmax,NN看上去是分类,其实是拟合(回归),拟合最大似然。
多分类参见:[Scikit-learn] 1.1 Generalized Linear Models - Logistic regression & Softmax
感知机采用的是形式最简单的梯度
Perceptron and SGDClassifier share the same underlying implementation.In fact, Perceptron() is equivalent to SGDClassifier(loss=”perceptron”, eta0=1, learning_rate=”constant”, penalty=None).
1.5. Stochastic Gradient Descent
- 1.5.1. Classification
- 1.5.2. Regression
- 1.5.3. Stochastic Gradient Descent for sparse data
- 1.5.4. Complexity
- 1.5.5. Tips on Practical Use
- 1.5.6. Mathematical formulation
- 1.5.7. Implementation details
损失函数
需要一些背景知识,参见斯坦福 CS231n - CNN for Visual Recognition 2 - lecture3
参考:斯坦福CS231n - CNN for Visual Recognition 2 - lecture3 Optimization
一、Loss function 计算
Linear SVM classifier的一个例子。
(1) 计算损失函数:Multiclass SVM loss
一个批次,三张图片,分别得到如下的预测值;而后计算loss。

与"另外两个"的比较:
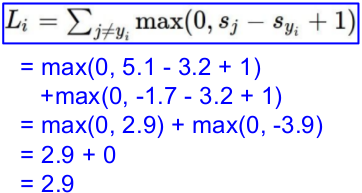
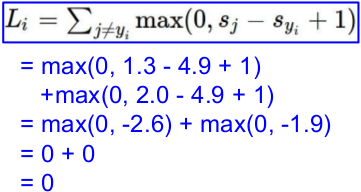
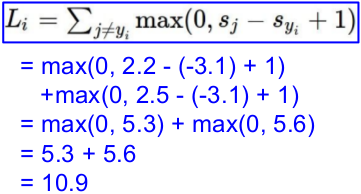
L = (2.9 + 0 + 10.9)/3
= 4.6
(2) 正则化

典型例子说服你:我们当然prefer后一个,w2 。
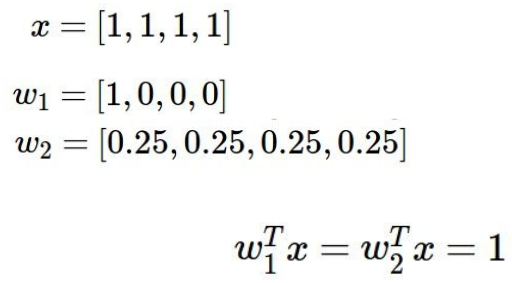
二、其他loss function
Ref: Loss functions for classification

三、loss计算对比
(a) Softmax classifier 的 Softmax's Loss 计算:

(b) Linear SVM classifier 的 hinge loss 计算:
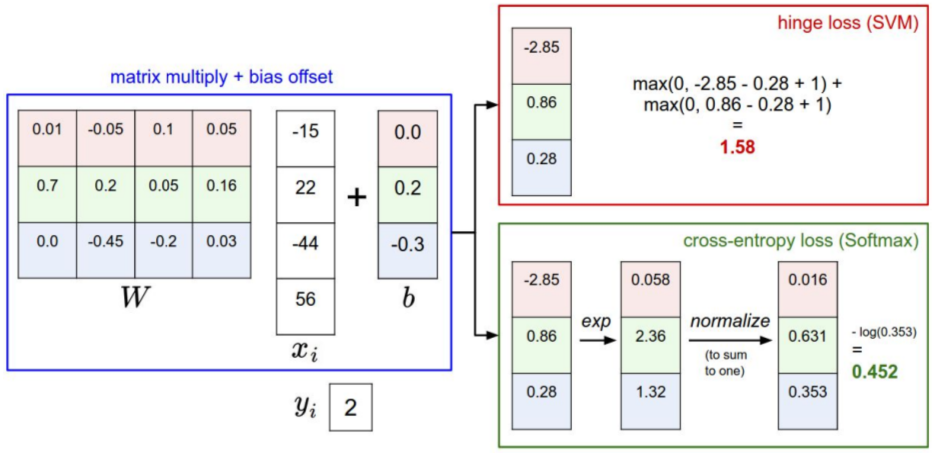

通过该演示体会:http://vision.stanford.edu/teaching/cs231n-demos/linear-classify/
梯度下降
一、逻辑回归
两种损失函数
第一步,逻辑回归的损失函数可以是“得分差”,当然也可以是其他。
第二步,利用“得分差”来进行梯度下降,进行参数优化。
常见有选择两种损失函数,如下:
(1)最小二乘损失函数:逻辑回归与梯度下降法全部详细推导
(2)交叉熵损失函数:机器学习算法 --- 逻辑回归及梯度下降(正统策略)
两个函数接口
Softmax参见:[Scikit-learn] 1.1 Generalized Linear Models - Logistic regression & Softmax
LogisticRegression (交叉熵损失,迭代) versus SGDClassifier(loss="log")
the major difference is the optimization algorithm:
Question: Liblinear/Coordinate Descent vs. Stochastic Gradient Descent.问题:线性梯度下降 vs 随机梯度下降
If your problem is high dimensional (10K or more) and you have a large
number of examples (100K or more) you should choose the latter -
otherwise, LogisticRegression should be fine.高维,更高的数据:随机梯度下降
反之:Liblinear/Coordinate梯度下降
迭代即可,
Both are not proper multinomial logistic regression models;
LogisticRegression does not care and simply computes the probability
estimates of each OVR classifier and normalized to make sure they sum
to one. You could do the same for SGDClassifier(loss='log') but you
have to implement it on your own. You should be aware of the fact that
SGDClassifier(n_jobs > 1) uses multiple processes, thus, if your
dataset (``X``) is too large (more than 50% of your RAM) you'll run
into troubles.
二、梯度下降实践
SGD + Linear SVM classifier
========================================= SGD: Maximum margin separating hyperplane ========================================= Plot the maximum margin separating hyperplane within a two-class separable dataset using a linear Support Vector Machines classifier trained using SGD. """ print(__doc__) import numpy as np import matplotlib.pyplot as plt from sklearn.linear_model import SGDClassifier from sklearn.datasets.samples_generator import make_blobs # we create 50 separable points X, Y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.60)
# 生成样本(上),即刻训练(下)
# fit the model clf = SGDClassifier(loss="hinge", alpha=0.01, n_iter=200, fit_intercept=True) clf.fit(X, Y) # plot the line, the points, and the nearest vectors to the plane xx = np.linspace(-1, 5, 10) yy = np.linspace(-1, 5, 10) X1, X2 = np.meshgrid(xx, yy) Z = np.empty(X1.shape) for (i, j), val in np.ndenumerate(X1): x1 = val x2 = X2[i, j] p = clf.decision_function([[x1, x2]]) Z[i, j] = p[0]
levels = [-1.0, 0.0, 1.0] linestyles = ['dashed', 'solid', 'dashed'] colors = 'k' plt.contour(X1, X2, Z, levels, colors=colors, linestyles=linestyles) plt.scatter(X[:, 0], X[:, 1], c=Y, cmap=plt.cm.Paired) plt.axis('tight') plt.show()
Result:
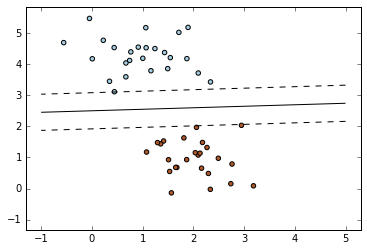
SGDClassifier 的重要参数
具体的损失函数可以通过 loss 参数来设置。SGDClassifier 支持以下几种损失函数:
loss="hinge": (soft-margin) linear Support Vector Machine,loss="modified_huber": smoothed hinge loss,loss="log": logistic regression,- and all regression losses below.
上述中前两个损失函数lazy的,它们只有在某个样本违反了margin(间隔)限制才会更新模型参数,这样的训练过程非常有效,并且可以应用在稀疏模型上,甚至当使用了L2罚项的时候。
具体的罚项可以通过 penalty 参数。SGD支持一下几种罚项:
penalty="l2": L2 norm penalty oncoef_.penalty="l1": L1 norm penalty oncoef_.penalty="elasticnet": Convex combination of L2 and L1;(1 - l1_ratio) * L2 + l1_ratio * L1.
- 默认的设置是
penalty="l2"。L1罚项会导致稀疏的解,使大多数稀疏为0。弹性网络解决了当属性高度相关情况下L1罚项的不足。参数l1_ratio控制 L1 和 L2 罚项的凸组合。
三、多类分类
SGDClassifier 通过组合多个“one versus all(OVA)”形式的二分类器来支持多类分类。
"Softmax 回归 vs. k 个二元分类器 —— 这一选择取决于你的类别之间是否互斥"
对于  类中每个类别,二分类器通过判别该类和其它
类中每个类别,二分类器通过判别该类和其它  类来学习。
类来学习。
通过随机梯度下降解线性分类问题。
"""
========================================
Plot multi-class SGD on the iris dataset
========================================
Plot decision surface of multi-class SGD on iris dataset.
The hyperplanes corresponding to the three one-versus-all (OVA) classifiers
are represented by the dashed lines.
"""
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.linear_model import SGDClassifier
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, :2] # we only take the first two features. We could
# avoid this ugly slicing by using a two-dim dataset
y = iris.target
colors = "bry"
# shuffle 洗牌
idx = np.arange(X.shape[0])
np.random.seed(13)
np.random.shuffle(idx)
X = X[idx]
y = y[idx]
# standardize
mean = X.mean(axis=0)
std = X.std(axis=0)
X = (X - mean) / std
h = .02 # step size in the mesh
clf = SGDClassifier(alpha=0.001, n_iter=100).fit(X, y)
# create a mesh to plot in
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
cs = plt.contourf(xx, yy, Z, cmap=plt.cm.Paired)
plt.axis('tight')
# Plot also the training points
for i, color in zip(clf.classes_, colors):
idx = np.where(y == i)
plt.scatter(X[idx, 0], X[idx, 1], c=color, label=iris.target_names[i],
cmap=plt.cm.Paired)
plt.title("Decision surface of multi-class SGD")
plt.axis('tight')
# Plot the three one-against-all classifiers
xmin, xmax = plt.xlim()
ymin, ymax = plt.ylim()
coef = clf.coef_
intercept = clf.intercept_
def plot_hyperplane(c, color):
def line(x0):
return (-(x0 * coef[c, 0]) - intercept[c]) / coef[c, 1]
plt.plot([xmin, xmax], [line(xmin), line(xmax)],
ls="--", color=color)
for i, color in zip(clf.classes_, colors):
plot_hyperplane(i, color)
plt.legend()
plt.show()
Result:

四、考虑权重的二分类
""" ===================== SGD: Weighted samples ===================== Plot decision function of a weighted dataset, where the size of points is proportional to its weight. """ print(__doc__) import numpy as np import matplotlib.pyplot as plt from sklearn import linear_model # we create 20 points np.random.seed(0) X = np.r_[np.random.randn(10, 2) + [1, 1], np.random.randn(10, 2)] y = [1] * 10 + [-1] * 10 sample_weight = 100 * np.abs(np.random.randn(20)) # and assign a bigger weight to the last 10 samples sample_weight[:10] *= 10 # plot the weighted data points xx, yy = np.meshgrid(np.linspace(-4, 5, 500), np.linspace(-4, 5, 500)) plt.figure() plt.scatter(X[:, 0], X[:, 1], c=y, s=sample_weight, alpha=0.9, cmap=plt.cm.bone) #散点图 ## fit the unweighted model clf = linear_model.SGDClassifier(alpha=0.01, n_iter=100) clf.fit(X, y) Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) no_weights = plt.contour(xx, yy, Z, levels=[0], linestyles=['solid']) ## fit the weighted model clf = linear_model.SGDClassifier(alpha=0.01, n_iter=100) clf.fit(X, y, sample_weight=sample_weight) Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) samples_weights = plt.contour(xx, yy, Z, levels=[0], linestyles=['dashed']) plt.legend([no_weights.collections[0], samples_weights.collections[0]], ["no weights", "with weights"], loc="lower left") plt.xticks(()) plt.yticks(()) plt.show()
Result:
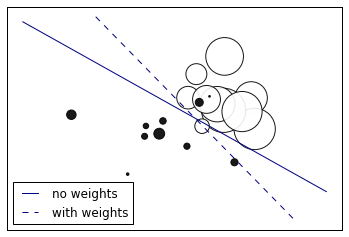
End.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号