[Scikit-learn] 1.1 Generalized Linear Models - from Linear Regression to L1&L2
Introduction
一、Scikit-learning 广义线性模型
From: http://sklearn.lzjqsdd.com/modules/linear_model.html#ordinary-least-squares
# 需要明白以下全部内容,花些时间。

只涉及上述常见的、个人相关的算法。
二、方法进化简史
1.1 松弛求解 到 最小二乘
基本上都是解不存在的超定方程组。因此,需要退一步,将参数求解问题,转化为求最小误差问题,求出一个最接近的解,这就是一个松弛求解。
在回归问题中,线性最小二乘是最普遍的求最小误差的形式。它的损失函数就是二乘损失。如下公式**(1)**所示:
根据使用的正则化类型的不同,回归算法也会有不同。
-
- 普通最小二乘/线性最小二乘回归 不使用 正则化方法。
ridge回归使用L2正则化,lasso回归使用L1正则化。
1.1.1. 普通最小二乘法

证明:https://my.oschina.net/keyven/blog/526010
1.1.2. Ridge
一种专用于共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,
通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法,对病态数据的拟合要强于最小二乘法。
原理:https://wenku.baidu.com/view/52e4e7f7f61fb7360b4c6523.html
岭迹分析:k的选择;变量的选择
1.1.3. Lasso
Lasso 是一种估计稀疏线性模型的方法.由于它倾向具有少量参数值的情况,对于给定解决方案是相关情况下,有效的减少了变量数量。 因此,Lasso及其变种是压缩感知(压缩采样)的基础。
“正则化” 解决 “过拟合”
一、正则化
Ref: 用正则化(Regularization)来解决过拟合
1)控制特征的数目,可以通过特征组合,或者模型选择算法 (参考“岭回归” - 变量的筛选)
2)Regularization,保持所有特征,但是减小每个特征的参数向量θ的大小,使其对分类y所做的共享很小(Ridge and Lasso的特点所在)
p-范数
L0正则化
选择参数非零的特征即可。但因为L0正则化很难求解,是个NP难问题,因此一般采用L1正则化。
L1正则化是L0正则化的最优凸近似,比L0容易求解,并且也可以实现稀疏的效果。
L1正则化
L1正则化在实际中往往替代L0正则化,来防止过拟合。在江湖中也人称Lasso。
L1正则化之所以可以防止过拟合,是因为L1范数就是各个参数的绝对值相加得到的
参数值大小和模型复杂度是成正比的。因此复杂的模型,其L1范数就大,最终导致损失函数就大,说明这个模型就不够好。
L2正则化
L2正则化可以防止过拟合的原因和L1正则化一样,只是形式不太一样。
L2范数是各参数的平方和再求平方根,我们让L2范数的正则项最小,可以使W的每个元素都很小,都接近于0。
但与L1范数不一样的是,它不会使每个元素为0,而只是接近于0。越小的参数说明模型越简单,越简单的模型越不容易产生过拟合现象。
L2正则化江湖人称Ridge,也称“岭回归”
可见,规则化符合奥卡姆剃刀(Occam's razor)原理。
二、几何解释
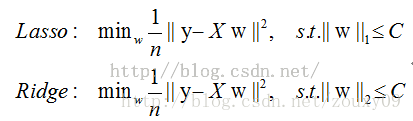
我们考虑两维的情况,在(w1, w2)平面上可以画出目标函数的等高线,而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解:
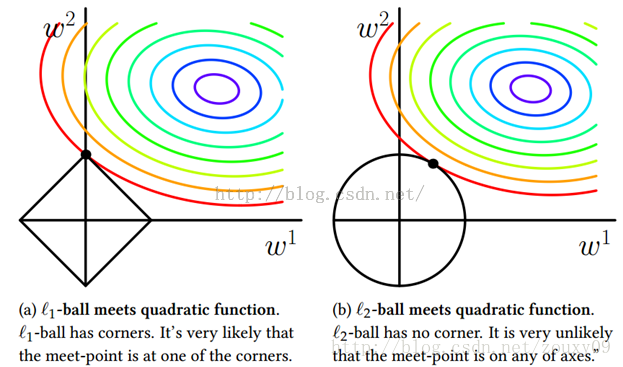
可以看到,L1-ball 与L2-ball 的不同就在于L1在和每个坐标轴相交的地方都有“角”出现,有很大的几率等高线会和L1-ball在四个角,也就是坐标轴上相遇,坐标轴上就可以产生稀疏,因为某一维可以表示为0。而等高线与L2-ball在坐标轴上相遇的概率就比较小了。
总结:L1会趋向于产生少量的特征,而其他的特征都是0,而L2会选择更多的特征,这些特征都会接近于0。Lasso在特征选择时候非常有用,而Ridge就只是一种规则化而已。在所有特征中只有少数特征起重要作用的情况下,选择Lasso比较合适,因为它能自动选择特征。而如果所有特征中,大部分特征都能起作用,而且起的作用很平均,那么使用Ridge也许更合适。
三、发展历史
Ref: 统计学习那些事
Ref: https://cloud.github.com/downloads/cosname/editor/Learning_from_sparsity.pdf
由于篇幅有限,我就以Lasso和Boosting为主线讲讲自己的体会。故事还得从90年代说起。我觉得90年代是这个领域发展的一个黄金年代,因为两种绝世武功都在这个时候横空出世,他们是SVM和Boosted Trees。
SVM
先说SVM。大家对SVM的基本原理普遍表述为,
- SVM通过非线性变换把原空间映射到高维空间,
- 然后在这个高维空间构造线性分类器,因为在高维空间数据点更容易分开。
甚至有部分学者认为SVM可以克服维数灾难(curse of dimensionality)。如果这样理解SVM的基本原理,我觉得还没有看到问题的本质。
因为这个看法不能解释下面的事实:
SVM在高维空间里构建分类器后,为什么这个分类器不会对原空间的数据集Overfitting呢?
要理解SVM的成功,我觉得可以考虑以下几个方面:
-
- 第一,SVM求解最优分类器的时候,使用了L2-norm regularization,这个是控制Overfitting的关键。
- 第二,SVM不需要显式地构建非线性映射,而是通过Kernel trick完成,这样大大提高运算效率。
- 第三,SVM的优化问题属于一个二次规划(Quadratic programming),优化专家们为SVM这个特殊的优化问题设计了很多巧妙的解法,比如SMO(Sequential minimal optimization)解法。
- 第四,Vapnika的统计学习理论为SVM提供了很好的理论背景(这点不能用来解释为什么SVM这么popular,因为由理论导出的bound太loose)。于是SVM成功了,火得一塌糊涂!
Boosted Trees
再说Boosted Trees。它基本的想法是通过对弱分类器的组合来构造一个强分类器。
所谓“弱”就是比随机猜要好一点点;“强”就是强啦。这个想法可以追溯到由Leslie Valiant教授(2010年图灵奖得主)在80年代提出的probably approximately correct learning (PAC learning) 理论。不过很长一段时间都没有一个切实可行的办法来实现这个理想。细节决定成败,再好的理论也需要有效的算法来执行。终于功夫不负有心人, Schapire在1996年提出一个有效的算法真正实现了这个夙愿,它的名字叫AdaBoost。
AdaBoost把多个不同的决策树用一种非随机的方式组合起来,表现出惊人的性能!
-
- 第一,把决策树的准确率大大提高,可以与SVM媲美。
- 第二,速度快,且基本不用调参数。
- 第三,几乎不Overfitting。
我估计当时Breiman和Friedman肯定高兴坏了,因为眼看着他们提出的CART正在被SVM比下去的时候,AdaBoost让决策树起死回生!Breiman情不自禁地在他的论文里赞扬AdaBoost是最好的现货方法(off-the-shelf,即“拿下了就可以用”的意思)。


Breiman and Friedman
其实在90年代末的时候,大家对AdaBoost为什么有如此神奇的性能迷惑不解。
1999年,Friedman的一篇技术报告 “Additive logistic regression: a statistical view of boosting” 解释了大部分的疑惑(没有解释AdaBoost为什么不容易Overfitting,这个问题好像至今还没有定论),即搞清楚了AdaBoost在优化什么指标以及如何优化的。
基于此,Friedman提出了他的GBM(Gradient Boosting Machine,也叫MART或者TreeNet)。几乎在同时,Breiman另辟蹊径,结合他的Bagging (Bootstrap aggregating) 提出了Random Forest (今天微软的Kinect里面就采用了Random Forest,相关论文Real-time Human Pose Recognition in Parts from Single Depth Images是CVPR2011的best paper)。
有一个关于Gradient Boosting细节不得不提。Friedman在做实验的时候发现:
把一棵新生成的决策树,记为f_m,加到当前模型之前,在这棵决策树前乘以一个小的数,即v×f_m(比如v=0.01),再加入到当前模型中,往往大大提高模型的准确度。他把这个叫做“Shrinkage”。(与Lasso的关系)
接下来,Hastie,Tibshirani和Friedman进一步发现(我发现大师们都是亲自动手写程序做实验的),如果把具有Shrinkage的Gradient Boosting应用到线性回归中时,得到的Solution Path与Lasso的Solution Path惊人地相似(如图所示)!他们把这一结果写在了ESL的第一版里,并推测这二者存在着某种紧密的联系,但精确的数学关系他们当时也不清楚。Tibshirani说他们还请教了斯坦福的优化大师(我估计是Stephen Boyd,凸优化的作者),但还是没有找到答案。

后来Tibshirani找到自己的恩师Efron。Tibshirani在“The Science of Bradley Efron”这本书的序言里写道,“He sat down and pretty much single-handedly solved the problem. Along the way, he developed a new algorithm, ‘least angle regression,’ which is interesting in its own right, and sheds great statistical insight on the Lasso.”我就不逐字逐句翻译了,大意是:Efron独自摆平了这个问题,与此同时发明了“Least angle regression (LAR)”。


Efron and Tibshirani
Efron结论是:Lasso和Boosting的确有很紧密的数学联系,它们都可以通过修改LAR得到。更令人惊叹的是LAR具有非常明确的几何意义。于是,Tibshirani在序言中还有一句,“In this work, Brad shows his great mathematical power–not the twentieth century, abstract kind of math, but the old-fashioned kind: geometric insight and analysis.”读Prof Efron的文章,可以感受到古典几何学与现代统计学的结合之美(推荐大家读读Efron教授2010年的一本新书Large-Scale Inference,希望以后有机会再写写这方面的体会)!总之,Efron的这篇文章是现代统计学的里程碑,它结束了一个时代,开启了另一个时代。
这里,想补充说明一下Lasso的身世,它的全称是The Least Absolute Shrinkage and Selection Operator,读音不是[‘læso]而是[læ’su:],有中文翻译为“套索”,个人觉得这个翻译不好,太远离它本来的含义,不如就用Lasso。Tibshrani自己说他的Lasso是受到Breiman的Non-Negative Garrote(NNG)的启发。 Lasso把NNG的两步合并为一步,即L1-norm regularization。Lasso的巨大优势在于它所构造的模型是Sparse的,因为它会自动地选择很少一部分变量构造模型。现在,Lasso已经家喻户晓了,但是Lasso出生后的头两年却很少有人问津。后来Tibshirani自己回忆时说,可能是由下面几个原因造成的:
1. 速度问题:当时计算机求解Lasso的速度太慢;
2. 理解问题:大家对Lasso模型的性质理解不够(直到Efron的LAR出来后大家才搞明白);
3. 需求问题:当时还没有遇到太多高维数据分析的问题,对Sparsity的需求似乎不足。
Lasso的遭遇似乎在阐释我们已经熟知的一些道理:
1.千里马常有,而伯乐不常有(没有Efron的LAR,Lasso可能很难有这么大的影响力)。
2.时势造英雄(高维数据分析的问题越来越多,比如Bioinformatics领域)。
3.金子总是会闪光的。
LAR把Lasso (L1-norm regularization)和Boosting真正的联系起来,如同打通了任督二脉(数学细节可以参考本人的一个小结,当然最好还是亲自拜读Efron的原著)。LAR结束了一个晦涩的时代:
在LAR之前,有关Sparsity的模型几乎都是一个黑箱,它们的数学性质(更不要谈古典的几何性质了)几乎都是缺失。
LAR开启了一个光明的时代:有关Sparsity的好文章如雨后春笋般地涌现,比如Candes和Tao的 Dantzig Selector。伯克利大学的Bin Yu教授称“Lasso, Boosting and Dantzig are three cousins”。近年来兴起的 Compressed sensing 压缩感知(Candes & Tao, Donoho)也与LAR一脉相承,只是更加强调L1-norm regularization其他方面的数学性质,比如Exact Recovery。我觉得这是一个问题的多个方面,
-
- Lasso关注的是构建模型的准确性,
- Compressed sensing关注的是变量选择的准确性。
由此引起的关于Sparsity的研究,犹如黄河泛滥,一发不可收拾。比如Low-rank 逼近是把L1-norm从向量到矩阵的自然推广(现在流行的“用户推荐系统”用到的Collaborative filtering 协同过滤 的数学原理源于此)。有兴趣的童鞋可以参考我个人的小结。
还必须提到的是算法问题。我个人觉得,一个好的模型,如果没有一个快速准确的算法作为支撑的话,它最后可能什么也不是。看看Lasso头几年的冷遇就知道了。LAR的成功除了它漂亮的几何性质之外,还有它的快速算法。
-
- LAR的算法复杂度相当于最小二乘法的复杂度,这几乎已经把Lasso问题的求解推向极致。
这一记录在2007年被Friedman的 Coordinate Descent(CD)坐标下降法 刷新,至今没人打破。Hastie教授趣称这个为“FFT(Friedman + Fortran + Tricks)”。因为CD对Generalized Lasso问题并不能一网打尽,许多凸优化解法应运而生,如Gradient Projection, Proximal methods,ADMM (Alternating Direction Method of Multipliers), (Split) Bregman methods,Nesterov’s method (一阶梯度法中最优的收敛速度,Candes 的很多软件包都根据这个方法设计) 等等。哪个方法更好呢?这个就像问“谁的武功天下第一”一样。我只能回答“王重阳以后再也没有天下第一了,东邪西毒南帝北丐,他们各有各的所长,有的功夫是这个人擅长一些,而另外几门功夫又是另一个人更擅长一些”。有关L1的算法可能还会大量涌现,正如优化大师Stephen Boyd所说(2010年9月28日):“God knows the last thing we need is another algorithm for the Lasso.”
附录:

(Jeff: 以上涉及的常用模型/算法要搞明白,当然最好的笔记总需写在纸上)
代码示范
一、普通最小二乘法
- 统计数据的"获取"和"处理":
#!/usr/bin/python # -*- coding: utf-8 -*- """ ========================================================= Linear Regression Example ========================================================= This example uses the only the first feature of the `diabetes` dataset, in order to illustrate a two-dimensional plot of this regression technique. The straight line can be seen in the plot, showing how linear regression attempts to draw a straight line that will best minimize the residual sum of squares between the observed responses in the dataset, and the responses predicted by the linear approximation. The coefficients, the residual sum of squares and the variance score are also calculated. """ print(__doc__) # 打印上述自我介绍 # Code source: Jaques Grobler # License: BSD 3 clause import matplotlib.pyplot as plt import numpy as np from sklearn import datasets, linear_model # Load the diabetes dataset diabetes = datasets.load_diabetes() # 加载内置数据,matrix # Use only one feature diabetes_X = diabetes.data[:, np.newaxis, 2] # --> # Split the data into training/testing sets diabetes_X_train = diabetes_X[:-20] diabetes_X_test = diabetes_X[-20:] # Split the targets into training/testing sets diabetes_y_train = diabetes.target[:-20] diabetes_y_test = diabetes.target[-20:]
可见,newaxis将数据提高了维度:原来的单个元素,独立成了一维的数据。
diabetes = datasets.load_diabetes()
diabetes
Out[152]:
{'data': array([[ 0.03807591, 0.05068012, 0.06169621, ..., -0.00259226,
0.01990842, -0.01764613],
[-0.00188202, -0.04464164, -0.05147406, ..., -0.03949338,
-0.06832974, -0.09220405],
[ 0.08529891, 0.05068012, 0.04445121, ..., -0.00259226,
0.00286377, -0.02593034],
...,
[ 0.04170844, 0.05068012, -0.01590626, ..., -0.01107952,
-0.04687948, 0.01549073],
[-0.04547248, -0.04464164, 0.03906215, ..., 0.02655962,
0.04452837, -0.02593034],
[-0.04547248, -0.04464164, -0.0730303 , ..., -0.03949338,
-0.00421986, 0.00306441]]),
'target': array([ 151., 75., 141., ..., 132., 220., 57.])}
diabetes_X = diabetes.data[:, np.newaxis, 1]
diabetes_X
Out[156]:
array([[ 0.05068012],
[-0.04464164],
[ 0.05068012],
...,
[ 0.05068012],
[-0.04464164],
[-0.04464164]])
技巧:Cross-validation分割数据集
hao = [1, 2, 3, 4, 5]
hao[:2]
Out[166]: [1, 2]
hao[:-2]
Out[167]: [1, 2, 3]
hao[:-3]
Out[168]: [1, 2]
hao[-3:] # 保证了test set有三个数据
Out[169]: [3, 4, 5]
- 参数训练:
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)
# The coefficients
print('Coefficients: \n', regr.coef_)
# The mean square error
print("Residual sum of squares: %.2f"
% np.mean((regr.predict(diabetes_X_test) - diabetes_y_test) ** 2))
# Explained variance score: 1 is perfect prediction
print('Variance score: %.2f' % regr.score(diabetes_X_test, diabetes_y_test))
- 数据的表达:
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test, color='black')
plt.plot(diabetes_X_test, regr.predict(diabetes_X_test), color='blue', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
二、Ridge regression
"""
===========================================================
Plot Ridge coefficients as a function of the regularization
===========================================================
Shows the effect of collinearity in the coefficients of an estimator.
.. currentmodule:: sklearn.linear_model
:class:`Ridge` Regression is the estimator used in this example.
Each color represents a different feature of the
coefficient vector, and this is displayed as a function of the
regularization parameter.
At the end of the path, as alpha tends toward zero
and the solution tends towards the ordinary least squares, coefficients
exhibit big oscillations.
"""
# Author: Fabian Pedregosa -- <fabian.pedregosa@inria.fr>
# License: BSD 3 clause
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# X is the 10x10 Hilbert matrix
X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)
###############################################################################
# Compute paths
n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas) # 非常好的体现变化细节的技巧
clf = linear_model.Ridge(fit_intercept=False)
coefs = []
for a in alphas:
clf.set_params(alpha=a)
clf.fit(X, y)
coefs.append(clf.coef_) # 不是一个参数,而是持续得到一组参数
###############################################################################
# Display results
ax = plt.gca()
ax.set_color_cycle(['b', 'r', 'g', 'c', 'k', 'y', 'm'])
ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')
plt.show()
根据Ridge trace图,开始alpha的选取,以及变量的选取问题。当然,这其中也体现了其仍遗留的缺陷,如下。

三、Lasso regression
鉴于其重要性,另起一章学习 [Scikit-learn] 1.1. Generalized Linear Models - Lasso Regression
Extended: 特征相关性对于DL的影响
Goto [CNN] Feature Selection in training of Deep Learning




 浙公网安备 33010602011771号
浙公网安备 33010602011771号