[TF] Architecture - Computational Graphs

阅读笔记：

仅希望对底层有一定必要的感性认识，包括一些基本核心概念。

Here只关注Graph相关，因为对编程有益。

TF – Kernels模块部分参见：https://mp.weixin.qq.com/s/vwSlxxD5Ov0XwQCKy1oyuQ

TF – Session部分，也可以在起专题总结：https://mp.weixin.qq.com/s/Bi6Rg-fEwyN4uIyRHDPhXg

Tensorflow Download: https://github.com/tensorflow/tensorflow/releases

From: https://zhuanlan.zhihu.com/p/25646408

-- 大纲 --

本文依据对Tensorflow（简称TF）

- 白皮书[1]、
- TF Github[2]
- TF官方教程[3]的理解，

从系统和代码实现角度讲解TF的内部实现原理。

以Tensorflow r0.8.0为基础，本文由浅入深的阐述Tensor和Flow的概念。

先介绍了TensorFlow的核心概念和基本概述，然后剖析了OpKernels模块、Graph模块、Session模块。

1.2 TF系统架构

若干要点：

第五、六层	应用层	实现相关实验和应用
第四层	API接口层	对TF功能模块的接口封装，便于其他语言平台调用
第三层	图计算层（Graph）	本地计算流图 and 分布式计算流图的实现	包含：Graph的创建、编译、优化和执行等部分，Graph中每个节点都是OpKernels类型表示。
第二层	OpKernels	以Tensor为处理对象，实现了各种Tensor操作或计算	包含：MatMul等计算操作，也包含Queue等非计算操作
第一层	gRPC	网络通信依赖gRPC通信协议实现不同设备间的数据传输和更新

1.3TF代码目录组织

Tensorflow/core目录 - 包含了TF核心模块代码。

public: API接口头文件目录，用于外部接口调用的API定义，主要是session.h 和tensor_c_api.h。

client: API接口实现文件目录。

platform: OS系统相关接口文件，如file system, env等。

protobuf: 均为.proto文件，用于数据传输时的结构序列化.

common_runtime: 公共运行库，包含session, executor, threadpool, rendezvous, memory管理, 设备分配算法等。

distributed_runtime: 分布式执行模块，如rpc session, rpc master, rpc worker, graph manager。

framework: 包含基础功能模块，如log, memory, tensor

graph: 计算流图相关操作，如construct, partition, optimize, execute等

kernels: 核心Op，如matmul, conv2d, argmax, batch_norm等

lib: 公共基础库，如gif、gtl(google模板库)、hash、histogram等。

ops: 基本ops运算，ops梯度运算，io相关的ops，控制流和数据流操作

Tensorflow/stream_executor目录 - 并行计算框架，由google stream executor团队开发。

Tensorflow/contrib目录 - contributor开发目录。

Tensroflow/python目录 - python API客户端脚本。

Tensorflow/tensorboard目录 - 可视化分析工具，不仅可以模型可视化，还可以监控模型参数变化。

third_party目录 - TF第三方依赖库。

eigen3: eigen矩阵运算库，TF基础ops调用

gpus: 封装了cuda/cudnn编程库

2. TF核心概念

TF的核心是围绕Graph展开的，

简而言之，就是Tensor 完成Flow的过程。

所以，在介绍Graph之前需要讲述一下 (1) 符号编程、(2) 计算流图、(3) 梯度计算、(4) 控制流的概念。

2.1 Tensor

在数学上，Matrix表示二维线性映射，Tensor表示多维线性映射，Tensor是对Matrix的泛化，可以表示1-dim、2-dim、N-dim的高维空间。

图 2 1对比了矩阵乘法（Matrix Product）和张量积（Tensor Contract），可以看出Tensor的泛化能力，其中张量积运算在TF的MatMul和Conv2D运算中都有用到，

Tensor在高维空间数学运算比Matrix计算复杂，计算量也非常大，加速张量并行运算是TF优先考虑的问题，如add, contract, slice, reshape, reduce, shuffle等运算。

TF中Tensor的维数描述为阶，数值是0阶，向量是1阶，矩阵是2阶，以此类推，可以表示n阶高维数据。

TF中Tensor支持的数据类型有很多，如tf.float16, tf.float32, tf.float64, tf.uint8, tf.int8, tf.int16, tf.int32, tf.int64, tf.string, tf.bool, tf.complex64等，所有Tensor运算都使用泛化的数据类型表示。

TF的Tensor定义和运算主要是调用 Eigen矩阵计算库完成的。

【Eigen矩阵运算库】

Eigen is a C++ template library for linear algebra: matrices, vectors, numerical solvers, and related algorithms.

Download: http://eigen.tuxfamily.org/index.php?title=Main_Page

简单说一下Eigen的特点：

(1) 使用方便、无需预编译，调用开销小

(2) 函数丰富，风格有点近似MATLAB，易上手；

(3) 速度中规中矩，比OpenCV快，比MKL、openBLAS慢；

TF中Tensor的UML定义如图 2 2。其中TensorBuffer指针指向Eigen::Tensor类型。其中，Eigen::Tensor[5][6]不属于Eigen官方维护的程序，由贡献者提供文档和维护，所以Tensor定义在Eigen unsupported模块中。

图 2 2中，Tensor主要包含两个变量m_data和m_dimension，

- m_data保存了Tensor的数据块，T是泛化的数据类型，
- m_dimensions保存了Tensor的维度信息。

Eigen::Tensor的成员变量很简单，却支持非常多的基本运算，再借助Eigen的加速机制实现快速计算，参考章节3.2。

Eigen::Tensor主要包含了

一元运算（Unary），如sqrt、square、exp、abs等。

二元运算（Binary），如add，sub，mul，div等

选择运算（Selection），即if/else条件运算

归纳运算（Reduce），如reduce_sum， reduce_mean等

几何运算（Geometry），如reshape，slice，shuffle，chip，reverse，pad，concatenate，extract_patches，extract_image_patches等

张量积（Contract）和卷积运算（Convolve）是重点运算，后续会详细讲解。

2.2 符号编程

编程模式通常分为命令式编程（imperative style programs）和符号式编程（symbolic style programs）。

- 命令式编程容易理解和调试，命令语句基本没有优化，按原有逻辑执行。 --> Torch是典型的命令式风格
- 符号式编程涉及较多的嵌入和优化，不容易理解和调试，但运行速度有同比提升。 --> theano和Tensorflow都使用了符号式编程。

caffe、mxnet 则采用了两种编程模式混合的方法。

* 命令式编程是常见的编程模式，编程语言如python/C++都采用命令式编程。

* 符号式编程将计算过程抽象为计算图，计算流图可以方便的描述计算过程，所有输入节点、运算节点、输出节点均符号化处理。

计算图通过建立输入节点到输出节点的传递闭包，从输入节点出发，沿着传递闭包完成数值计算和数据流动，until达到输出节点。

这个过程经过计算图优化，以数据（计算）流方式完成，节省内存空间使用，计算速度快，但不适合程序调试，通常不用于编程语言中。

举上面的例子，先根据计算逻辑编写符号式程序并生成计算图

其中A和B是输入符号变量，C和D是运算符号变量，compile函数生成计算图F，如图 2 3所示。

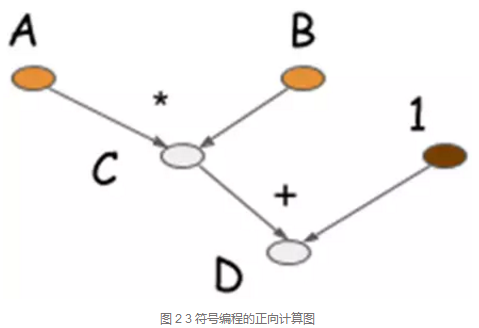
最后得到A=10, B=10时变量D的值，这里D可以复用C的内存空间，省去了中间变量的空间存储。

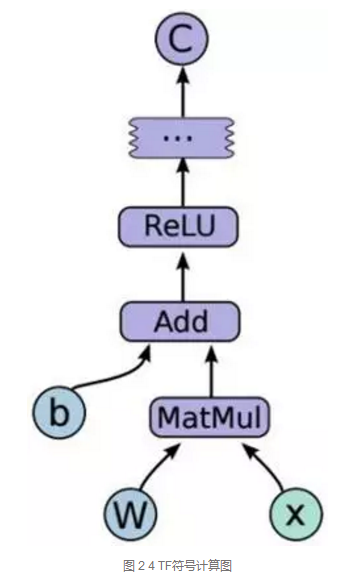
图 2 4是TF中的计算流图，C=F(Relu(Add(MatMul(W, x), b)))，其中每个节点都是符号化表示的。

通过session创建graph，在调用session.run执行计算。

和目前的符号语言比起来，TF最大的特点是强化了数据流图，引入了mutation的概念。这一点是TF和包括Theano在内的符号编程框架最大的不同。

所谓mutation，就是可以在计算的过程更改一个变量的值，而这个变量在计算的过程中会被带入到下一轮迭代里面去。

Mutation是机器学习优化算法几乎必须要引入的东西（虽然也可以通过immutable replacement来代替，但是会有效率的问题）。

Theano的做法是引入了update statement来处理mutation。

小总结

TF选择了纯符号计算的路线，并且直接把更新引入了数据流图中去。(两大特点)

2.3 梯度计算

梯度计算主要应用在误差反向传播和数据更新，是深度学习平台要解决的核心问题。

梯度计算涉及每个计算节点，每个自定义的前向计算图都包含一个隐式的反向计算图。

从数据流向上看，

- 正向计算图：数据从输入节点到输出节点的流向过程，
- 反向计算图：数据从输出节点到输入节点的流向过程。

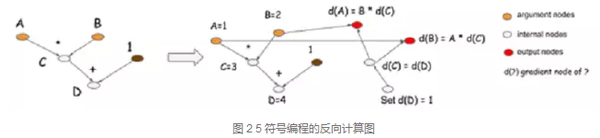
图 2 5是2.2节中图 2 3对应的反向计算图。图中，由于C=A*B，则dA=B*dC, dB=A*dC。

在反向计算图中，输入节点dD，输出节点dA和dB，计算表达式为dA=B*dC=B*dD, dB=A*dC=A*dD。每一个正向计算节点对应一个隐式梯度计算节点。

反向计算限制了符号编程中内存空间复用的优势，因为在正向计算中的计算数据在反向计算中也可能要用到。

从这一点上讲，粗粒度的计算节点比细粒度的计算节点更有优势，而TF大部分为细粒度操作，虽然灵活性很强，但细粒度操作涉及到更多的优化方案，在工程实现上开销较大，不及粗粒度简单直接。在神经网络模型中，TF将逐步侧重粗粒度运算。

2.4 控制流

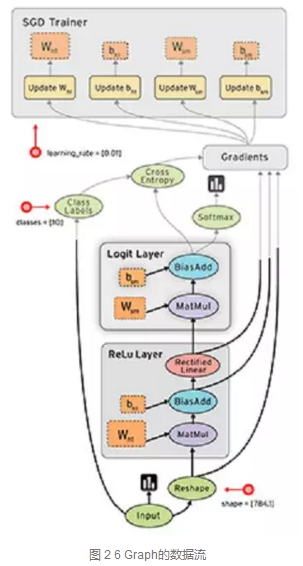
TF的计算图如同数据流一样，数据流向表示计算过程，如图 2 6。数据流图可以很好的表达计算过程，为了扩展TF的表达能力，TF中引入控制流。

// 感受”条件判断“的区别

在编程语言中，if…else…是最常见的逻辑控制，在TF的数据流中也可以通过这种方式控制数据流向。接口函数如下，

- pred为判别表达式，
- fn1和fn2为运算表达式。

当pred为true是，执行fn1操作；当pred为false时，执行fn2操作。

tf.cond(pred, fn1, fn2, name=None)

TF还可以协调多个数据流，在存在依赖节点的场景下非常有用，例如节点B要读取模型参数θ更新后的值，而节点A负责更新参数θ，则节点B必须等节点A完成后才能执行，否则读取的参数θ为更新前的数值，这时需要一个运算控制器。接口函数如下，tf.control_dependencies函数可以控制多个数据流执行完成后才能执行接下来的操作，通常与tf.group函数结合使用。

tf.control_dependencies(control_inputs)

TF支持的控制算子有Switch、Merge、Enter、Leave和NextIteration等。

TF不仅支持逻辑控制，还支持循环控制。TF使用和MIT Token-Tagged machine相似的表示系统，将循环的每次迭代标记为一个tag，迭代的执行状态标记为一个frame，但迭代所需的数据准备好的时候，就可以开始计算，从而多个迭代可以同时执行。

反向计算限制了符号编程中内存空间复用的优势，因为在正向计算中的计算数据在反向计算中也可能要用到。从这一点上讲，粗粒度的计算节点比细粒度的计算节点更有优势，而TF大部分为细粒度操作，虽然灵活性很强，但细粒度操作涉及到更多的优化方案，在工程实现上开销较大，不及粗粒度简单直接。在神经网络模型中，TF将逐步侧重粗粒度运算。

From: https://mp.weixin.qq.com/s/-sYn6j3Xiljzw3T6DoJeCA

3. TF 代码分析初步

3.1 TF总体概述

如图 3 1所示是一个简单线性模型的TF正向计算图和反向计算图。图中

- x是输入，
- W是参数权值，
- b是偏差值，
- MatMul和Add是计算操作，
- dMatMul和dAdd是梯度计算操作，
- C是正向计算的目标函数，
- 1是反向计算的初始值，
- dC/dW和dC/dx是模型参数的梯度函数。

图 3 1 tensorflow计算流图示例

以图 3 1为例实现的TF代码见图 3 2(略)。

- 首先声明参数变量W、b和输入变量x，构建线性模型y=W*x+b，
- 目标函数loss采用误差平方和最小化方法，
- 优化函数optimizer采用随机梯度下降方法。
- 然后初始化全局参数变量，
- 利用session与master交互实现图计算。

图 3 2 TF线性模型示例的实现代码

图 3 2中summary可以记录graph元信息和tensor数据信息，再利用tensorboard分析模型结构和训练参数。

图 3 3是上述代码在Tensorboard中记录下的Tensor跟踪图。Tensorboard可以显示scaler和histogram两种形式。跟踪变量走势可更方便的分析模型和调整参数。

图 3 3 Tensorboard显示的TF线性模型参数跟踪

图 3 4是图 3 1示例在Tensorboard中显示的graph图。

左侧子图描述的正向计算图和反向计算图，正向计算的输出被用于反向计算的输入，其中MatMul对应MatMul_grad，Add对应Add_grad等。

右上侧子图指明了目标函数最小化训练过程中要更新的模型参数W、b，右下侧子图是参数节点W、b展开后的结果。

图 3 4中，参数W是命名空间（Namespace）类型，展开后的W主要由Assign和Read两个OpNode组成，分别负责W的赋值和读取任务。

命名空间gradients是隐含的反向计算图，定义了反向计算的计算逻辑。

从图 3 1可以看出，更新参数W需要先计算dMatMul，即图 3 4中的MatMul_grad操作，而Update_W节点负责更新W操作。

为了进一步了解UpdateW的逻辑，图 3 5对MatMul_grad和update_W进行了展开分析。

图 3 5 MatMul_grad计算逻辑

图 3 5中，

子图(a)描述了MatMul_grad计算逻辑，
子图(b)描述了MatMul_grad输入输出，
子图(c)描述了update_W的计算逻辑。

首先明确MatMul矩阵运算法则，假设 z=MatMul(x, y)，则有dx = MatMul(dz, y)，dy = MatMul(x, dz)，由此可以推出dW=MatMul(dAdd, x)。

在子图(a)中左下侧的节点b就是输入节点x，dAdd由Add_grad计算输出。

update_W的计算逻辑由最优化函数指定，而其中的minimize/update_W/ApplyGradientDescent变量决定，即子图(b)中的输出变量Outputs。

另外，在MatMul_grad/tuple命名空间中还隐式声明了control dependencies控制依赖操作，这在章节2.4控制流中相关说明。

看到这里，对计算流图的理解需要深入一些：http://blog.csdn.net/tinyzhao/article/details/52755647

核心概念的补充：

计算图的若干概念

在TensorFlow中，算法都被表示成计算图（computational graphs）。计算图也叫数据流图，可以把计算图看做是一种有向图，图中的节点表示操作，图中的边代表在不同操作之间的数据流动。

在这样的数据流图中，有四个主要的元素：
* 操作 (operations)
* 张量 (tensors)
* 变量 (variables)
* 会话 (sessions)

操作

把算法表示成一个个操作的叠加，可以非常清晰地看到数据之间的关系，而且这样的基本操作也具有普遍性。

在TensorFlow中，当数据流过操作节点的时候就可以对数据进行操作。一个操作可以有零个或多个输入，产生零个或多个输出。

一个操作可能是一次数学计算，一个变量或常量，一个数据流走向控制，一次文件IO或者是一次网络通信。

其中，一个常量可以看做是没有输入，只有一个固定输出的操作。具体操作如下所示：

操作类型	例子
元素运算	Add,Mul
矩阵运算	MatMul,MatrixInverse
数值产生	Constant,Variable
神经网络单元	SoftMax,ReLU,Conv2D
I/O	Save,Restore

每一种操作都需要相对应的底层计算支持，比如在GPU上使用就需要实现在GPU上的操作符，在CPU上使用就要实现在CPU上的操作符。

张量 (多维的数组或者高维的矩阵，是个引用)

在计算图中，每个边就代表数据从一个操作流到另一个操作。这些数据被表示为张量，一个张量可以看做是多维的数组或者高维的矩阵。
关于TensorFlow中的张量，需要注意的是张量本身并没有保存任何值，张量仅仅提供了访问数值的一个接口，可以看做是数值的一种引用。

在TensorFlow实际使用中我们也可以发现，在run之前的张量并没有分配空间，此时的张量仅仅表示了一种数值的抽象，用来连接不同的节点，表示数据在不同操作之间的流动。
TensorFlow中还提供了SparseTensor数据结构，用来表示稀疏张量。

变量

变量是计算图中可以改变的节点。比如当计算权重的时候，随着迭代的进行，每次权重的值会发生相应的变化，这样的值就可以当做变量。

在实际处理时，一般把需要训练的值指定为变量。在使用变量的时候，需要指定变量的初始值，变量的大小和数据类型就是根据初始值来推断的。

在构建计算图的时候，指定一个变量实际上需要增加三个节点：

* 实际的变量节点
* 一个产生初始值的操作，通常是一个常量节点
* 一个初始化操作，把初始值赋予到变量

初始化一个变量：

如图所示，v代表的是实际的变量，i是产生初始值的节点，上面的assign节点将初始值赋予变量，assign操作以后，产生已经初始化的变量值v'。

会话 ('操作'在其中)

在TensorFlow中，所有操作都必须在会话（session）中执行，会话负责分配和管理各种资源。

在会话中提供了一个run方法，可以用它来执行计算图整体或者其中的一部分节点。

在进行run的时候，还需要用feed_dict把相关数据输入到计算图。

当run被调用的时候，TensorFlow将会从指定的输出节点开始，向前查找所有的依赖界节点，所有依赖节点都将被执行。

这些操作随后将被分配到物理执行单元上（比如CPU或GPU），这种分配规则由TensorFlow中的分配算法决定。

反向传播的计算图

在神经网络训练中，需要使用到反向传播算法。

在TensorFlow等深度学习框架中，梯度计算都是自动进行的，不需要人工进行梯度计算，

- 这样只需要使用者定义网络的结构，
- 其他工作都由深度学习框架自动完成，大大简化了算法验证。

在TensorFlow中，梯度计算也是采用了计算图的结构。

梯度计算

如图，在神经网络中常常需要对权重w进行求导。这样的函数前向计算的式子为:

z=h(y)，y=g(x)，x=f(w)

对应链式求导法则：

整合一下就可以得到：

z=h(g(f(w)))

3.2 Eigen介绍（略）

3.3 设备内存管理（略）

3.4 TF开发工具介绍

TF系统开发使用了：

1. bazel工具实现工程代码自动化管理，
2. protobuf实现了跨设备数据传输，
3. swig库实现python接口封装。

SWIG 是Simple Wrapper and Interface Generator的缩写，是一个帮助使用C或者C++编写的软件创建其他编语言的API的工具。例如，我想要为一个C++编写的程序创建.NET API，一般情况下我必须使用托管C++(Managed C++)去编写大量的代码才能生成它的.NET API。有了SWIG，这个机械的工作将变得非常简单。你只须要使用一个接口文件告诉SWIG要为那些类创建.NET API，SWIG就会自动帮你生成它的.NET API。

 当 然，SWIG不仅仅支持创建.NET API。最新版本的SWIG支持常用脚本语言Perl、PHP、Python、Tcl、Ruby和非脚本语言C#, Common Lisp (CLISP, Allegro CL, CFFI, UFFI), Java, Modula-3, OCAML以及R，甚至是编译器或者汇编的计划应用（Guile, MzScheme, Chicken）。

SWIG简介

以下将从这三方面介绍TF开发工具的使用。

3.4.1 Swig封装

Tensorflow核心框架使用C++编写，API接口文件定义在tensorflow/core/public目录下，主要文件是tensor_c_api.h文件，C++语言直接调用这些头文件即可。

Python通过Swig工具封装TF库包间接调用，接口定义文件tensorflow/python/ tensorflow.i。其中swig全称为Simplified Wrapper and Interface Generator，是封装C/C++并与其它各种高级编程语言进行嵌入联接的开发工具，对swig感兴趣的请参考相关文档。

在tensorflow.i文件中包含了若干个.i文件，每个文件是对应模块的封装，其中tf_session.i文件中包含了tensor_c_api.h，实现client向session发送请求创建和运行graph的功能。

3.4.2 Bazel编译和调试

Bazel是Google开源的自动化构建工具，类似于Make和CMake工具。Bazel的目标是构建“快速并可靠的代码”，并且能“随着公司的成长持续调整其软件开发实践”。

TF中几乎所有代码编译生成都是依赖Bazel完成的，了解Bazel有助于进一步学习TF代码，尤其是编译测试用例进行gdb调试。

Bazel假定每个目录为[package]单元，目录里面包含了源文件和一个描述文件BUILD，描述文件中指定了如何将源文件转换成构建的输出。

以图 3 13为例，左子图为工程中不同模块间的依赖关系，右子图是对应模块依赖关系的BUILD描述文件。

图 3 13中name属性来命名规则，srcs属性为模块相关源文件列表，deps属性来描述规则之间的依赖关系。”//search: google_search_page”中”search”是包名，”google_search_page”为规则名，其中冒号用来分隔包名和规则名；如果某条规则所依赖的规则在其他目录下，就用"//"开头，如果在同一目录下，可以忽略包名而用冒号开头。

图 3 13中cc_binary表示编译目标是生成可执行文件，cc_library表示编译目标是生成库文件。如果要生成google_search_page规则可运行

如果要生成可调试的二进制文件，可运行

图 3 13 Bazel BUILD文件示例

TF中首次运行bazel时会自动下载很多依赖包，如果有的包下载失败，打开tensorflow/workspace.bzl查看是哪个包下载失败，更改对应依赖包的new_http_archive中的url地址，也可以把new_http_archive设置为本地目录new_local_repository。

TF中测试用例跟相应代码文件放在一起，如MatMul操作的core/kernels/matmul_op.cc文件对应的测试用例文件为core/kernels/matmul_op_test.cc文件。

运行这个测试用例需要查找这个测试用例对应的BUILD文件和对应的命令规则，如matmul_op_test.cc文件对应的BUILD文件为core/kernels/BUILD文件，如下

其中tf_cuda_cc_test函数是TF中自定义的编译函数，函数定义在/tensorflow/ tensorflow.bzl文件中，它会把matmul_op_test.cc放进编译文件中。要生成matmul_op_test可执行文件可运行如下脚本：

3.4.3 Protobuf序列化

Protocol Buffers 是一种轻便高效的结构化数据存储格式，可以用于结构化数据串行化，或者说序列化。它很适合做数据存储或 RPC 数据交换格式。可用于通讯协议、数据存储等领域的语言无关、平台无关、可扩展的序列化结构数据格式。

Protobuf对象描述文件为.proto类型，编译后生成.pb.h和.pb.cc文件。

Protobuf主要包含读写两个函数：Writer（序列化）函数SerializeToOstream() 和 Reader（反序列化）函数 ParseFromIstream()。

Tensorflow在core/probobuf目录中定义了若干与分布式环境相关的.proto文件，同时在core/framework目录下定义了与基本数据类型和结构的.proto文件，在core/util目录中也定义部分.proto文件，感觉太随意了。

在分布式环境中，不仅需要传输数据序列化，还需要数据传输协议。Protobuf在序列化处理后，由gRPC完成数据传输。gRPC数据传输架构图见图 3 14。

图 3 14 gRPC数据传输架构

gRPC服务包含客户端和服务端。gRPC客户端调用stub 对象将请求用 protobuf 方式序列化成字节流，用于线上传输，到 server 端后调用真正的实现对象处理。gRPC的服务端通过observer观察处理返回和关闭通道。

TF使用gRPC完成不同设备间的数据传输，比如超参数、梯度值、graph结构。

From: https://mp.weixin.qq.com/s/wyr1mUCX3aQaMrA-NsHN6g

TF - Graph模块

TF把神经网络模型表达成一张拓扑结构的Graph，Graph中的一个节点表示一种计算算子。

Graph从输入到输出的Tensor数据流动完成了一个运算过程，这是对类似概率图、神经网络等连接式算法很好的表达，同时也是对Tensor + Flow的直观解释。

5.1 Graph视图

Tensorflow采用符号化编程，形式化为Graph计算图。

Graph包含节点（Node）、边（Edge）、NameScope、子图（SubGraph），图 5 1是Graph的拓扑描述。

Ø 节点分为计算节点(Compute Node)、起始点（Source Node）、终止点（Sink Node）。起始点入度为0，终止点出度为0。

Ø NameScope为节点创建层次化的名称，图 3 4中的NameSpace类型节点就是其中一种体现。

Ø 边分为普通边和依赖边（Dependecy Edge）。依赖边表示对指定的计算节点有依赖性，必须等待指定的节点计算完成才能开始依赖边的计算。

图 5 1 Graph的拓扑描述

图 5 2是Graph的UML视图模型，左侧GraphDef类为protobuf中定义的graph结构，可将graph结构序列化和反序列化处理，用于模型保存、模型加载、分布式数据传输。右侧Graph类为/core/graph模块中定义的graph结构，完成graph相关操作，如构建(construct)，剪枝(pruning)、划分(partitioning)、优化(optimize)、运行(execute)等。GraphDef类和Graph类可以相关转换，如图中中间部分描述，函数Graph::ToGraphDef()将Graph转换为GraphDef，函数ConvertGraphDefToGraph将GraphDef转换为Graph，借助这种转换就能实现Graph结构的网络传输。

图 5 2 Graph的UML视图

Graph-UML图中还定义了Node和Edge。Node定义函数操作和属性信息，Edge连接源节点和目标节点。类NodeDef中定义了Op、Input、Device、Attr信息，其中Device可能是CPU、GPU设备，甚至是ARM架构的设备，说明Node是与设备绑定的。类FunctionDefLibrary主要是为了描述各种Op的运算，包括Op的正向计算和梯度计算。FunctionDef的定义描述见图 5 3。

图 5 3 FunctionDef的定义

图 5 4是FunctionDef举例，对MatMulGrad的梯度描述，其中包含函数参数定义、函数返回值定义、模板数据类型定义、节点计算逻辑。

图 5 4 FunctionDef举例：MatMulGrad

5.2 Graph构建

有向图（DAG）由节点和有向边组成。本章节主要讲述TF如何利用<Nodes, Edges>组合成完整的graph的。

假设有如下计算表达式：t1=MatMul(input, W1)。

图 5 5 Graph简单示例

图 5 5中图计算表达式包含：3个节点，2条边，描述为字符串形式如下。

TF先调用protobuf的解析方法将graph的字符串描述解析并生成GraphDef实例。

然后将GraphDef实例转化为tensorflow::Graph实例，这个过程由tensorflow::GraphConstructor类完成。GraphConstructor先判别node的字符串格式是否正确，然后执行convert函数。

首先，按拓扑图的顺序逐步添加node和edge到graph中。

然后，找出所有起始点（source node）和终止点（sink node）。

接着，对graph进行优化。图优化部分请参考章节6.5。

TF的graph构建模块测试用例在core/graph/graph_constructor_test.cc文件中。

5.3 Graph局部执行

Graph的局部执行特性允许使用者从任意一个节点输入（feed），并指定目标输出节点（fetch）。// <-- 对research很有帮助！

图 5 6是TF白皮书中描述Graph局部执行的图。[15]

图 5 6 Graph局部执行

图 5 6中左侧为计算图，如果要实现f=F(c)运算，代码如下：

result=sess.run(f, feed_dict={c: input})

TF是如何知道两个点之间的计算路径呢？这里涉及传递闭包的概念。

传递闭包就是根据graph中节点集合和有向边的集合，找出从节点A到节点B的最小传递关系。如上图中，点a到点f的传递闭包是a -> c -> f。

Graph局部执行过程就是找到feed和fetch的最小传递闭包，这个传递闭包相当于原graph的subgraph。代码文件在graph/subgraph.cc中，函数RewriteGraphForExecution()在确定feed节点和fetch节点后，通过剪枝得到最小传递子图。

剪枝操作的实现函数如下，Graph通过模拟计算流标记出节点是否被访问，剔除未被访问的节点。

5.4 Graph设备分配

TF具有高度设备兼容性，支持X86和Arm架构，支持CPU、GPU运算，可运行于Linux、MacOS、Android和IOS系统。而且，TF的设备无关性特征在多设备分布式运行上也非常有用。

Graph中每个节点都分配有设备编号，表示该节点在相应设备上完成计算操作。用户既可以手动指定节点设备，也可以利用TF自动分配算法完成节点设备分配。设备自动算法需要权衡数据传输代价和计算设备的平衡，尽可能充分利用计算设备，减少数据传输代价，从而提高计算性能。

Graph设备分配用于管理多设备分布式运行时，哪些节点运行在哪个设备上。TF设备分配算法有两种实现算法：

第一种是简单布放算法（Simple Placer）， // 按照指定规则布放，比较简单粗放，是早期版本的TF使用的模型，并逐步被代价模型方法代替

第二种基于代价模型（Cost Model）评估。

5.4.1 Simple Placer算法

TF实现的Simple Placer设备分配算法使用union-find方法和启发式方法将部分不相交且待分配设备的Op节点集合合并，并分配到合适的设备上。

Union-find（联合-查找）算法是并查集数据结构一种应用。并查集是一种树型的数据结构，其保持着用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。Union-find定义了两种基本操作：Union和Find。

Ø Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。

Ø Union：将两个子集合并成同一个集合。即将一个集合的根节点的父指针指向另一个集合的根节点。

启发式算法（Heuristic Algorithm）定义了节点分配的基本规则。Simple Placer算法默认将起始点和终止点分配给CPU，其他节点中GPU的分配优先级高于CPU，且默认分配给GPU:0。启发式规则适用于以下两种场景：

Ø 对于符合GeneratorNode条件（0-indegree, 1-outdegree, not ref-type）的节点，让node与target_node所在device一致，参见图 5 7。

图 5 7 启发式规则A

Ø 对于符合MetaDataNode条件（即直接在原数据上的操作，如reshape）的节点，让node与source_node所在device一致，参见图 5 8。

图 5 8 启发式规则B

TF中Simple Placer的实现定义在文件core/common_runtime/simple_placer.cc。文件中主要定义了两个类：ColocationGraph和SimplePlacer。ColocationGraph类利用Union-find算法将节点子集合合并成一个节点集合，参考成员函数ColocationGraph:: ColocateNodes实现。SimplePlacer类实现节点分配过程，下面将主要介绍SimplePlacer:: Run()函数的实现过程。