[Deep Learning] How deep is the Deep Learning - Reinforcement Learning

《王川: 深度学习有多深?》  - 阅读笔记

深度学习与增强学习

---

增强学习

除了前述的"有监督学习"，生活中大多数问题是没有标准正确答案的.你的所作所为,偶尔会得到一些时而清晰, 时而模糊的反馈信号. 这就是"增强学习" (Reinforcement Learning) 要解决的问题。

"增强学习"的计算模型,最核心的有三个部分:

1. 状态 (State): 一组当前状态的变量 (是否吃饱穿暖, 心满意足? 是郁郁寡欢, 还是志得意满? )

2. 行动 (Action): 一组可以采取的行动变量 (是努力工作, 还是游山玩水? 是修身养性, 还是夜夜笙歌? )

3. 回报 (Reward): 采取行动, 状态改变后,把当前获得的回报定量化. (喝酒就脸红, 吃多了就发胖, 大怒就伤肝, 工作超过八个小时身体就被掏空, 等等).

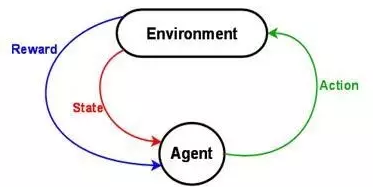
增强学习的最终目的,就是在和外界环境的接触/探索/观察的过程中,不断改进策略,把长期的回报/利益最大化而已.

 

贪心算法

增强学习的理论基础, 要从运筹学里的"贪婪算法" (Greedy Algorithm) 说起.

• • 贪婪算法的优点是容易理解，简单快速。但缺点是，
  • 得到的往往是局部最优解,而不是全球最优。

 

动态规划

动态规划,英文是 Dynamic Programming, 直译为"动态程序", 这个概念由美国数学家 Richard Bellman 在1950年提出。

它是在贪婪算法的基础上改进的算法. 实际上它和"动态","程序"两个概念没啥关系。

据 Bellman 老师介绍,当初为了忽悠政府的经费,就使用了"动态"这个词。动态，给人一种灵活,性感,高大上的感觉.谁会对"动态"说不?

（学术潜规则！）

 

动态规划算法的本质，是把一个复杂的问题拆分为多个子问题，并且把子问题的答案存储起来，避免以后的重复计算。

 

由于动态规划是从全局分析问题,所以往往可以找到全局最优解.但它的局限是,

第一，计算量大,需要穷举和存储子问题的解答方案.

第二，动态规划的隐藏的假设是一个叫做"最优化原理"的东西,就是说,最优化的解决方案,可以通过其子问题的最优解决方案获得. 换句话说,最优化问题的子决策,对于相应的子问题也是最优的.

什么样的问题不符合"最优化原理"?

一个典型的反例, 从点 A 到 点 B 的机票,最便宜的路线选择,是要到点 C 转机. 但从 A 到 C 最便宜的机票 (子问题), 却要从 点 D 再转机。

 

动态规划理论的核心, 用以 Richard Bellman 老师名字命名的 贝尔曼方程 (Bellman Equation)表示.

贝尔曼方程的核心, 就是:

 

用大白话说, 就是

目前状态的最大价值 = 最大化［ 眼前的回报 + ｛未来的最大价值，贴现到现在｝ ］

而动态规划要解决的问题，无非就是求解方程里的最优价值函数 V(x) 而已。

 

蒙特卡洛模拟

动态规划在实际操作上,最大的挑战就是所谓 "维度的诅咒" (Curse of Dimensionality)，就是随着变量的增加,问题的复杂度和计算量的需求,指数倍地增长.

一, 状态空间 (state space): 举个简单的例子, 医院的血液库管理中, 主要有八个不同类别的血型 (A+, A-, B+, B-, AB+, AB-, O+, O-), 而这些血液的存量数量从 0, 1, 到 M不等. 那么这个状态空间就有 M^8 种可能.

二, 结果空间 (outcome space): 还是以血液库的管理为例, 每周都有不同数量的不同血型的血液,被捐献或者输出.

三, 行为空间 (action space: ): 不同血型之间, 谁可以给谁输血,有几十种可能性.再加上血液库里每个血型的不同存量数目,行为空间之广阔,让人头大.

 

如果计算量太大,无法精致,那么退而求其次,我们就寻求"近似精致".

一个近似精致的解决思路,是所谓 "蒙特卡洛模拟" (Monte-Carlo Simulation).

MC 模拟优化的核心, 分两个部分: 

第一是计算模拟。

当没有简单的理论模型，维度的诅咒无法逾越时，

取而代之的是用计算机随机产生的参数，对可能的路径发展进行大规模模拟计算。

大量模拟之后，在各个状态节点,根据其模拟的平均值, 计算出一个接近理论值的预期价值函数.

第二是通用策略迭代 (Generalized Policy Iteration)。

根据模拟出来的价值函数，使用贪婪算法修正各个状态的策略,

也就是说，修正后的策略在每一步的选择 都是根据模拟的价值函数,寻求下一步的眼前利益最大化。

再根据调整的策略，回到第一步，重新模拟，更新价值函数。

 

两个步骤不断循环,渐进提高,直到接近最优值.

(如下图, V 代表价值函数, Pai 代表策略) 

 

 

关于 "通用策略迭代", 一个生活中的例子是,八十年代的宣传是"学好数理化,走遍天下都不怕",所以数理专业是当时大学生短期利益最大化的最优选择. 

但数学物理毕业生大多很难找到好工作,读 MBA 才可以有最高的薪水,许多人又纷纷跑去读 MBA.

拿到 MBA, 到大公司工作几年后,遇上金融危机,没攒什么钱又可能被解雇了.

过了几年再发现,有些刚毕业就去开公司的小毛孩,身价已经估值过亿.于是再改头换面,加入新的创业大潮。

 

MC 模拟的一个优点是,无须建模,完全根据实际经验来学习,容易上手.

毛主席曾说:“一些老粗能办大事。成吉思汗，是一个不识字的老粗。刘邦，也不认识几个字，是老粗。朱元璋也不认识字，是个放牛的。… ** 没念过书, ** 也没有念过书，** 念过高小, 结论是老粗打败黄埔生。”

 

这里的老粗,就像大量 MC模拟后的生成的实用性强的算法,没有生硬的理论培训,就在枪林弹雨中不断被淘汰,被选择,被教育. 而黄埔生则是被"维度的诅咒"束缚的动态规划的理论.

• • 但 MC 模拟算法的一个不足是, 学习和提高 (根据价值函数,更新策略) 是要在一个模拟的轮回, 岁月蹉跎之后才可以发生,而不能够实时进行. 
  • 在残酷的生存竞争中,需要的是一种更快的, 根据反馈来实时调整策略的能力.

 

这个算法的改进,启发来自于人脑多巴胺 (Dopamine)释放的机制。

 

时间差分学习

目的：近似最优价值函数。（人的价值判断体系）

研究的结论是: 多巴胺的释放,取决于获得的奖励和预期之间的差值，Delta。

现实和预期的差别, 促成了多巴胺的释放, 这是学习和进步的源动力。

时间差分学习 (Temporal Difference Learning, 下面简称为 TD学习) 思想的雏型, 上世纪五十年代就被不同的学者提出.

它的核心思想, 就是在每个时间点通过计算现实和预期的差值,来微调价值函数值. 这和大脑多巴胺释放的机制,不谋而合。

 

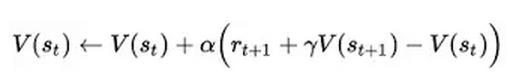
它与蒙特-卡洛(MC)模拟的区别在于：

• • MC 模拟要在一个轮回之后,再更新各个节点的价值函数。
  • TD 是在每个时间点, 根据观察到的结果不断评估,微调。

 

打个简单的比方,如果把"过河"作为一个要解决的问题：

• • 动态规划的解决办法,就是耗费大量时间测算河水的深浅,河里的石头大小,分布,然后计算最优的过河方案. 它的缺点是耗时过长, 很可能方案算出来的时候,你的孙子都已经出生了.
  • MC 模拟，就好比派一大群志愿者强行渡河,有些人在渡河中会摔跤甚至淹死,但经过大量先烈前赴后继的实验后,也可以找到最佳方案。
  • TD 算法,就是"摸着石头过河"。

 

TD 算法真正名声大噪, 要到 1992年, 在一个古老游戏上的应用。

 

迄今为止关于各种算法的讨论，都离不开一个核心概念： 价值函数. （人的价值判断体系）

简单说，在贝尔曼方程里面，价值函数就是目前状态的理论最大值。

如何近似价值函数？精确计算的话运算量过大，比如围棋。

 

1992年，IBM的研究员 Gerald Tesauro 开发了一个结合时间差分学习 （TD Learning）和神经网络的算法，给它取名 TD-Gammon,  专攻双陆棋。

（用神经网络近似价值函数，你是好派？还是P派？）

TD-gammon 使用了一个三层神经网络，如下图，

• • 输出值是价值函数的估算，
  • 中间的隐层有40-80个神经元，
  • 棋盘状态由198个神经元代表，为输入端。

 

TD-gammon 最初版本，中间的隐层只有40个神经元，通过自己和自己下棋提高水平。

每走一步，用时间差分算法，根据价值函数估算的差值，重新微调神经网络的参数。(每走一步，都有好与坏的概念，细致地讲，好多少，坏多少)

经过三十万个棋局的自我训练后，它达到了此前表现最好的电脑程序的水平。甚至，TD-gammon 的另外一个收获是，在开局的落子上，发现了另外一种被所有前人忽略的走法，比传统走法要略优。

 

在用神经网络计算拟合最优价值函数 (最大利益）的实践中，最大的挑战，就是神经网络的参数无法收敛到最优值，甚至变得发散。

• • 这个问题的第一个原因, 增强学习在和环境互动的过程中, 获得的数据都是高度相关的连续数列。当神经网络依靠这些数据来优化时，存在严重的样本偏差。
  • 这个问题的第二个原因，在于神经网络对于价值函数的估算值极为敏感。 如果价值函数值出现波动，会直接影响到在和环境互动，学习的过程中收集到的新的数据样本，进而影响神经网络参数的巨大波动而无法收敛。
  • 这个问题的第三个原因，在于价值函数值的范围，事前很难有正确的估计。

 

其中俩问题的解决，as following。

在增强学习领域，经历 (experience) 是指四个参数的集合：

• (x, a, y, r) 表示在状态 x, 做了 a, 进入了新的状态 y, 获得了回报 r。
• 教训 (lesson) 则是指一个时间序列的经历的集合。

 

经历回放 (experience replay) 的概念由 Long Ji Lin 在 1993年的博士论文里第一次提出。

"经历回放" 的第一个好处是更有效率。经验教训，尤其是有重大损失的经验教训，是昂贵的，如果把它存储到记忆里，可以日后反复调用学习，那么学习效率就会大大提高, 不用吃二遍苦，受二茬罪.

于介绍过的神经网络的“长短期记忆” (Long Short-term memory) 有异曲同工之妙。

 

”经历回放“在增强学习的计算中是这样实现的:

在环境中学习积累的数据 （x, a, y, r) 被不断存储到一个数据集里.

每一次对神经网络的参数进行更新时，就从数据集里随机地调取一小批”经历“，帮助培训神经网络.

"经历回放"样本的随机性，彻底解决了价值函数发散的两个原因：

• • 第一, 每次用于培训的一小批“经历”不再是连续相关的数据。这就好比一个小白投资者可以同时见证学习牛市，熊市，猪市和猴市， 跳出了他生活时代的历史局限.
  • 第二, 每次用于培训的“经历”不再受价值函数波动对环境的影响，这就好比股票投资者在股市时髦的时候，仍然有机会全面地学习房市，债市，外汇, 期权, 期货，风险投资等其它领域的知识，跳出了他工作环境的局限.

 

经验也有座次，as following。

实际操作上，不管是人还是机器, "经历"的数据集的大小是有限制的。如果积累的数据超过这个限制，不得不将老的数据扔掉，给新的数据腾出空间。

不是所有的经历的记忆，都有同样的价值。算法上如何管理有限的记忆，给有些经历更多的优先权，是一个重要的问题.

一个改进的算法，所谓“优先化经历回放", (Prioritized Experience Replay) , 是把各类经历按照所谓的时间误差 (Temporal Difference Error) 来排序，误差绝对值越大的经历，日后被重新调用的几率也就更大。

 

深度-Q-网络

"突围" 游戏的规则很简单：显示屏上八层砖头，每两层是同一种颜色， 总共分黄，绿，桔，红四色。玩家用板子击球，球碰倒砖头后就得分。不同颜色的砖头得分各不相同。如果来球没有被接到，就丢掉一个回合。球的速度随着击打次数的增加也不断增加。

最终目的是在三个回合内获得最高分.

2013年12月，总部在伦敦的 Deepmind 公司的团队发表论文：Playing Atari with Deep Reinforcement Learning （"使用深度增强学习玩Atari 电脑游戏"）, 详细地解释了他们使用改进的神经网络算法在包括 Atari Breakout 在内的电脑游戏的成果.

Deepmind 算法设计时，把电脑游戏的最新的四帧屏幕，作为神经网络的输入。每帧屏幕用 84 x 84 的像素表征.

除了获得的分数以外，没有任何人为输入的游戏规则的信息。全靠长期培训，让机器自己悟出，什么是最佳的策略.

 

神经网络有三个隐层，

• • 其中有两个卷积层 （convolution layer), 用于过滤和提取像素中的局部特征。
  • 第三层是一个全连接层 (Fully connected layer)， 针对游戏中每一个瞬间玩家可能采取的行动选择 （大约有 4-18个行动选择），输出相应的价值函数的估算。

不同行动选择的回报值，就是所谓的 Q-value. 神经网络的培训，就是要拟合 Q-value，用于计算如何选择利益最大化的行动. 这个用三层神经网络学习打游戏的模型，就叫 Deep-Q-Network (深度-Q-网络， 简称 DQN).

DQN 的参数初始值，完全随机化，就像一个新入行，两眼一抹黑的小白。但开始不懂没关系，最重要的，是自我学习新技能的速度。

 

在增强学习和运筹学里一个经典问题是选择”勘探还是开发“ （exploration or exploitation) . 换言之，是仅仅根据现有的信息把利益最大化，还是花一部分时间去探索外面的世界是否更精彩.

解决这个问题的通行做法，是所谓的 epsilon-greedy strategy, 这里翻译为 "有时不贪婪的策略". 这个策略，就是大部分时间贪婪 (根据现有信息寻求利益最大化)，但是还有 epsilon 的几率去做一些完全随机的探索 （有时不贪婪）.

• • 埋头读书工作，固步自封的人，epsilon = 0, 这是传统的贪婪策略.
  • 天天到处乱晃，东一榔头西一棒子的人， epsilon = 1.

这两个极端都不好；有时不贪婪，做一些短期的牺牲，是为了长期的贪婪和利益最大化。如何把握 epsilon 这个度，是个挑战。

DQN 的 epsilon 的初始值为 1,以随机探索为主, 经过一百万帧的培训后慢慢降到 0.1 不变, 也就是始终保持 10%的时间随机探索。

 

对于一个 60 赫兹的显示屏而言，一秒钟是 60帧，一百万帧就相当于约四个多小时的游戏时间。

DQN 在拟合神经网络参数的计算时，使用了上篇文章提到的 “经历回放”的技巧，用于存储经历的空间达到一百万帧.

DQN 的算法，用大白话来说，是这样的:

神经网络参数随机初始化 （刚出道，什么都不懂，无知者无畏）
把下面的循环重复 N 遍：

从 1 到 T 时间
以 epsilon 的几率随机探索

否则, 选择现有认知下, 利益最大化的行动 a(t)

干 a(t), 完事后记下回报 r(t), 和新状态 s(t+1)
把刚才的经历写入记忆，用于以后回放 （获得了经验）

从记忆中随机提取部分经历，
通过随机梯度下降的计算方法，优化拟合神经网络的参数（优化了经验）

  

经过长期培训后的 DQN, 打电脑游戏时的表现，让程序设计者也大吃一惊：（值得实践）

• 刚开始, 不了解游戏规则的程序，表现得像个无头苍蝇，老是漏球.
• 经过10分钟的训练后，慢慢懂得要用板子击球，才可以得分.
• 经过120分钟的训练后，程序可以迅速准确击球，表现得有点专家的味道了.
• 经过240分钟的训练后，程序发现了一个获得高分的捷径:
  1. 不断用板子击球到最左边，
  2. 连续数次后左边的几层砖头全部击倒打通，
  3. 随后击球就可以经过这个隧道绕到墙的后面，
  4. 在墙壁后面多次连续反弹击倒一大片砖头，获得高分。

这个精巧的打法，是程序设计者事前完完全全没有想到的！

 

在训练过程中还有这样一个问题，由于算法在决策过程中总是有一定几率的随机探索，每局游戏的比分总是有些随机的波动。

对于一个普通观察者来说，在一个较短的时间段内，他只看到每局得分大起大落，但无法准确判断程序是否真正学到了东西，有技能的提高.

这里对于价值函数最大值 Q-value 的估算就派上用场了, 如下图.

• • 左边两图是程序在多次培训后平均得分的曲线图。对于旁观者而言，图中的右半部波动较大，看不出得分有什么进步。  
  • 右边两图，则是神经网络对 Q-value 的估值，这个数字，则是一直缓缓上升的。

 

这里面有个非常深刻的洞见：

如果人们总是让人生旅程上短期的得失，尤其是因为偶然不可控因素导致的得失，影响情绪上的波动，那么精神状态就会象左边两张图一样忽上忽下，而随之而来的狂躁症，忧郁症，双向情感障碍，也就成为必然.

但如果树立了科学的方法论和价值观，可以正确地估算 Q-value, 面对短期的大起大落，知道自己实际上是在不断进步，知道未来在变得更好，知道短期的挫折或者成就以后不值一提，所以可以拒绝一惊一乍，所以可以坚持平心静气.　　

所谓宠辱不惊，原来无非如此。

(上述感受不谋而合)

 

回头看，如果要总结为什么机器打游戏彻底超越人类玩家，主要原因还是三点: 

第一，计算能力的大幅度提升，这是最根本的.

和在西洋双陆棋上实现突破的 1992年时相比，2013年的使用 GPU的计算能力至少增加了几十万倍。只有这样的计算能力，才能够处理复杂的神经网络模型和海量的输入数据.

第二， 算法的改进

这里，主要是深度神经网络，经历回放和传统增强学习的理论模型的结合。

第三，由于计算速度的提高，和算法的改进，机器有能力探索更广阔的状态空间，从而有能力发现人类从未感知的一个全新的世界.

更重要的是，和图像识别，语音识别这类有明确标准答案的问题不同，这一次，程序设计者甚至都没有设定任何明确的游戏规则，只有游戏屏幕的原始像素的输入，和游戏得分的回馈，其它一切让机器自己去摸索.

然后机器发现了比人类更好的打法.

这让学者们看到了实现真正的 “强人工智能”, (机器自发解决以前只有人类才可解决的抽象问题）的希望.

 

机器超越人的智能，本质上也无非就是 算得更快，记得更多，更善于探索 而已。

 

2014年一月，谷歌宣布以五亿美元收购 Deepmind. 对于大多数吃瓜群众而言，一个没有什么收入，就是写了个可以打游戏的程序的公司, 估值五亿，完全不可思议。

吃瓜群众焉知人工智能之志哉？ 

有诗为证: “飞来山上千寻塔，闻说鸡鸣见日升，不畏浮云遮望眼，自缘身在最高层"。