[Optimized Python] "Generator": calculating prime
高性能编程
几个核心问题
• 生成器是怎样节约内存的?
• 使用生成器的最佳时机是什么?
• 我如何使用 itertools 来创建复杂的生成器工作流?
• 延迟估值何时有益,何时无益?
From: https://www.dataquest.io/blog/python-generators-tutorial/
• The basic terminology needed to understand generators
• What a generator is
• How to create your own generators
• How to use a generator and generator methods
• When to use a generator
表示数列
有限数列情况
案例一:xrange,节省内存
自定义xrange使用yield,采用的方法是依次计算。
目前的range具备了这个特性。
In [16]: def xrange(start, stop, step=1): ...: while start < stop: ...: yield start ...: start += step ...: In [17]: for i in xrange(1,100): ...: print(i)
无限数列情况
案例二:Fibonacci Sequence
def fibonacci(n): a, b = 0, 1 while n > 0: yield b a, b = b, a + b n -= 1 def Fibonacci_Yield(n): # return [f for i, f in enumerate(Fibonacci_Yield_tool(n))] return list(fibonacci(n))
案例三:fibonacci中有几个奇数
for 循环中的自定义序列。
def fibonacci_transform(): count = 0 for f in fibonacci(): if f > 5000: break if f % 2 == 1: count += 1 return count
生成器的延时估值
—— 主要关注如何处理大数据,并具备什么优势。
Ref: Python Generators
Big Data. This is a somewhat nebulous term, and so we won’t delve into the various Big Data definitions here. Suffice to say that any Big Data file is too big to assign to a variable.
尤其是List不方便一下子装载到内存的时候。
各种形式的生成器
- Load beer data in big data.
beer_data = "recipeData.csv"
lines = (line for line in open(beer_data, encoding="ISO-8859-1"))
建议把这里的open事先改为:with ... as。
- Laziness and generators
Once we ask for the next value of a generator, the old value is discarded.
Once we go through the entire generator, it is also discarded from memory as well.
进化历程
- Build pipeline
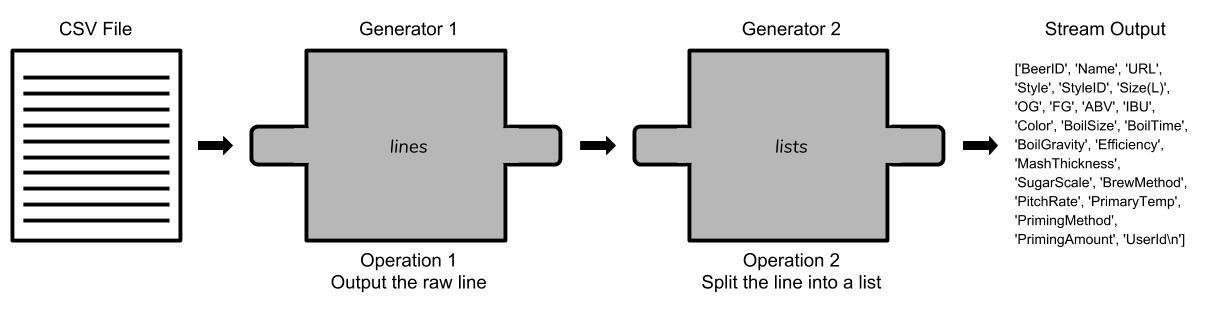
beer_data = "recipeData.csv"
lines = (line for line in open(beer_data, encoding="ISO-8859-1")) # (1) 获得了“一行” lists = (l.split(",") for l in lines) # (2) 对这“一行”进行分解
- Operation in pipeline
(1) 先获得第一行的title,也就是column将作为key;然后从第二行开始的值作为value。
['BeerID', 'Name', 'URL', ..., 'PrimaryTemp', 'PrimingMethod', 'PrimingAmount', 'UserId\n']
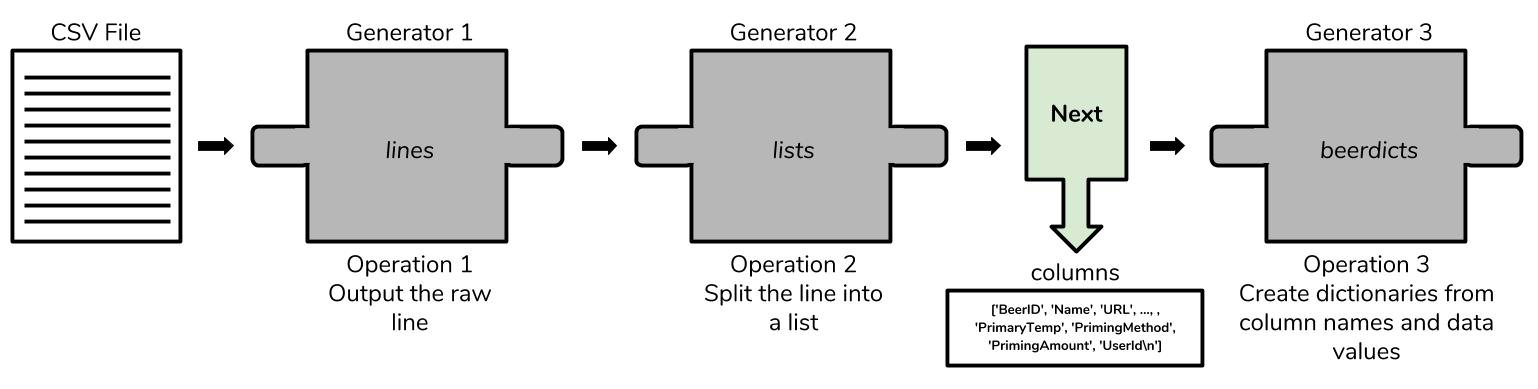
zip()将两个list的元素配对,然后转换为dict。
# 样例模板
beer_data = "recipeData.csv"
lines = (line for line in open(beer_data, encoding="ISO-8859-1")) lists = (l.split(",") for l in lines)
#-----------------------------------------------------------------------------
# Take the column names out of the generator and store them, leaving only data columns = next(lists) # 取第一行单独出来用 # Take these columns and use them to create an informative dictionar beerdicts = ( dict( zip(columns, line) ) for line in lists )
(2) 一行数据结合一次“标题栏” 构成了一条新的数据。然后,开始统计。
bd["Style"] 作为每一条数据的类别的key,拿来做统计用。

# 遍历每一条,并统计beer的类型 beer_counts = {} for bd in beerdicts: if bd["Style"] not in beer_counts: beer_counts[bd["Style"]] = 1 else: beer_counts[bd["Style"]] += 1 # 得到beer类型的统计结果:beer_counts most_popular = 0 most_popular_type = None for beer, count in beer_counts.items(): if count > most_popular: most_popular = count most_popular_type = beer most_popular_type >>> "American IPA"
# 再通过这个结果,处理相关数据 abv = (float(bd["ABV"]) for bd in beerdicts if bd["Style"] == "American IPA")
质数生成 - prime number
next 结合 yield
定义了一个“内存环保”的计算素数的函数primes()。
def _odd_iter(): n = 1 while True: n = n + 2 yield n
# 保存一个breakpoint,下次在此基础上计算
def _not_divisible(n): return lambda x: x % n > 0
# 对每一个元素x 都去做一次处理,参数是n
def primes(): yield 2 it = _odd_iter() # (1).初始"惰性序列"
while True: n = next(it) # (2).n是在历史记录的基础上计算而得 yield n it = filter(_not_divisible(n), it) # (3).构造新序列,it代表的序列是无限的;
p = primes()
next(p)
next(p)
这里妙在,在逻辑上保证了it代表的序列是个无限序列,但实际上在物理意义上又不可能。
例如,当n = 9时?首选,n不可能等于9,因为后面会“不小心”yield出去。
闭包带来的问题
Stack Overflow: How to explain this “lambda in filter changes the result when calculate primes"
此问题涉及到 Lambda如何使用,以及闭包的风险:[Python] 07 - Statements --> Functions
# odd_iter = filter(not_divisible(odd), odd_iter) # <--(1) odd_iter = filter((lambda x: x%odd>0) , odd_iter) # <--(2)
当yield的这种lazy机制出现时,谨慎使用lambda;注意保护好”内部变量“。
质数生成的"高效方案"
# Sieve of Eratosthenes # Code by David Eppstein, UC Irvine, 28 Feb 2002 # http://code.activestate.com/recipes/117119/ def gen_primes(): """ Generate an infinite sequence of prime numbers. """ # Maps composites to primes witnessing their compositeness. # This is memory efficient, as the sieve is not "run forward" # indefinitely, but only as long as required by the current # number being tested. # D = {} # The running integer that's checked for primeness q = 2 while True:
if q not in D: # q is a new prime. # Yield it and mark its first multiple that isn't # already marked in previous iterations # yield q D[q * q] = [q] else: # q is composite. D[q] is the list of primes that # divide it. Since we've reached q, we no longer # need it in the map, but we'll mark the next # multiples of its witnesses to prepare for larger # numbers # for p in D[q]: D.setdefault(p + q, []).append(p)
print("else: {}, {}".format(q, D))
del D[q] q += 1
... loop: 2, {} 2 loop: 3, {4: [2]} 3 loop: 4, {4: [2], 9: [3]} else: 4, {4: [2], 9: [3], 6: [2]} loop: 5, {9: [3], 6: [2]} 5 loop: 6, {9: [3], 6: [2], 25: [5]} else: 6, {9: [3], 6: [2], 25: [5], 8: [2]} loop: 7, {9: [3], 25: [5], 8: [2]} 7 loop: 8, {9: [3], 25: [5], 8: [2], 49: [7]} else: 8, {9: [3], 25: [5], 8: [2], 49: [7], 10: [2]} loop: 9, {9: [3], 25: [5], 49: [7], 10: [2]} else: 9, {9: [3], 25: [5], 49: [7], 10: [2], 12: [3]} loop: 10, {25: [5], 49: [7], 10: [2], 12: [3]} else: 10, {25: [5], 49: [7], 10: [2], 12: [3, 2]} loop: 11, {25: [5], 49: [7], 12: [3, 2]} 11 loop: 12, {25: [5], 49: [7], 12: [3, 2], 121: [11]} else: 12, {25: [5], 49: [7], 12: [3, 2], 121: [11], 15: [3]} else: 12, {25: [5], 49: [7], 12: [3, 2], 121: [11], 15: [3], 14: [2]} loop: 13, {25: [5], 49: [7], 121: [11], 15: [3], 14: [2]} 13 loop: 14, {25: [5], 49: [7], 121: [11], 15: [3], 14: [2], 169: [13]} else: 14, {25: [5], 49: [7], 121: [11], 15: [3], 14: [2], 169: [13], 16: [2]} loop: 15, {25: [5], 49: [7], 121: [11], 15: [3], 169: [13], 16: [2]} else: 15, {25: [5], 49: [7], 121: [11], 15: [3], 169: [13], 16: [2], 18: [3]} loop: 16, {25: [5], 49: [7], 121: [11], 169: [13], 16: [2], 18: [3]} else: 16, {25: [5], 49: [7], 121: [11], 169: [13], 16: [2], 18: [3, 2]} loop: 17, {25: [5], 49: [7], 121: [11], 169: [13], 18: [3, 2]} 17 loop: 18, {25: [5], 49: [7], 121: [11], 169: [13], 18: [3, 2], 289: [17]} else: 18, {25: [5], 49: [7], 121: [11], 169: [13], 18: [3, 2], 289: [17], 21: [3]} else: 18, {25: [5], 49: [7], 121: [11], 169: [13], 18: [3, 2], 289: [17], 21: [3], 20: [2]} loop: 19, {25: [5], 49: [7], 121: [11], 169: [13], 289: [17], 21: [3], 20: [2]} 19 loop: 20, {25: [5], 49: [7], 121: [11], 169: [13], 289: [17], 21: [3], 20: [2], 361: [19]} else: 20, {25: [5], 49: [7], 121: [11], 169: [13], 289: [17], 21: [3], 20: [2], 361: [19], 22: [2]} loop: 21, {25: [5], 49: [7], 121: [11], 169: [13], 289: [17], 21: [3], 361: [19], 22: [2]} else: 21, {25: [5], 49: [7], 121: [11], 169: [13], 289: [17], 21: [3], 361: [19], 22: [2], 24: [3]} loop: 22, {25: [5], 49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 22: [2], 24: [3]} else: 22, {25: [5], 49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 22: [2], 24: [3, 2]} loop: 23, {25: [5], 49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 24: [3, 2]} 23 loop: 24, {25: [5], 49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 24: [3, 2], 529: [23]} else: 24, {25: [5], 49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 24: [3, 2], 529: [23], 27: [3]} else: 24, {25: [5], 49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 24: [3, 2], 529: [23], 27: [3], 26: [2]} loop: 25, {25: [5], 49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 529: [23], 27: [3], 26: [2]} else: 25, {25: [5], 49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 529: [23], 27: [3], 26: [2], 30: [5]} loop: 26, {49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 529: [23], 27: [3], 26: [2], 30: [5]} else: 26, {49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 529: [23], 27: [3], 26: [2], 30: [5], 28: [2]} loop: 27, {49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 529: [23], 27: [3], 30: [5], 28: [2]} else: 27, {49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 529: [23], 27: [3], 30: [5, 3], 28: [2]} loop: 28, {49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 529: [23], 30: [5, 3], 28: [2]} else: 28, {49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 529: [23], 30: [5, 3, 2], 28: [2]} loop: 29, {49: [7], 121: [11], 169: [13], 289: [17], 361: [19], 529: [23], 30: [5, 3, 2]} 29
End.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号