[ML] Bayesian Linear Regression

热身预览

1.1.10. Bayesian Regression

 

From: scikit-learn 线性回归算法库小结

17. BayesianRidge

使用场景：

如果我们的数据有很多缺失或者矛盾的病态数据，可以考虑BayesianRidge类，它对病态数据鲁棒性很高，也不用交叉验证选择超参数。但是极大化似然函数的推断过程比较耗时，一般情况不推荐使用。

 

18. ARDRegression

ARDRegression和BayesianRidge很像，唯一的区别在于对回归系θ的先验分布假设。

    • BayesianRidge假设θ的先验分布规律为球形正态分布，BayesianRidge中球形分布的θ对应的λ只有一个。
    • ARDRegression丢掉了BayesianRidge中的球形高斯的假设，采用与坐标轴平行的椭圆形高斯分布。这样对应的超参数λ有n个维度，各不相同。

ARDRegression也是通过最大化边际似然函数来估计超参数α和λ向量，以及回归系数θ。

使用场景：

如果我们的数据有很多缺失或者矛盾的病态数据，可以考虑BayesianRidge类，如果发现拟合不好，可以换ARDRegression试一试。

因为ARDRegression对回归系数先验分布的假设没有BayesianRidge严格，某些时候会比BayesianRidge产生更好的后验结果。

 

 

 

贝叶斯线性拟合

一、解题思路

总感觉 贝叶斯回归能更好的“拟合”，真的嚒？

总体思路依然是：(1) 找到最大似然 (2) 通过EM找到渐近解，或者通过“增量学习”进行“training"。

Ref: 贝叶斯线性回归（Bayesian Linear Regression）

 

二、贝叶斯估计的增量学习（在线学习方法）

详见链接：贝叶斯线性回归（Bayesian Linear Regression）

增量方法：基于贝叶斯推断的回归模型（代码篇）： 机器学习你会遇到的“坑” 

贝叶斯线性估计，它的基本思想是通过增量学习，将上一个数据点的后验概率作为下一次的先验概率，并使用全部的数据点通过极大后验估计来估计参数值。

 

三、贝叶斯线性估计示范

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import timefrom sklearn.linear_model import BayesianRidge, LinearRegression

X = [[1,1], [1,2], [1,3], [1,4], [1,5], [1,6]]
y = [25, 36, 45, 54, 72, 83]

print(X)
print(y)

###############################################################################
# 使用贝叶斯脊回归拟合数据
clf = BayesianRidge(compute_score=True)
clf.fit(X, y)

print(clf.predict([[1,7]]))
print(clf.coef_)

X_test=[[1, 1],  [1, 2],  [1, 3],  [1, 4],  [1, 5],  [1, 6], [1, 7]]
y_pred = clf.predict(X_test)

# Plot outputs
plt.scatter([1,2,3,4,5,6], y,  color='black')
plt.plot([1,2,3,4,5,6,7], y_pred, color='blue', linewidth=3)

plt.xticks(())
plt.yticks(())plt.show()

 

 

 

增量在线学习

 

一、参数估计方法论

常用的参数估计方法有：极大似然估计 ----> 最大后验估计 ----> 贝叶斯估计 ----> 最大熵估计 ----> 混合模型估计。

他们之间是有递进关系的，想要理解后一个参数估计方法，最好对前一个参数估计有足够的理解。

极大似然估计

将θ看做是未知的参数。

最大后验估计

参数θ 看成一个随机变量。

贝叶斯估计

参数θ的后验分布的期望。

 

二、增量学习过程

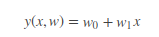
这个式子也算是 “高维线性可分” 的最简单的版本。

重点理解第二行的由来，先承认一个重要的认知：

    • x, y是样本，自然是确定的数据。
    • w是参数，我们理解为是“随机变量”，是需要估计的东西；先假设是标准的二维高斯分布。

  

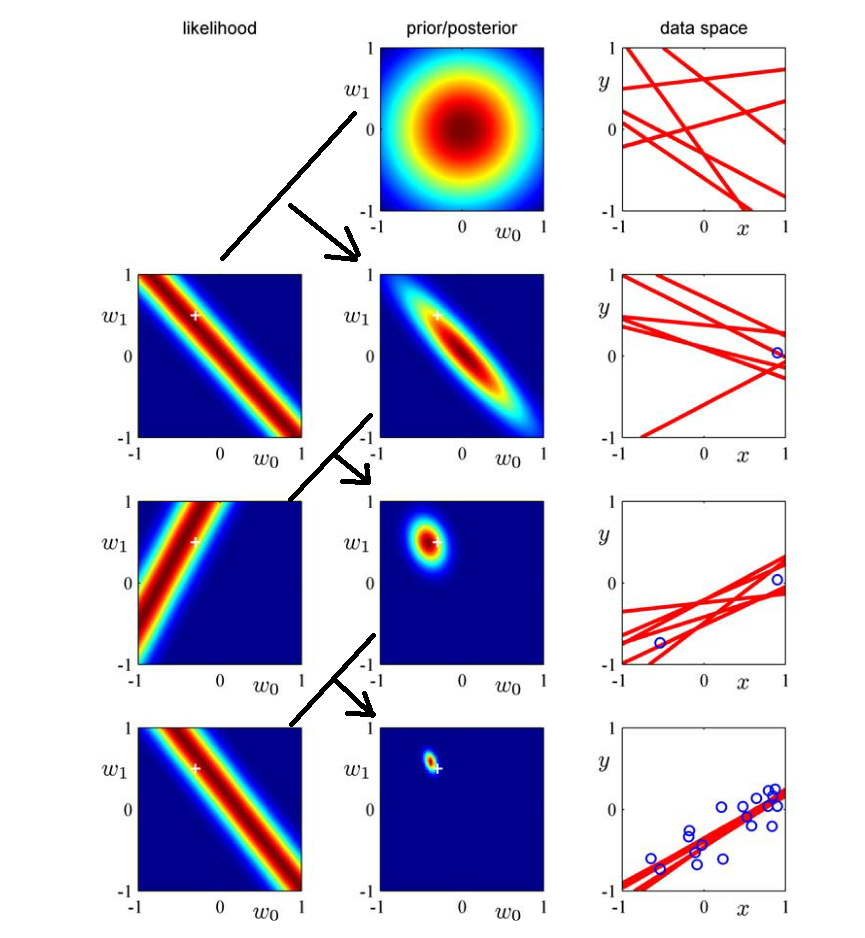
（1）第一个样本点的坐标大概为:(0.9,0.1) --> 得到如下式子，也就是“第二行左图”。【得到一个样本，对参数做出调整】

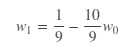
（2）将第二行的第左边那幅图和第一行的中间那幅图相乘，就可以得到第二行中间那幅图。【这是参数的分布，方差在逐渐减小】

（3）第二行最右边那幅图就是从第二行中间那幅图中随机抽取一些点(w0,w1)，并以(w0,w1)为参数，画出来的直线。【这些红色直线，之后会收敛】

 

优点： 

1. 贝叶斯回归对数据有自适应能力，可以重复的利用实验数据，并防止过拟合。
2. 贝叶斯回归可以在估计过程中引入正则项。


缺点： 

1. 贝叶斯回归的学习过程开销太大。

 

 

 

增量EM算法

Ref: EM算法及其改进

EM的缺点：收敛缓慢；一次迭代遍历所有样本，太费事儿。

 

 

online learning的一种，类似"反向传播算法”的效果。

这跟sampling估产的原理有啥区别？ 难道没有上述缺点？

 

 

 

MCMC采样估参

Ref: [Bayes] Parameter estimation by Sampling

Ref: 贝叶斯网与吉布斯采样学习心得(之零，兼引言)

 

贝叶斯网络 (Baysian Network)

贝叶斯网络(Baysian Network)是统计推断中的重要工具。简单地说，贝叶斯网就是对于由一系列待估计量作为自变量的联合分布的一种描述。即贝叶斯网描述了如下的后验分 [公式]


其中[公式]代表一个待估计变量构成的向量，[公式]为一系列的已知测量量。原则上讲，如果我们能够写出[公式]的具体表达式，我们就能给出关于[公式]的统计特征的描述，从而直接求解这一统计推断问题。

如果必要，在贝叶斯的框架下，我们可以将这一后验概率进一步展开为：

 [公式]  ----> 即先验概率[公式]和似然函数[公式]的乘积。

 

问题来了

如果我们有后验概率的具体表达式，原则上我们可以对待估计变量[公式]的统计特征进行直接估计。然而现实并不那么美好！

 

如果[公式]的维度很高，而且后验概率形式特别复杂，往往导致在对[公式]的某个分量求解边缘分布时的积分无法简单直接求得。

例如，求某个分量的期望就必然涉及对后验概率的积分。

蒙特卡罗积分法对于高维度的积分问题而言是一种可行的解决方案，基于这一原理，我们就能用基于抽样的方法来解决这一问题（这里的抽样是指按照给定的联合分布产生一个符合该分布的样本，而不是指从一个总体中抽取出一个样本）。
如果我们能够对后验概率进行采样，即根据后验概率获得一系列 [公式]的实现样本，我们就能够对这个样本进行直接的统计，从而获得对[公式]的估计。

 

那么如何完成对[公式]的采样呢？这时候我们便要请出吉布斯(Gibbs)采样算法了。

吉布斯采样算法的基本思想很直接，就是依次对[公式]的各个分量进行采样，在采样某一个分量的时候，认为其他分量固定。这就将多维采样问题转换为了对一维分布进行采样，而这能够用拒绝算法(或者自适应拒绝算法)、切片法等等解决。

 

改善采样效率

本来故事到这里已经可以结束，从而没有贝叶斯网什么事情了，但是实践中，我发现(当然不可能是我首先发 现的)，直接对后验概率进行吉布斯采样，虽然能凑合着用，但是效率有时候堪忧，贝叶斯网的出现可以显著改善采样的效率。

如果我们能够把后验概率进行分解， 把各个参量之间的关系捋顺，在对某一具体分量进行采集的时候，只需要计算和它相关的量，就能大大降低计算复杂性，从而提高效率。

End.

posted @ 2019-07-27 08:39  郝壹贰叁  阅读(934)  评论(0)  编辑  收藏  举报