数据结构(直接寻址表、hash表,树结构)
线性结构,树结构,图结构
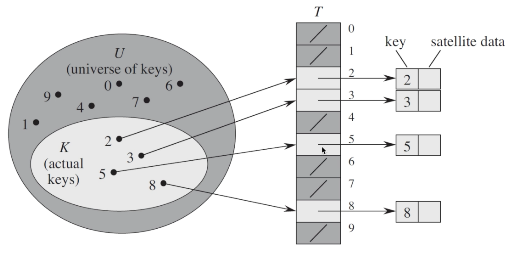
直接寻址表
- 直接寻址表,定义了一个所有关键字的域集合U,根据这个U生成一个包含所有域值的列表T
- 直接寻址技术优点:
- 当数据量较小时,操作相对简单有效
- 直接寻址技术缺点:
- 当U很大时,建立列表T,所消耗的内存空间非常大
- 如果U非常大,而实际出现的key非常少,这样就对空间造成了极大的浪费
- 当关键字key不是数字的时候就无法处理了
hash(哈希)
- 基本概念:hash,也称作散列、杂凑或者哈希,是一种线性表的存储结构。哈希表由一个直接寻址表和一个哈希函数组成,哈希函数h()将元素的关键字k处理得到唯一的存储元素的位置信息。能把任意长度的输入,通过hash算法转化为固定长度的输出,是一种压缩映射。最大的特点就是从无法从结果推算出输入内容,所以称之为不可逆算法。本质上是通过哈希函数计算数据存储位置的数据结构。
- python中的字典和集合就是利用哈希表实现的。
- hash表是对直接寻址表的改进,具体的
- 构建大小为m的寻址表T,[0,1,2,3,……,m-1]
- 将关键字为k的元素,放置在T中的 h(k)所指定的位置上,这里不是直接用k作为键进行存储,而是使用h(k)
- h() 是哈希函数,将U中的key映射到寻址表T中
- 一个简单的除法哈希表
- 哈希特性:
- 过程不可逆,即拿到结果也不能反解出输入值是多少
- 计算速度极快
- 哈希表存在的问题:
- 哈希冲突
- 由于关键字的数量是无限的,而hash创建的寻址表T是有限的,所以必定会出现存储位置冲突或重复,即当h(k)和h(k1)的值相同时,两个值的存储位置是冲突的。
- 哈希冲突的解决方式:
- 方式一:开放寻址法,如果哈希函数返回的位置已经有值,则继续向后探寻新的位置来存储这个值。而继续向下探寻位置的方法有
- 线性探查,如果位置i被占用,则向下探查i+1,i+2 ……直至空位置
- 二次探查,如果位置i被占用,则依次探查i+1^2,i+2^2……直至空位置
- 二度哈希:有n个哈希函数,等使用第一个哈希函数h1,发生冲突时,依次尝试使用h2,h3……
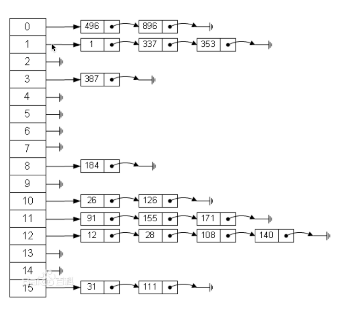
- 方式二:拉链法,哈希表每个位置都链接一个链表,当冲突发生时,冲突的元素被加到该位置链表后面
-
- 方式一:开放寻址法,如果哈希函数返回的位置已经有值,则继续向后探寻新的位置来存储这个值。而继续向下探寻位置的方法有
- 哈希冲突
- 常见的哈希函数:
- 除法哈希: h(k)=k%m
- 乘法哈希:h(k) = floor(m*(A*key%1))
- 全域哈希:h(k) = ((a*key+b) mod p) mod m a,b =1,2,……p-1
- hash表的基本操作:
- insert(key,value) 插入键值对
- get(key) 根据键取值
- delete(key) 删除键值对
- 主要的应用方向:
- python等语言的字典、集合等数据类型就是基于hash实现的
- 密码,很多密码都是基于hash构造出来的
- 可以用于检测文件的一致性
- 用于数字签名
- MD5,SHA-1,SHA-2
- hash表的简单实现(拉链法,单链表)
-
![]() View Code
View Code1 """ 2 使用链表,实现hash。构建一个类似于集合的hash表 3 """ 4 class LinkList(object): 5 """ 6 对链表的进一步封装 7 """ 8 class Node(object): 9 """ 10 链表的节点类 11 """ 12 def __init__(self,item): 13 self.item = item 14 self.next = None 15 16 class LinkListIterator(object): 17 """ 18 将链表转为迭代器类 19 """ 20 def __init__(self,node): 21 self.node = node 22 23 def __next__(self): 24 if self.node: 25 cur_node = self.node 26 self.node = cur_node.next 27 return cur_node.item 28 else: 29 raise StopIteration 30 31 def __iter__(self): 32 return self 33 34 def __init__(self,iterable = None): 35 self.head = None 36 self.tail = None 37 if iterable: 38 self.extend(iterable) 39 40 def extend(self,iterable): 41 for obj in iterable: 42 self.append(obj) 43 44 def append(self,obj): 45 """ 46 使用尾插法,进行插入 47 :param obj: 48 :return: 49 """ 50 s = LinkList.Node(obj) # 链表节点创建 51 if not self.head: 52 self.head = s 53 self.tail = s 54 else: 55 self.tail.next = s 56 self.tail = s 57 58 def find(self,obj): 59 for val in self: 60 if val == obj: 61 return True 62 else: 63 return False 64 65 def __iter__(self): 66 return self.LinkListIterator(self.head) 67 68 def __repr__(self): 69 return "<<"+",".join(map(str,self)) +">>" 70 71 72 class HashTable(object): 73 """ 74 实现集合的部分功能,不可重复,可查询 75 """ 76 def __init__(self,size=101): 77 self.size = size 78 self.T = [LinkList() for _ in range(self.size)] # 创建寻址表 79 80 def h_func(self,k): 81 """ 82 哈希函数 83 :param k: 84 :return: 85 """ 86 return k%self.size 87 88 def find(self,k): 89 """ 90 根据给定的k值在现有的范围中查找是否存在 91 :param k: 92 :return: 93 """ 94 hash_num = self.h_func(k) # 获取给定数值的hash值 95 return self.T[hash_num].find(k) 96 97 98 def insert(self,k): 99 """ 100 实现插入前去重 101 :param k: 102 :return: 103 """ 104 if self.find(k): 105 print('element is exist') 106 else: 107 hash_num = self.h_func(k) # 获取插入的值的hash值 108 self.T[hash_num].append(k) 109 110 111 my_set = HashTable() 112 my_set.insert(1) 113 my_set.insert(2) 114 my_set.insert(102) 115 print(my_set.T) 116 print(my_set.find(2))
-
-
Python中hash的使用,通过调用hashlib模块实现
-
通过hashlib调用不同的hash函数,实现不同数据的不同处理。
-
实例化hash对象,hash_obj = hash.hash函数类型() ,实例化过程中,可以通过添加参数,实现加盐操作
-
常见的hash函数类型有md5,sha1,sha224,sha256,sha384,sha512等
- hash_obj.update( 处理内容 ) 注意,需要进行处理的内容必须是bytes类型
- hash_obj.digest() ,返回当前已处理内容的hash值(内容摘要),返回值二进制数据
- hash_obj.hexdigest(),返回当前已处理内容的hash值(内容摘要),返回值是十六进制数据
-
-
-
MD5
- 曾是密码学中常用的hash函数
- 主要特点:
- 同样的消息MD5相同
- 可以快速计算出任意长度的消息的MD5
- 除非暴力美剧,否则基本不能从哈希值反推出消息本身
- 两条消息之间,即使是只有微笑差别,其MD5应该是完全不同,不相关的
- 在有限时间内,无法人工构建出MD5值相同的两个不同的信息
- 应用举例:
- 验证文件,例如是否是相同的文件,上传下载文件的完整性、云盘秒传等
-
SHA-1,SHA-2
- SHA-1和MD5都是曾经在密码学上经常用到的hash算法,但是目前,较为常用的是SHA-2
- SHA-2算法包含,SHA-224,SHA-256,SHA-384,SHA-512,SHA-512/224,SHA-512/256等算法,穷224,256,384与512代表的是哈希值的长度
树结构
树是一种可以递归定义的数据结构
- 基本概念
- 根节点,叶子节点
- 树的深度(高度),有根节点向下走的层数
- 树的度,每个节点上分叉的数量就是节点的度。所有节点中最大的度作为树的度
- 子节点、父节点:
- 子树
- 树的简单示例
- 模拟文件管理目录结构:
-
![]() View Code
View Code# !/usr/bin/python # -*- coding:utf-8 -*- """ 文件管理目录结构 """ import re class Node(object): """ 目录树结构中的节点类,模拟节点, """ def __init__(self,name,type='dir'): """ 节点信息,默认为文件路径,需要时将type设为文件 :param name: :param type: """ self.name = name self.type = type self.children = [] # 存储当前路径下的子节点 self.parent = None # 存储父级节点 def __repr__(self): return self.name class FileSysTree(object): """ 文件管理目录结构类 """ def __init__(self): self.root = Node('/') # 维护一个根“/” self.cur_dir = self.root # 将根节点设置成当前的默认目录 def mkdir(self,name): """ 单个文件路径创建 :param name: 文件路径名称 :return: """ if name[-1] != '/': name+='/' # 如果给定的文件路径,不是以“/”结尾的,进行补全 new_dir = Node(name) self.cur_dir.children.append(new_dir) new_dir.parent = self.cur_dir def ls(self): """ 返回当前目录中的子路径或子文件 :param name: :return: """ return self.cur_dir.children def cd(self,name): if name[-1] != '/':name+='/' for child in self.cur_dir.children: if name == '../': if self.cur_dir.name != '/': self.cur_dir = self.cur_dir.parent else: print('当前是根目录') break elif child.name == name: self.cur_dir = child break else: raise ValueError('invalid dir') def action(tree): """ 对目录树的操作函数 :param tree: :return: """ while True: info = input('%s请输入指令>>>'%tree.cur_dir.name).strip() if re.match(r'cd .*?',info): info = info.lstrip('cd ') tree.cd(info) elif re.match(r'^ls$',info): print(tree.ls()) elif re.match(r'mkdir .*?',info): info = info.lstrip('mkdir ') tree.mkdir(info) if __name__ == '__main__': tree = FileSysTree() tree.mkdir('test1') tree.mkdir('test2/') tree.mkdir('bin/') action(tree)
-
- 模拟文件管理目录结构:
-
二叉树
- 度不超过二的树,
- 对于完全二叉树,可以很方便的通过列表的线性存储方式,此外,完全二叉树以及其他二叉树都可以通过链表的链式存储实现
- 链式存储形式搭建的二叉树在执行效率上相对较高
- 链式存储的二叉树的创建
- 可以用单链表(只向下记录子节点信息)也可以用双链表(存储了子节点和父节点的信息)
- 二叉树的遍历
- 分为前序遍历、中序遍历、后序遍历和层级遍历四种方式
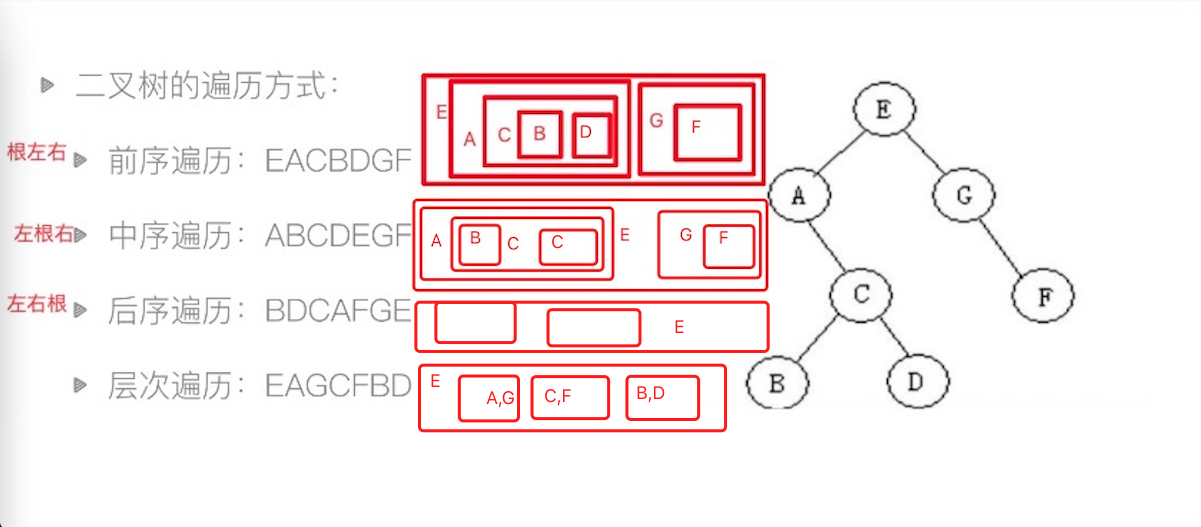
- 前序遍历,根在最前,每层的遍历顺序为,根左右
- 中序遍历,根在结果中间,每层遍历顺序为,左根右
- 后序遍历,根在结果最后,每层遍历顺序为,左右根
- 层级遍历,自根开始,每层进行逐一遍历
- 结合两种遍历打印的结果,就能反推出二叉树的原始形态
![]()
- 遍历的简单实现
-
![]() View Code
View Codefrom collections import deque class Node(object): def __init__(self,item): self.item = item self.lchild = None self.rchild = None self.parent = None def create_tree(): a=Node('A') b = Node('B') c = Node('C') d = Node('D') e = Node('E') f = Node('F') g = Node('G') e.lchild = a e.rchild = g a.rchild = c g.rchild = f c.lchild = b c.rchild = d return e def pre_check(root): """ 遍历打印顺序,中左右 :param root: :return: """ if root: print(root.item,end=',') pre_check(root.lchild) pre_check(root.rchild) def in_check(root): """ 遍历打印顺序,左中右 :param root: :return: """ if root: in_check(root.lchild) print(root.item,end=',') in_check(root.rchild) def post_check(root): """ 遍历打印顺序,左右中 :param root: :return: """ if root: post_check(root.lchild) post_check(root.rchild) print(root.item,end = ',') def level_check(root): """ 借助于队列实现层级管理 :param root: :return: """ queue = deque() queue.append(root) while len(queue): cur_node = queue.popleft() print(cur_node.item,end=',') if cur_node.lchild: queue.append(cur_node.lchild) if cur_node.rchild: queue.append(cur_node.rchild) root = create_tree() print('\n','前序遍历') pre_check(root) print('\n','中序遍历') in_check(root) print('\n','后序遍历') post_check(root) print('\n','层次遍历') level_check(root)
- 分为前序遍历、中序遍历、后序遍历和层级遍历四种方式
- 二叉搜索树
- 二叉搜索树是一个二叉树,并且满足下面性质,
- x是二叉树的一个节点,如果y1,y2分别是左右子树的任一子节点,那么有 y1.key <= x.key <= y2.key
- 二叉搜索树的基本操作 :
- 二叉搜索树基本操作包含遍历,插入,删除,查找等
- 遍历,分为前序、中序、后序、层级
- 插入
- 查找
- 删除
-
![]() View Code
View Codeimport random class Node(object): def __init__(self,item): self.item = item self.lchild = None self.rchild = None self.parent = None class Bst(object): def __init__(self,li=[]): self.root = None for ele in li: self.insert2(ele) def insert(self,item,cur_node=None): """ 递归实现的形式,二叉搜索树节点插入的函数, :param item: :param cur_node: :return: """ if not cur_node: cur_node = Node(item) else: if item < cur_node.item: # 当给定的值比当前节点的值小,则递归查看是否比左子节点小 cur_node.lchild = self.insert(item,cur_node.lchild) cur_node.lchild.parent = cur_node elif item >= cur_node.item: # 大多数情况下,二叉搜索树的节点值没有等值情况,当出现等值情况是,可以统一分配到左子树或左子树 cur_node.rchild = self.insert(item,cur_node.rchild) cur_node.rchild.parent = cur_node return cur_node def insert2(self,item): """ 循环实现方式, :param item: :return: """ p = self.root if not p: self.root = Node(item) else: while True: if item < p.item: if p.lchild: p = p.lchild else: p.lchild = Node(item) p.lchild.parent = p break elif item >= p.item: if p.rchild: p = p.rchild else: p.rchild = Node(item) p.rchild.parent = p break return def query(self,cur_node,item): """ 递归形式,查询 :param item: :return: """ if not cur_node: return None else: if item<cur_node.item: return self.query(cur_node.lchild,item) elif item>cur_node.item: return self.query(cur_node.rchild,item) else: return cur_node def query2(self,item): """ 循环形式,实现查询 :param item: :return: """ p = self.root while p: if item < p.item: p = p.lchild elif item>p.item: p = p.rchild else: return p return None def _remove0(self,node): """ 当要删除的节点是叶子节点时 :param node: :return: """ if not node.parent: # 如果当前的节点是树的根节点时,特殊处理,置空即可 self.root = None elif node == node.parent.lchild: node.parent.lchild = None elif node == node.parent.rchild: node.parent.rchild = None def _remove1l(self,node): """ 要删除的子节点只有一个左子节点时 :param node: :return: """ if not node.parent: self.root = node.lchild node.lchild.parent = None elif node == node.parent.lchild: node.parent.lchild = node.lchild node.lchild.parent = node.parent elif node == node.parent.rchild: node.parent.rchild = node.lchild node.lchild.parent = node.parent def _remove1r(self,node): """ 要删除的节点只有一个右子节点时 :param node: :return: """ if not node.parent: self.root = node.rchild node.rchild.parent = None elif node == node.parent.lchild: node.parent.lchild = node.rchild node.rchild.parent = node.parent elif node == node.parent.rchild: node.parent.rchild = node.rchild node.rchild.parent = node.parent def delete(self,val): """ 删除节点的操作函数 :param val: :return: """ if not self.root: return False else: cur_node = self.query2(val) if not cur_node: return False elif not cur_node.lchild and not cur_node.rchild: self._remove0(cur_node) elif not cur_node.rchild: self._remove1l(cur_node) elif not cur_node.lchild: self._remove1r(cur_node) else: # 当要删除的节点,左右子树都有的时候,处理方式有两种,选左子树中的最大值拿过来,替换掉删除的节点或者,拿右子树中的最小值替换掉删除的节点 # #========方式一,左子树中的最大值替换=========== max_node = cur_node.lchild while max_node.rchild: max_node = max_node.rchild cur_node.item = max_node.item if max_node.lchild: self._remove1l(max_node) else: self._remove0(max_node) # #==========方式二,右子树中的最小值替换=============== min_node = cur_node.rchild while min_node.lchild: min_node = min_node.lchild cur_node.item = min_node.item if min_node.rchild: self._remove1r(min_node) else: self._remove0(min_node) def pre_order(self,root): """ 前序遍历 :param root: :return: """ if root: print(root.item,end=',') self.pre_order(root.lchild) self.pre_order(root.rchild) def in_order(self,root): """ 中序遍历 :param root: :return: """ if root: self.in_order(root.lchild) print(root.item,end=',') self.in_order(root.rchild) def post_order(self,root): """ 后序遍历 :param root: :return: """ if root: self.post_order(root.lchild) self.post_order(root.rchild) print(root.item,end=',') test_list = [random.randint(1,10) for _ in range(10)] random.shuffle(test_list) my_tree = Bst(test_list) my_tree.pre_order(my_tree.root) print('') my_tree.in_order(my_tree.root) print('') my_tree.post_order(my_tree.root) print('') my_tree.delete(1) my_tree.in_order(my_tree.root) print('') my_tree.delete(5) my_tree.in_order(my_tree.root) print('') print('') check_node = my_tree.query(my_tree.root,5) check_node2 = my_tree.query2(2) print(check_node,check_node2)
- 二叉搜索树是一个二叉树,并且满足下面性质,
-
AVL树
-
自平衡的二叉搜索树,任何一个节点的子树高度差的绝对值不大于1
-
当AVL树的平衡因为插入节点或者删除节点导致原来平衡打乱,可以通过旋转来进行修正
-
(左左)右:当不平衡是对左子节点的左子树进行插入导致的,则通过右旋调整
-
(右右)左:当不平衡是对右子节点上的右子树进行插入导致的,则通过左旋调整
-
(左右)左右:对左子节点的右子树进行插入导致的不平衡,通过先左旋再右旋调整
-
(右左)右左:对右子节点上的左子树插入导致的不平衡,通过先右旋再左旋调整
-
-
![]() View Code
View Code""" 二叉树与AVL树 """ import random class Node(object): def __init__(self,item): self.item = item self.parent = None # 记录父级节点 self.lchild = None self.rchild = None self.bf = 0 # 平衡因子,设定左子树沉则为1,右子树沉则为2,左右子树高度相同则为0 class AVLTree(object): """ 先构建平衡操作,左右等旋转操作,再进行插入,每步插入动作之后及时做平衡调整 """ def __init__(self,li=[]): self.root = None if len(li): for ele in li: self.insert0(ele) def rotate_left(self,p,c): """ 右子树中的右子节点沉,则左旋。即右右左 :param p: :param c: :return: """ c.parent = p.parent if p.parent: if p.parent.lchild == p: p.parent.lchild = c else: p.parent.rchild = c p.rchild = c.lchild if c.lchild: c.lchild.parent = p c.lchild = p p.parent = c p.bf = 0 c.bf = 0 return c def rotate_right(self,p,c): """ 左子树的左子节点沉,则向右旋转。左左右 :param p: :param c: :return: """ c.parent = p.parent if p.parent: if p.parent.lchild == p: p.parent.lchild = c else: p.parent.rchild = c c.parent = p.parent p.lchild = c.rchild if c.rchild: c.rchild.parent = p c.rchild = p p.parent = c c.bf = 0 p.bf = 0 return c def rotate_left_right(self,p,c): """ 先左旋再右旋 :param p: :param c: :return: """ g = c.rchild g.parent = c.parent c.rchild = g.lchild if g.lchild: g.lchild.parent = c c.parent = g g.lchild = c g.parent = p.parent if p.parent: if p.parent.lchild == p: p.parent.lchild = g else: p.parent.rchild = g p.lchild = g.rchild if g.rchild: g.rchild.parent = p p.parent = g g.rchild = p if g.bf == 1: c.bf = 0 p.bf = 1 elif g.bf == -1: c.bf = -1 p.bf = 0 else: # 当出入的是g本身的时候 c.bf =0 p.bf =0 g.bf=0 return g def rotate_right_left(self,p,c): """ 先右旋后左旋的操作 :param p: :param c: :return: """ g = c.lchild g.parent = c.parent c.lchild = g.rchild if g.rchild: g.rchild.parent = c g.rchild = c c.parent = g g.parent = p.parent if p.parent: if p.parent.lchild == p: p.parent.lchild = g else: p.parent.rchild = g p.rchild = g.lchild if g.lchild: g.lchild.parent = p g.lchild = p p.parent = g if g.bf == 1: # 当向g的右节点插入值导致不平衡时 p.bf = -1 c.bf = 0 elif g.bf ==-1: # 当想g的左节点插入值导致不平衡时 p.bf = 0 c.bf = 1 else: # 当插入的是g节点本身时,g.bf == 0 p.bf = 0 c.bf = 0 g.bf =0 return g def insert0(self,item): # # ============执行插入================ p = self.root if not p: self.root = Node(item) else: while True: if p.item > item: if p.lchild: p = p.lchild else: p.lchild = Node(item) p.lchild.parent = p new_node = p.lchild break elif p.item < item: if p.rchild: p = p.rchild else: p.rchild = Node(item) p.rchild.parent = p new_node = p.rchild break # #============更新bf================== while new_node.parent: # print('开始调整%s'%new_node.item) # print('父节点%s'%new_node.parent.item) if new_node.parent.lchild == new_node: # 插入的位置是一个左子树,更新后的节点的父节点的左子树的bf需要-1,根据父节点原bf值进行讨论 if new_node.parent.bf < 0: # 之前的时候-1,再插入操作完成后,应该成为了-2 if new_node.bf<0: # 判断是再左右哪个子节点进行的插入 new_node = self.rotate_right(new_node.parent,new_node) break else: new_node = self.rotate_left_right(new_node.parent,new_node) break elif new_node.parent.bf>0: # 插入前右子树大于左子树,在左子树上插入后bf为0了,而此时父级节点的高度没有变化,不再循环 new_node.parent.bf =0 break else: # 当插入节点的父节点bf之前是0,再插入左侧节点后,高度差变成了-1,是否影响到了再上一级节点,需要进一步循环判断 new_node.parent.bf = -1 new_node = new_node.parent # 向上一级,继续进行bf平衡判断 continue else: # 插入的位置是一个右子树,更新后节点父级节点的bf值+1 if new_node.parent.bf > 0: # 原来是大于0,也就是平衡状态的1,在更新完后成为了2 if new_node.bf>0: # 在右节点上的右子树上进行的插入造成的不平衡,进行左旋调整 new_node = self.rotate_left(new_node.parent,new_node) break else: # 在左子树上的右节点进行的插入, new_node = self.rotate_right_left(new_node.parent,new_node) break elif new_node.parent.bf <0: new_node.parent.bf = 0 break else: new_node.parent.bf = 1 new_node = new_node.parent continue if not new_node.parent: self.root = new_node def pre_order(self,node): if node: print(node.item,end=',') self.pre_order(node.lchild) self.pre_order(node.rchild) def in_order(self,node): if node: self.in_order(node.lchild) print(node.item,end=',') self.in_order(node.rchild) def post_order(self,node): if node: self.post_order(node.lchild) self.post_order(node.rchild) print(node.item,end=',') # test_list = list(set(random.randint(1,100) for _ in range(10))) # print(test_list) # tree = AVLTree(test_list) tree = AVLTree([9,8,7,6,5,4,3,2,1]) # tree.pre_order(tree.root) # print('------------------') tree.pre_order(tree.root) print() tree.in_order(tree.root) # print('--------------->',tree.root.item)
-
-
B树,是对AVL树的扩展,是一个多叉(多路)自平衡的搜索树。常见的应用场景是数据库的索引。
-
B+树,是对B树的再次升级扩展