多边形平滑算法-ChaikinSmoothing
1 import math 2 3 # visualisation 4 import matplotlib.pyplot as plt 5 import matplotlib.lines as lines 6 # visualisation 7 8 def Sum_points(P1, P2): 9 x1, y1 = P1 10 x2, y2 = P2 11 return x1+x2, y1+y2 12 13 def Multiply_point(multiplier, P): 14 x, y = P 15 return float(x)*float(multiplier), float(y)*float(multiplier) 16 17 def Check_if_object_is_polygon(Cartesian_coords_list): 18 if Cartesian_coords_list[0] == Cartesian_coords_list[len(Cartesian_coords_list)-1]: 19 return True 20 else: 21 return False 22 23 class Object(): 24 25 def __init__(self, Cartesian_coords_list): 26 self.Cartesian_coords_list = Cartesian_coords_list 27 28 def Find_Q_point_position(self, P1, P2): 29 Summand1 = Multiply_point(float(3)/float(4), P1) 30 Summand2 = Multiply_point(float(1)/float(4), P2) 31 Q = Sum_points(Summand1, Summand2) 32 return Q 33 34 def Find_R_point_position(self, P1, P2): 35 Summand1 = Multiply_point(float(1)/float(4), P1) 36 Summand2 = Multiply_point(float(3)/float(4), P2) 37 R = Sum_points(Summand1, Summand2) 38 return R 39 40 def Smooth_by_Chaikin(self, number_of_refinements): 41 refinement = 1 42 copy_first_coord = Check_if_object_is_polygon(self.Cartesian_coords_list) 43 while refinement <= number_of_refinements: 44 self.New_cartesian_coords_list = [] 45 46 for num, tuple in enumerate(self.Cartesian_coords_list): 47 if num+1 == len(self.Cartesian_coords_list): 48 pass 49 else: 50 P1, P2 = (tuple, self.Cartesian_coords_list[num+1]) 51 Q = obj.Find_Q_point_position(P1, P2) 52 R = obj.Find_R_point_position(P1, P2) 53 self.New_cartesian_coords_list.append(Q) 54 self.New_cartesian_coords_list.append(R) 55 56 if copy_first_coord: 57 self.New_cartesian_coords_list.append(self.New_cartesian_coords_list[0]) 58 59 self.Cartesian_coords_list = self.New_cartesian_coords_list 60 refinement += 1 61 return self.Cartesian_coords_list 62 63 if __name__ == "__main__": 64 Cartesian_coords_list = [(1, 1), 65 (1, 3), 66 (4, 5), 67 (5, 1), 68 (2, 0.5), 69 (1, 1),] 70 71 obj = Object(Cartesian_coords_list) 72 Smoothed_obj = obj.Smooth_by_Chaikin(number_of_refinements=5) 73 74 # visualisation 75 x1 = [i for i, j in Smoothed_obj] 76 y1 = [j for i, j in Smoothed_obj] 77 x2 = [i for i, j in Cartesian_coords_list] 78 y2 = [j for i, j in Cartesian_coords_list] 79 plt.plot(range(7), range(7), 'w', alpha=0.7) 80 myline = lines.Line2D(x1, y1, color='r') 81 mynewline = lines.Line2D(x2, y2, color='b') 82 plt.gca().add_artist(myline) 83 plt.gca().add_artist(mynewline) 84 plt.show()
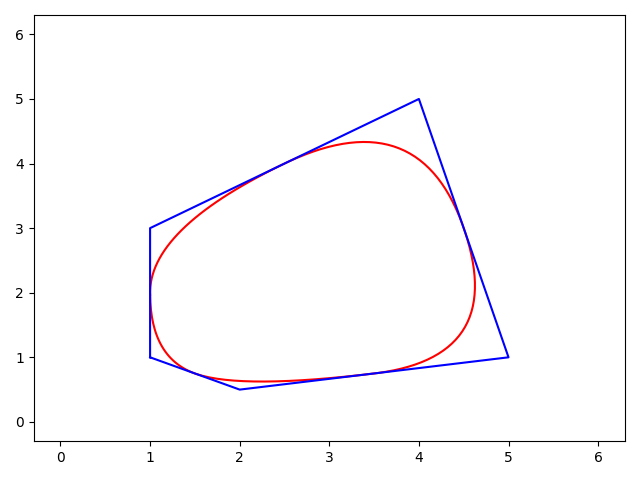
个人学习记录




