Task2-DatawhaleX 李宏毅苹果书AI夏令营-深度学习入门

Task2-DatawhaleX 李宏毅苹果书AI夏令营-深度学习入门

1.学习链接：

教程链接：

https://linklearner.com/activity/16/14/55

李宏毅老师对应视频课程：

哔哩哔哩1:

                          

哔哩哔哩2: 

                           

2.学习笔记整理：

文档内容梳理

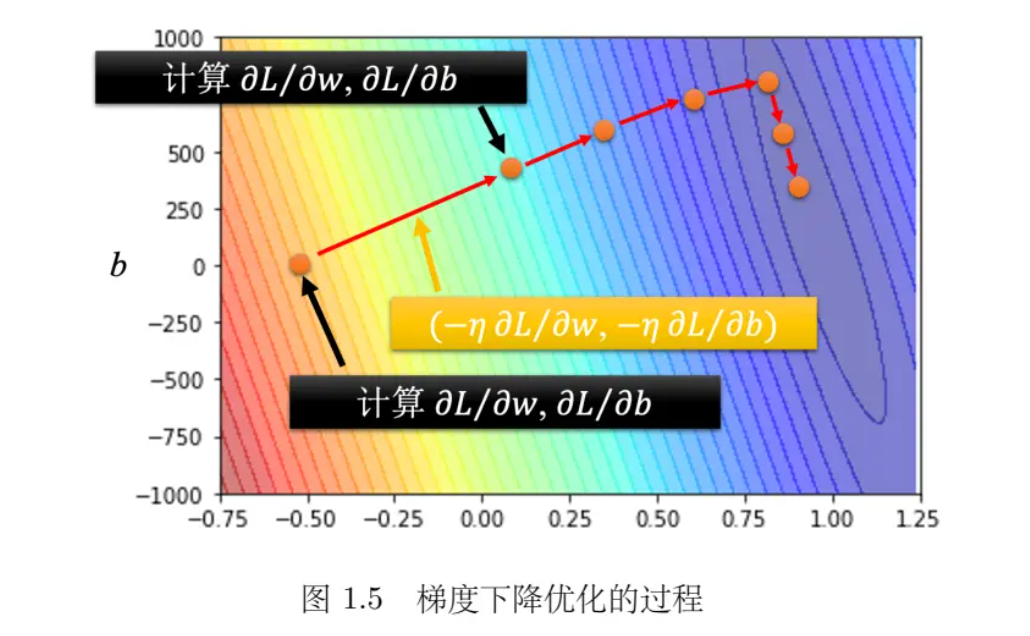
1. 梯度下降优化过程

  • 公式: 

    \begin{array}{l}
    w1=w 0-\left.\eta \frac{\partial L}{\partial w}\right|_{w=w 0, b=b 0} \\
    b1=b 0-\left.\eta \frac{\partial L}{\partial b}\right|_{w=w 0, b=b 0}
    \end{array}

    其中，\( \eta \) 是学习率，\( \frac{\partial L}{\partial w} \) 和 \( \frac{\partial L}{\partial b} \) 分别是损失函数L对 w 和 b 的偏导数。
  • 过程: 开始时选择初始值 \( w_0 \) 和 \( b_0 \)，通过计算损失函数 L 对 w 和 b 的偏导数来更新权重和偏置，以最小化损失。

                                     

2. 线性模型及其局限性

  • 基础线性模型: \( y = b + wx_1 \)
  • 局限性: 线性模型只能表示直线关系，无法模拟复杂的非线性关系。

                                             

3. 分段线性曲线与逼近连续曲线

  • 分段线性曲线: 由多个线性段组成，可以逼近任意连续曲线。
  • 逼近方法: 通过增加分段线性曲线的分段数，可以提高逼近的精度。

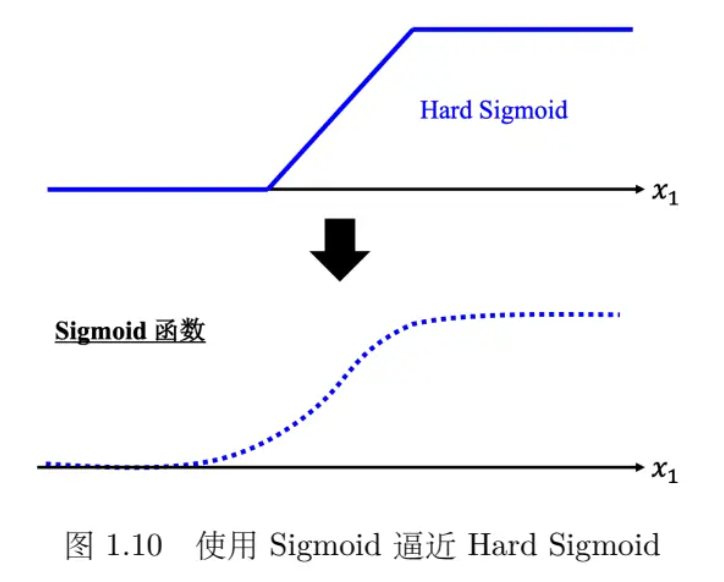
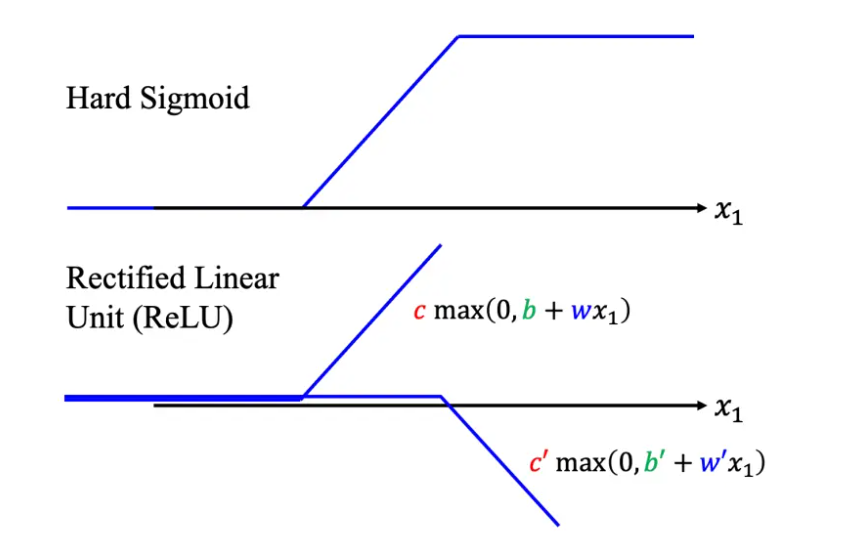
4. Sigmoid 函数与 Hard Sigmoid

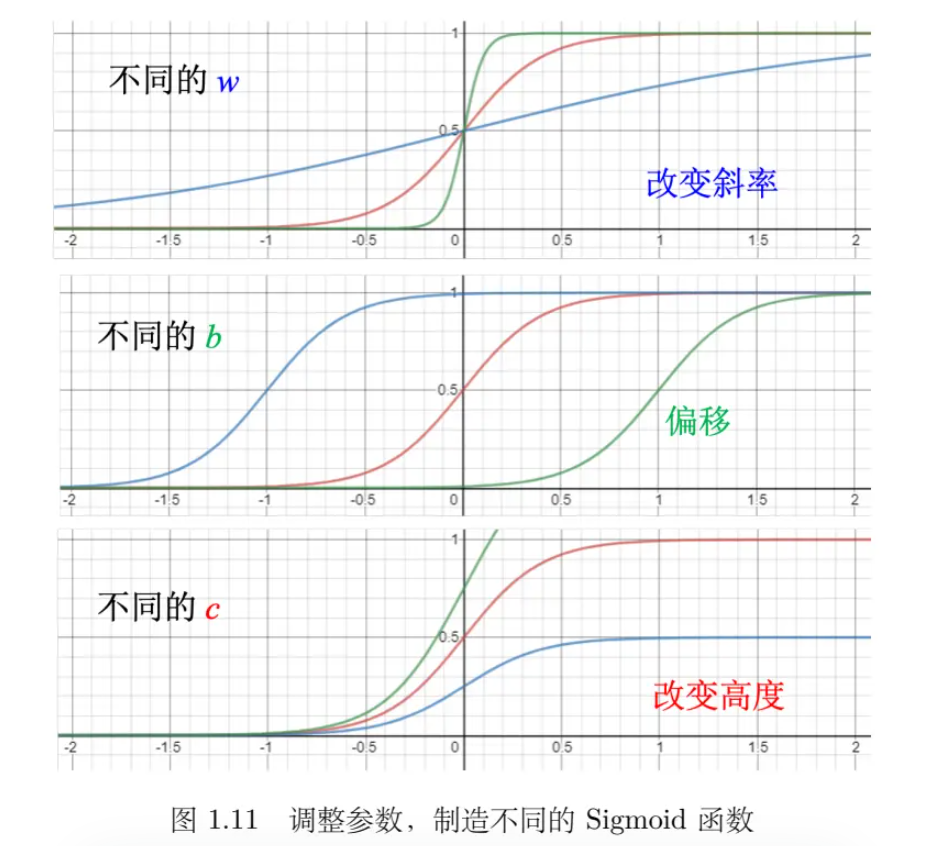
  • Sigmoid 函数: \( y = \frac{c}{1 + e^{-(b + wx_1)}} \)
  • Hard Sigmoid: 一种分段线性的 Sigmoid 函数，可以用多个 Sigmoid 函数逼近。

                                                             

                                                       

5. 神经网络模型构建

  • 模型表示: \( y = b + \sum c_i \sigma(b_i + w_{ij}x_j) \)
  • 参数: \( b \), \( w \), \( c \) 是模型的参数，\( x_j \) 代表特征，\( \sigma \) 为 Sigmoid 激活函数。

6. 模型优化与梯度下降

  • 损失函数: \( L(\theta) \) 用于评估参数 \( \theta \) 的好坏。
  • 梯度: \( g = \nabla L(\theta_0) \) 表示损失函数对参数的偏导数，用于指导参数更新。

7. 批量梯度下降

  • 批量处理: 将数据分为多个批量，每次使用一个批量的数据来计算损失和梯度，更新参数。

8. 模型变形与激活函数

  • ReLU 函数: \( c \cdot \max(0, b + wx_1) \) 一种常用的激活函数，可以构造更复杂的函数形式。
  • 激活函数作用: 增加模型的非线性能力，使其能够逼近更复杂的函数。

                                                           

 

                                                      

9. 神经网络的层与深度学习

  • 层: 多个神经元组成一层，多层堆叠形成深层网络。
  • 深度学习: 通过增加网络的深度，提高模型的学习能力和表达能力。

10. 过拟合问题

  • 现象: 在训练数据上表现很好，但在未见过的数据上表现差。
  • 原因: 模型过于复杂，对训练数据过度拟合。

11. 机器学习框架

  • 训练过程: 包括定义模型、损失函数和优化算法。
  • 测试: 使用训练好的模型在测试集上进行预测。

 

公式记录与分析见解：

  1. 权重和偏置更新: 梯度下降算法通过计算损失函数对权重和偏置的偏导数来更新它们，目的是减少预测误差。
  2. 分段线性曲线逼近: 分段线性曲线通过组合多个线性段来逼近复杂的连续曲线，这显示了通过组合简单模型可以解决复杂问题。
  3. Sigmoid 函数: Sigmoid 函数是一个非线性激活函数，它可以将输入压缩到 (0, c) 区间内，常用于神经网络中引入非线性。
  4. 损失函数: 损失函数 \( L(\theta) \) 用于量化模型预测与实际值之间的差异，优化目标是找到最小化损失函数的参数 \( \theta \)。
  5. 梯度计算: 梯度 \( \nabla L(\theta_0) \) 是损失函数对参数的偏导数向量，它指示了损失函数在参数空间中增长最快的方向。
  6. 批量梯度下降: 通过分批处理数据，可以减少计算资源的需求，同时保持梯度下降算法的有效性。
  7. ReLU 函数: ReLU 函数是一种常用的激活函数，它在正区间内保持线性，而在负区间内输出为零，有助于解决梯度消失问题。
  8. 多层神经网络: 通过堆叠多个隐藏层，神经网络可以学习更复杂的特征表示，这是深度学习的核心概念。
  9. 过拟合: 过拟合发生在模型在训练数据上表现很好，但不能泛化到新数据上，这是模型复杂度过高的结果。
  10. 机器学习框架: 描述了从定义模型、损失函数到优化算法的整个训练过程，以及如何使用训练好的模型进行预测。

 

3.分析总结：

Point1：批量梯度下降（Batch Gradient Descent）和随机梯度下降（Stochastic Gradient Descent, SGD）在实际应用中不同的特性和适用场景分析。

批量梯度下降（Batch Gradient Descent）

定义:批量梯度下降在每次更新参数时使用全部数据集来计算损失函数的梯度。这意味着每次迭代都会计算整个数据集上的损失函数，然后根据这个损失函数的平均梯度来更新模型的参数。

特点:
计算成本高: 
每次更新需要使用全部数据集，因此计算量大，尤其是在数据集很大的情况下。
收敛性: 
通常收敛到全局最小值，但收敛速度可能较慢。
内存需求: 
需要足够的内存来存储整个数据集。
稳定性: 
由于每次更新都是基于整个数据集，因此更新步长相对稳定。
适用场景:
当数据集不是特别大，可以一次性加载到内存中时。
当模型的参数更新需要非常精确时。
在一些需要高准确度的领域，如金融风险评估。

随机梯度下降（Stochastic Gradient Descent）

定义：随机梯度下降在每次更新参数时只使用一个数据点（或一小批数据点）来计算损失函数的梯度。每次迭代只基于一个样本或小批量样本来更新模型参数。

特点:
计算成本低: 
每次更新只需要一个样本，因此计算量小，适合大数据集。
收敛速度: 
通常收敛速度快，但可能收敛到局部最小值而非全局最小值。
内存需求低: 
只需要加载少量数据，内存使用少。
更新频率高: 
参数更新频繁，可能导致训练过程中的噪声较大。
适用场景:
当数据集非常大，无法一次性加载到内存中时。
当需要快速训练模型时，尤其是在时间敏感的应用中。在一些可以容忍一定误差，但需要快速迭代的领域，如在线推荐系统。

小批量梯度下降（Mini-batch Gradient Descent）

定义： 介于批量梯度下降和随机梯度下降之间的是小批量梯度下降，它每次更新使用一小批数据点来计算梯度。

这种方法结合了两者的优点：
特点:
计算效率: 
比批量梯度下降高，因为不需要用到全部数据。
稳定性:
比随机梯度下降好，因为每次更新是基于多个样本的。
内存需求: 
适中，适合大多数现代计算机系统。
适用场景:
在数据集较大，但内存资源有限的情况下。
当需要平衡计算效率和模型性能时。
在深度学习和其他需要大量参数更新的领域中广泛使用。
其实在无论我们选择哪种梯度下降方法取决于具体问题的需求、数据集的大小、计算资源和内存限制。在实际应用中，小批量梯度下降因其平衡了计算效率和稳定性而成为最常用的方法。

Point2：防止模型过拟合的一些常用的策略：

数据增强（Data Augmentation）:
通过对训练数据进行变换（如旋转、缩放、裁剪等）来增加数据的多样性，从而提高模型的泛化能力。
正则化（Regularization）:
L1 正则化（Lasso 正则化）和 L2 正则化（Ridge 正则化）是常见的方法，它们通过在损失函数中添加一个正则项来惩罚模型的复杂度。
Dropout:
在训练过程中随机丢弃（置零）一部分神经元的输出，这可以防止网络对训练数据中的特定样本过度敏感。
提前停止（Early Stopping）:
在训练过程中监控验证集上的性能，当验证集上的性能不再提升或开始下降时停止训练。
交叉验证（Cross-validation）:
使用多个训练/验证数据集组合来评估模型性能，确保模型在不同的数据子集上都能表现良好。
集成学习（Ensemble Learning）:
训练多个模型并将其结果结合起来，以减少单个模型的过拟合风险。
减少模型复杂度:
减少模型的大小，例如减少网络层数或每层的神经元数量。
使用更多的训练数据:
如果可能的话，增加训练数据的数量可以帮助模型学习到更泛化的特征。
添加噪声:
在训练过程中向输入数据或权重中添加噪声，以提高模型对输入变化的鲁棒性。
特征选择（Feature Selection）:
选择与任务最相关的特征，去除无关或冗余的特征。
调整超参数:
通过调整学习率、批量大小等超参数，找到合适的训练配置。

 Point3:  为什么需要引入激活函数：

以下是激活函数的一些关键作用：
增加模型的灵活性: 通过使用激活函数，如 Sigmoid 或 ReLU，可以创建更复杂的分段线性曲线，这些曲线可以逼近更复杂的连续函数。
模拟复杂关系: 线性模型可能过于简单，无法捕捉数据中的复杂关系。激活函数可以引入非线性，使得模型能够学习和模拟更复杂的数据模式。
构建深层网络: 在深度学习中，多个激活函数（神经元）可以堆叠成多层网络，每一层都能够学习数据的不同特征表示。
常用的激活函数：
Sigmoid 函数: 用于逼近 Hard Sigmoid 函数，具有 S 型曲线，可以将输入压缩到 (0, 1) 或其他范围内。
Hard Sigmoid 函数: 一种分段线性的激活函数，可以用多个 Sigmoid 函数来逼近。
ReLU 函数: 修正线性单元，当输入大于零时输出输入值，否则输出零，有助于解决梯度消失问题，并增加网络的非线性。
如何使用激活函数来增加模型的复杂度？
多个 Sigmoid 函数: 通过调整不同的参数 𝑏,𝑤,𝑐 可以创建不同的 Sigmoid 函数，并将它们相加来逼近分段线性曲线。
使用 ReLU 函数: 通过堆叠多个 ReLU 层，可以创建更深的神经网络，从而增加模型的复杂度和学习能力。
模型变形：
分段线性曲线: 通过组合多个 Hard Sigmoid 函数来逼近分段线性曲线。
使用多个特征: 将多个特征组合起来，形成更复杂的模型。增加网络深度: 
通过增加隐藏层的数量来增加模型的深度，从而提高模型的学习能力。
这些模型变形和激活函数的使用都是为了提高模型的表达能力和泛化能力，使其能够更好地适应和预测复杂的数据模式。

 

posted @ 2024-08-30 12:17  谁的青春不迷糊  阅读(23)  评论(0)  编辑  收藏  举报