旧试题

复习计划

旧试题

多回顾以前会的算法来形成自己的体系. ---zzs

较熟练:

6.19 SAM
6.17 SA
基础李超树
splay
Min-Max 容斥
分治NTT

数据结构(图)
6.17 左偏树
6.14 K-D TreeP3769 [CH弱省胡策R2]TATT
6.10 动态点分, 边分(三度化)BZOJ2870.最长道路tree
6.15 笛卡尔树
6.15 斯坦纳树
6.14 (混合图)欧拉回路

LCT(维护子树信息)P4546 [THUWC2017]在美妙的数学王国中畅游
长链剖分(k级祖先)[POI2014]HOT-Hotels 加强版
点双,边双,双强联通分量相关
prufer 序列(运用,转化)
二分图最大权匹配-KM算法

数学
6.13 (ex)CRT
6.15 线性基(第k大, 离线删除)总结
6.14 任意模数NTT
6.15 杜教筛, 线性筛法总结
6.15 (线性)高斯消元[BJOI2018]治疗之雨可能还要看看的题解
6.16 Miller-Robin
6.18 容斥UOJ390.【UNR #3】百鸽笼
6.18 反演(子集反演, strling反演, Mobius反演, 最值反演, 单位根反演)总结
6.18 数论相关(狄利克雷卷积, 数论函数及其性质)
6.19 Burnside(Polya)
6.19 原根相关
6.19 多项式相关 (求逆, 求ln)
6.19 (ex)BSGS

(ex)LUCAS
strling数(CF961G), 组合数, Bell数, Catalan数的trick
Pollard-Rho
"十二重计数法"

其他
6.15 差分约束
6.17 带修莫队, 树上莫队, 回滚莫队
6.19 半平面交
6.19 旋转卡壳
6.19 CDQ分治
6.19 整体二分

DP 优化 (单调性, 斜率, 四边形不等式)
网络流, 费用流模型
KMP, AC自动机的运用
回文自动机
Manacher
博弈论(SG, NIM..)总结

完全不会:

610 Segmenttree beats BZOJ4695.最假女选手
6.19 圆方树(仙人掌)

线性代数相关(常系数齐次线性递推, BM, C-H定理, 特征多项式相关, 矩阵树定理)
可持久化平衡树
插头DP
树套树
wqs二分
Min_25 筛
多项式相关 (exp, 开根, 快速差值, 求值)
带花树算法
二次剩余

考试总结(复习)

6月

test20200616旅行(AGC023D): 正难则反! 在时间上从后往前考虑会很简单
test20200613干扰: \(n\) 个点的凸包, 任取三个相邻的点构成的圆, 这些圆中最大的那个一定包含了所有的 \(n\) 个点.
test20200612Three: 每个区间的贡献是前三大的数的积, 算所有区间的贡献和: 将每个区间的贡献在最小的数处算, 然后从大往小插入数字.
test20200611行走: 相同个起点终点, 求不相交的路径总数: 容斥->行列式(LGV定理).
test20200611蚯蚓: 如果有加点, 删点操作, 可以考虑 trie 树; 每次暴力重构 trie 的时间复杂度是对的.
test20200609数列: 给定一个数列然后一个数一路模过去的题, 考虑最小的数放在哪, 然后相当于可以随便选; 考虑将所有数从大到小排序然后依次确定每个位置填啥数, 某些数如果当时不填后面就没用了.
test20200608matrix: 贡献分开考虑(计算), 如果一起考虑的话可能并不是很好算, 但是确定了左右端点之后贡献就只需要管完全相同的部分即可.
test20200606sequence: 正确识别考场上给出的 NPC 问题, 不要做徒劳的思考.
test20200606仙人掌: 学会考虑计数的意义, 不要无从下手.
test20200605要换换名字: 正确观察性质
test20200605获取名额: 学会用数学工具解决问题, 对于连乘的形式, 可以把它去对数变成连加的形式.
test20200605动态半平面角: 牢记区间 LCM 的拆贡献算法, 在树上用 LCA 搞搞即可.
test20200603排序: 排列问题, 直接设状态高斯消元搞不得, 于是想到用轮换去计数, 这样划分数就挺小了.
test20200603机器人: 树上联通块问题, 每次覆盖一条路径, 有多少个联通快等价于有多少个点到父亲的边没有被覆盖.
test20200601染色问题: 同样是 NP-Hard 问题, 那么只能通过缩小问题规模解决. 由于保证了m-n<=5, 那么把所有二度点和三度点都缩掉, 可以将数据范围降智 n<=10 且 m<=15. 缩边的时候对于每条边记录一下这条边两端颜色相同/不同时的方案数.

5月

test20200529盗梦空间: 考场上适当分析难度, 认为最简单的题不一定真的是最简单的题; 虚树, 有多个点的时候可以考虑求出每个点的管辖范围.
test20200526骨牌: 注意区分 插头 和 轮廓线 的区别. 这道题用插头可能会很麻烦.
test20200525梦批糼: 三维问题考虑降维; 矩形面积的差分算法.
test20200525等你哈苏德: 注意可以用到网络流模型; 混合图网络流的解法.
test20200521图: 经典染色计数原理, 对于一个点如果和它颜色不同的点的颜色互不相同则可直接乘法原理.
test20200518s3mple: 转移时用到多项式卷积的, 可以考虑转成点集运算在转回来 应该是一个烂大街的技巧了.
test20200518s1mple: 状态数太多可以考虑合并相同的状态(枚举划分之类的...)
test20200516栈: 直接做不好做考虑转化顺序, 比如扫描时间线之类的.
五一集训

通过导数算两次的方法来求一个多项式的 \(n\) 次幂.
学会分类讨论, 通过不变量计数.
线性基的 \(O(\log)\) 离线删除操作(拟阵, 类似最大生成树), 以及在线删除操作.
适当的根号分治优化, 在涉及 GCD 的问题上考虑质因子及其次幂的贡献, 学会按照套路将式子化成好维护的形式.
学会往费用流方面想, 并看能不能模拟.
用 FFT 处理关于通配符的字符串匹配问题.
计数(概率,期望)问题每个元素分开考虑
涉及 DP 优化时, 如果要求单调性看能不能将 DP 值取个前缀 max.
要理解一些排序的原理.
莫队算法注意如果询问和修改次数不一样要平衡.
考场上大胆猜想+打表.
学会适当的放松一些条件来计数.
涉及到在自动机上走的问题(DP), 看能不能倍增或者轻重链优化.
计数但是不用模数输出的题, 往往精度不要求做到完美.

数学

组合数拆成多项式

贡献是组合数的时候考虑将其拆成多项式来维护.(如果底数比较小的话)(下降幂多项式)

广义二项式定理

牛顿二项式系数 \({r \choose n}\), 设 \(r\) 为实数, \(n\) 为整数:

\[{r \choose n}= \begin{cases} 0， & n<0\\ 1， & n=0\\ \frac{r(r-1)\cdots (r-n+1)}{n!}， & n>0 \end{cases} \]

广义牛顿二项式定理:

\[(x+y)^{\alpha}=\sum_{n=0}^\infty{\alpha \choose n}x^{n}y^{\alpha-n} \]

其中 \(x，y，α\) 为实数，且 \(\mid\frac{x}{y}\mid<1\).

数论函数常见等式

\(\phi*I=id\)
\(\mu *I=e\)
\(\mu *id=\phi\)

邻接矩阵行列式的计算

考虑其"几何意义", 相当于把所有排列的贡献求和. 注意到一个排列有贡献当且仅当全是 1. 那么原图中点 i, p[i] 就必须有边. 这样下来原图相当于被分成了若干个环(或者匹配). 考虑算逆序对数, 由于一个连通块可以通过交换 sz-1 次变为升序, 而交换一次必然会改变逆序对的奇偶性, 所以这个排列的贡献就是 \((-1)^{\sum (sz_i-1)}=(-1)^{n-cnt}\), 其中 \(cnt\) 为联通块数.
test20200606仙人掌.

常见泰勒展开公式

在 \(x_0\) 处展开:

\[f(x)=\sum_{i=0}^{\infty}\frac{f^{(i)}(x_0)\cdot (x-x_0)}{i!} \]

对于精度误差要求在 \(10^{-8}\) 左右的题目一般取前 15-22 项来算即可.
「THUWC 2017」在美妙的数学王国中畅游:展开后用 LCT 维护.

test20200605获取名额:直接维护可能会爆精度, 需要根据 \(x\) 的大小分类讨论一下.

自然数幂和的处理问题

\[\sum_{i=1}^{n}{i^k} \]

设 \(f(n)\) 为这个值, 可以证明 \(f(n)\) 是一个 \(k\) 次多项式. 于是求出前 \(k+1\) 项的和作为点值插值即可.

区间 LCM 问题

问题描述: \(n\) 个数 \(a_i\), \(Q\) 次询问区间 \([l,r]\) 的 \(LCM\pmod {MOD}\), \(N,Q,a_i\leq 10^6\).
考虑将区间挂在询问右端点上, 然后从左到右扫数列, 将质数的贡献分发到它的每个幂次上去. 具体来说就是对于每个 \(p^k\) 记录它上次出现的位置, 然后加入一个数的因子 \(p^k\) 的时候就将 \(p\) 所有不大于 \(k\) 次幂的贡献搬到这个位置. (其实好像就相当于给每个质数维护一个单调栈, 然后差分一下?)
强制在线, 把树状数组换成主席树即可.
test20200605动态半平面交.

不相交路径计数

参考.
test20200611行走.

对任意划分的 \(\prod_{i=1}^{k} x_i\) (其中 \(\sum x_i\) 为定值 \(p\)) 求和的技巧:

反过去考虑插板法的组合意义,相当于插板完成后在每一组都任意选择一个代表球的方案数。那么列方程的时候变成两个变量,表示选的代表球之前的数目和之后的数目. \((X_1+Y_1)+(X_2+Y_2)+\dots+(X_k+Y_k)=p-k\). 类似的, \(\sum\prod\binom{x_i}{k_i}\) 也可以这么考虑.

子集反演

首先有一个结论:

\[\sum_{T\subseteq S}(-1)^{|T|}=[S=0] \]

于是乎

\[F[S]=\sum_{T\subseteq S}{G[T]}\Leftrightarrow G[S]=\sum_{T\subseteq S}{(-1)^{|S-T|}F[T]} \]

二项式反演

\[\sum_{i=0}^{n}{(-1)^i\binom{n}{i}}=[n=0] \]

参考, 参考:

\[f_n=\sum_{i=0}^{n}{\binom{n}{i}g_i}\Leftrightarrow g_n=\sum_{i=0}^{n}{(-1)^{n-i}\binom{n}{i}f_i} \]

min-max 容斥

\[\max(S) = \sum_{T\subseteq S, T \neq \varnothing} (-1)^{|T|-1}\min(T) \]

\[\max\ _{k}(S) = \sum_{T\subseteq S, |T| \geq k} (-1)^{|T|-k}\binom {|T|-1}{k-1} \min(T) \]

裴蜀定理拓展

方程

\[a_1x_1+a_2x_2+\dots+a_kx_k=y \]

有整数解的充要条件是 \(\gcd(a_1,a_2,\dots,a_k)|y\).

多项式相关

基础求导运算法则:

\((fg)'=f'g+fg'\)
\(\left( \frac{f}{g} \right)'=\frac{f'g-fg'}{g^2}(g\neq 0)\)

序列求前缀和相当于乘上 \(\frac{1}{1-x}=\sum_{i=0}^{+\infty}{x^i}\).

经典线性高斯消元

在树上时, 如果 \(f[u]\) 的值和与它相邻的节点有关, 可以设 \(f[u]=A_uf[fa[u]]+B_u\)(类似待定系数, 需要注意的是它要能够这样表示), 然后推式子发现 \(A_u,B_u\) 只和 \(u\) 的儿子有关, 于是可以从下往上递推. 例如「PKUWC2018」随机游走.
同理, 在序列上时, 若 \(f[i]\) 的值和 \(f[i+1],f[i-1]\) 有关, 可以根据具体性质, 设 \(f[i]=A_if[i-1]+B_i\), 然后想办法求出 \(A_i,B_i\) 的值. 例如「SHOI2017」分手是祝愿.

斐波那契 GCD

结论: \(\gcd(f[n],f[m])=f[\gcd(n,m)]\).

关于杨辉三角

test20200526二分图

用杨辉三角的前 \(n\) 行, 在每一行中选择一段连续的前缀, 使得前缀大小不降, 然后将选择的数加起来, 可以凑出 \([0,2^n-1]\) 中的所有数, 贪心从下往上构造即可.

多元二项式定理

\[(x_1+x_2+\dots +x_k)^p=\sum_{c_i\ge 0,\sum{c_i}=p}{\binom{p}{c_1,c_2,\dots,c_k}\cdot \prod_{i=1}^{m}{x_i^{c_i}}} \]

库默尔定理

设 \(n,m\) 为正整数, \(p\) 为素数，则 \(\binom{n+m}{m}\) 含 \(p\) 的幂次等于 \(m+n\) 在 \(p\) 进制下的进位次数.

排列相关

排列问题可以考虑按照置换, 将相同的归为一类来减少状态数.
test20200603排序.

图论

树直径

距离树上任意一个点最远的点一定是树直径的一个端点之一.
若干条树直径一定相交于中点(边).

树上联通块问题

(若干条连并成的)树上极大联通块, 可以考虑给每个联通块选择深度最浅的点作为关键点, 转化成求有多少个点被标记而其到父亲的边未被标记.
test20200603机器人.

平面图的欧拉定理

设 \(v,e,f,c\) 分别为平面图的点数, 边数(\(e\le 3v-6\)), 面数, 联通块数, 则 \(v-e+f=c+1\).

竞赛图的性质

例题.

字符串

关于回文串

以任意一个位置 \(r\) 结尾的所有回文子串 \(s[l_1..r],s[l_2..r],s[l_3..r],\dots,s[l_k..r]\) 的左端点按照从大到小排序后的序列 \(l_1,l_2,l_3,\dots,l_k\) 可以被划分成 \(O(\log n)\) 段, 使得每一段都是等差数列.

求区间本质不同的回文串个数就要用到这个引理.

字符串首尾添加, 删除字符的问题的 trick

可以考虑转化成 trie 树, 删除操作直接向父亲走.
AC 自动机上一个点 fail 树的子树中的所有点都是这个串的超串, 于是统计子树和即可.[NOI2011]阿狸的打字机.
如果首尾都有删除, 则可以维护两颗 "对顶" 的 trie 树. 若出现一颗 trie 被删完的情况, 暴力重建, 将根节点选在正中间即可. 可以势能分析出它的复杂度是 \(O(N)\) 的. test20200611蚯蚓.

杂项

swap 调用 STL 的复杂度问题:

𝑣𝑒𝑐𝑡𝑜𝑟,𝑚𝑎𝑝,𝑠𝑒𝑡,𝑑𝑒𝑞𝑢𝑒 调用复杂度：\(𝑂(1)\)
但是在开启 \(𝑐++11\) 的情况下这三种容器 𝑠𝑤𝑎𝑝 的复杂度可以做到 \(𝑂(1)\).
𝑝𝑟𝑖𝑜𝑟𝑖𝑡𝑦_𝑞𝑢𝑒𝑢𝑒,𝑞𝑢𝑒𝑢𝑒,𝑠𝑡𝑎𝑐𝑘 调用复杂度：\(𝑂(𝑛)\)
另外, 对两个数组进行 swap 的操作也是 \(O(n)\) 的，无论开不开 \(c++11\) 都一样
参考博客.

看上去很详细的OI知识汇总图

附: 常见泰勒展开公式
在 \(x_0\) 处展开:

\[f(x)=\sum_{i=0}^{\infty}\frac{f^{(i)}(x_0)\cdot (x-x_0)}{i!} \]

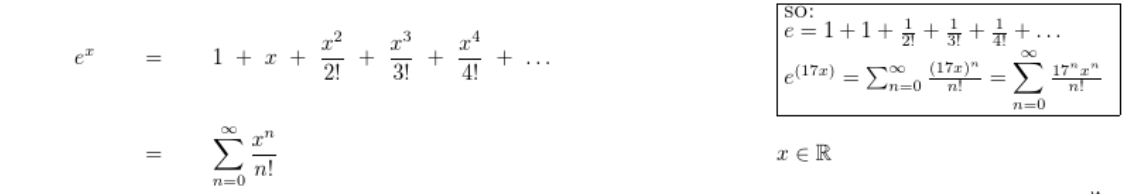
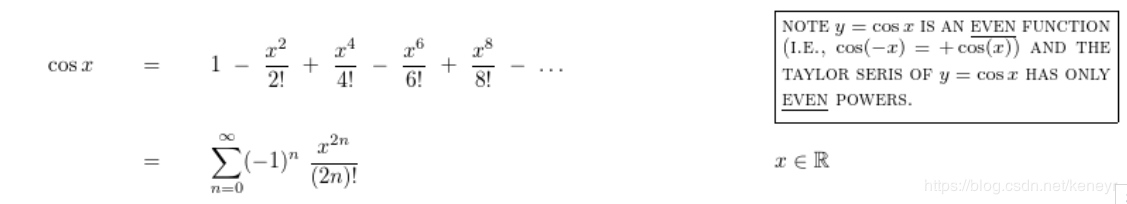
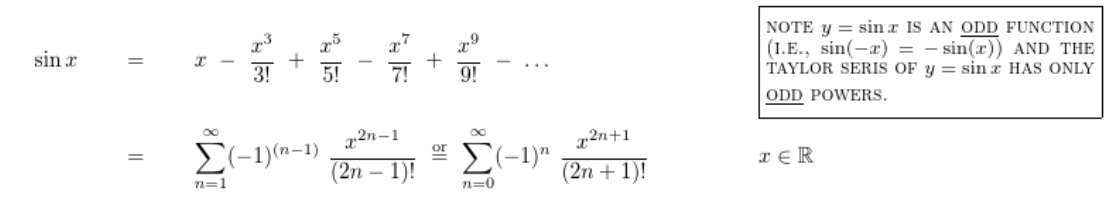
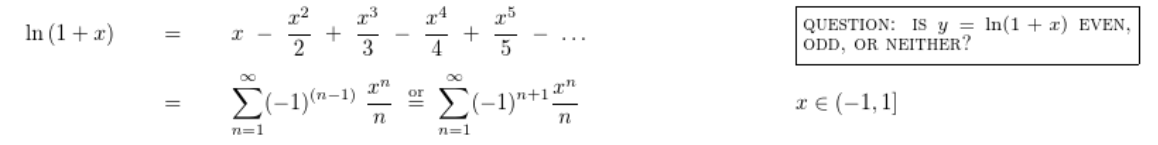
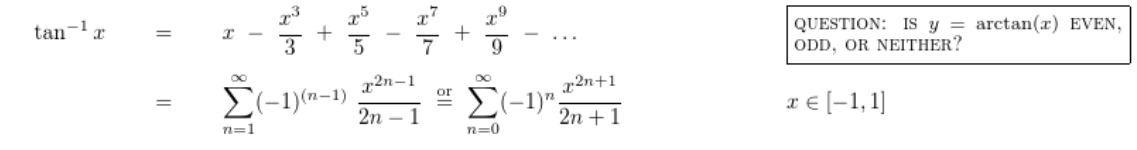
一些笔记

c++ 将函数名作为函数参数的具体操作

1.直接使用

int f(int a){rturn a+1;}
int use_f(int a,int (*func)(int)){return f(a);}

int main()
{
    int a;
    cin>>a;
    cout<<use_f(a,f)<<endl;
}

2.在结构体中使用
由于在结构体中直接如上的使用报错“非静态对象不能这样使用”，所以需要加上static

struct test
{
    static int f(int a){rturn a+1;}
    int use_f(int a,int (*func)(int)){return f(a);}
};
test T;

int main()
{
    int a;
    cin>>a;
    cout<<T.use_f(a,T.f)<<endl;
}

对于“删除某元素后剩余元素的运算值”问题的快速解法

如果答案可以通过增量法快速求出，则可以：
用\(f[i][j]\)表示删除了i到j后剩余元素的运算值，通过\(f[i][j]\)求出\(f[i][mid]\)和\(f[mid+1][j]\)。总的时间复杂度为\(O(n\log nf(n))\)，其中\(f(n)\)为新增加一个元素的时间复杂度。
这个方法可以用在：

去除一个元素的高斯消元
不经过一个点的最短路

模意义下的矩阵消元(上三角化)

如果模数是素数：使用费马小定理求逆元进行除法。
如果模数不是素数：辗转相减。

LIS类问题的树上求解

利用multiset

求父节点权值>子节点权值，全局最多选几个点

对序列求lis时，我们可以将数字依次放进multiset中，每次新加入一个数字，删除其lower_bound，插入其本身。
对树求lis时，启发式合并每个字树的multiset，删除父节点lower_bound,插入父节点。

竞赛图

设D为有3个以上顶点的强连通竞赛图，则对于每个\(x\in V_D\)和每个整数\(k\in [3,n]\)都有一个k元环通过x。
任何一个竞赛图都含有一条Hamilton路
任何一个竞赛图包含Hamilton环当且仅当其联通

仅给出定理1的证明思路：
运用数学归纳法，当(n-1)个点的竞赛图满足定理1时，我们证明n个点的竞赛图也满足定理1.
添加一个点后，此点必定与之前的点的连边既有入边也有出边。假设全部都是出边，现给定一个入边。这样一定使该图存在一个n简单元环。然后证明对于该点存在[3,n-1]元环。
反证法：对于经过该点的k元环，确定之前n-1个点的n-1元环，那么在环上每隔k-1个点都必须与该点连入边。如果\(k-1\not| \ n-1\)，则一定可以找到这样的环。如果\(k-1|n-1\)，则通过这些连入边的点之间的连边，也一定可以找到一个k元环。

对于竞赛图类的问题，一般在拓扑排序后对图进行分析。

例题，test20180926，求双色边的竞赛图是否满足，每一种颜色的子图中都满足若存在\((u,v),(v,w)\)则一定存在\((u,w)\)。该题利用到如下结论：该性质存在当且仅当在一个子图中联通的两点在另一个子图中不连通，且每个子图不存在环。因此，将两个图正反合并在一起，找是否存在环即可。直接传递闭包最快是\(O(\frac{n^3}{\omega})\)的，而这种方法可以做到\(O(n^2)\)

点分治

由于动态点分治中子树之根并不连续，所以必须利用LCA求原树上的树上距离。
RMQ求LCA时需要在遍历子节点的同时不停在dfs序列内插入当前节点以维持最小值的准确。这样只会带来2的常数。

LCT

lct最灵活之处在于可以动态维护一棵树的形态(利用区间翻转标记)。

void access(int a)
{
	int b=0;
	while(a)
	{
		spl(a);
		tre[a].s[1]=b;
		upd(a);
		b=a;
		a=tre[a].f;
	}
}
void sroot(int a)
{
	access(a);
	spl(a);
	tre[a].rv^=1;
}
void cut(int a,int b)
{
	sroot(a);
	access(b);
	spl(b);
	tre[b].s[0]=tre[a].f=0;
	upd(b);
}
void link(int a,int b)
{
	sroot(a);
	tre[a].f=b;
}
int qmax(int a,int b)
{
	sroot(a);
	access(b);
	spl(b);
	return tre[b].mxp;
}

另外，动态树类问题中有两个比较常见的技巧：

如果需要维护点的连通性等问题（如同色联通块内的信息），可以对于每种颜色建立一棵LCT，原树中若\(u\)的颜色为白色，则在白色LCT中连边\((u,fa[u])\)。询问联通块答案时，只需要询问扣掉询问点所在LCT的根后，询问点所在的联通块的答案，即\(Access(x)\)后,\(Splay(root)\)，再询问\(root\)的右儿子信息即可。
如果需要维护Dp信息，可以采用如下方法：在Splay的每个节点\(x\)处维护两个值:\(fl,fr\)，分别表示\(x\)所在Splay对应的原树中的链最顶端和最低端的Dp信息。

尺取法

利用类似“毛毛虫”的一种解构维护一段连续的东西的方法。

如“最大连续字段和”,用左右两个端点维护中间的值最大。如果中间的值为负则收缩为0。
又如NOI2016"区间"，用左右两个端点维护当前可以产生m覆盖的所有区间。

这样，在平移这个“尺取”出的毛毛虫时，我们可以只是简单的处理左右端点的变化，这样可以依靠题目原本的单调性使总复杂度变成\(O(n*F(n))\)

分块枚举法：

对于一类需要多次进行“存储”与访问的操作，有时存储耗时多，而访问极其容易；或者访问耗时多，存储极其容易。

比如在一个数不超过\(10^{18}\)的集合里寻找x的倍数的个数，且已知所有数都是一个\(10^{18}\)以内数\(Y\)的约数，这时访问操作变成了\(O(n)\)或者\(O(\frac{10^{18}}{x})\)的了，而存储为\(o(1)\)，这时我们可以让存储让一步，使访问变快，最终两者速度达到平衡，利用均值不等式，我们知道两者复复杂度相近时总复杂度最低。

具体的做法是，将每个数分解质因数，将质因数划分为两个集合，使这两个集合可以组成的数的个数相近。对于一个\(X=A*B\)，我们将X的贡献加入到\(\forall b|B \ , \ f[A][b]\)中，查询时求\(\forall A|a \ , \ f[a][B]\)的和即可。如果\(Y\)的约数个数为\(\sigma\)，则存储和访问的时间复杂度都是\(O(\sqrt{\sigma})\)。

这样的问题，比如CTSC2017吉夫特，以及湖南省队集训2018陈江伦的一道题。

对合数取模的技巧

在一类问题中，如利用Burnside引理求本质不同的环染色方案数时

\[\begin{align} ans &= \frac{1}{n}\sum_{i=1}^{n} c^{gcd(i,n)} \\ &= \frac{1}{n}\sum_{d|n} c^{d}\phi(\frac{n}{d}) \end{align} \]

最终要将答案除以n，而只有在模素数意义下这个可以用逆元完成。所以我们可以在计算时对\(pn\)取模，最终将答案除以n即可。

同样，这个技巧可以利用于对合数取模的FWT中

一类数论问题的分析手段

1.约数个数函数

\[d(nm) = \sum _ {i|n} \sum _ {j|m} [gcd(i,j)=1] \\ \]

所以约数个数函数的二维前缀和可以这样化简：

\[\begin{align} \sum _ {n=1}^{N} \sum _ {m=1}^{N} d(nm) & = \sum _ {n=1}^{N} \sum _ {m=1}^{N} \sum _ {i|n} \sum _ {j|m} [gcd(i,j)=1] \\ & = \sum _ {i=1}^{N} \sum _ {j=1}^{N} \lfloor\frac{N}{i}\rfloor\lfloor\frac{N}{j}\rfloor [gcd(i,j)=1] \\ & = \sum _ {d=1} ^ {N} \mu(d) \sum _ {a=1} ^ {\lfloor\frac{N}{d}\rfloor} \sum _ {b=1} ^ {\lfloor\frac{N}{d}\rfloor}\lfloor\frac{N}{ad}\rfloor\lfloor\frac{N}{bd}\rfloor \end{align} \]

令\(f(n)=\sum _ {i=1} ^ {n} \lfloor\frac{n}{i}\rfloor\)
则

\[ \sum _ {n=1}^{N} \sum _ {m=1}^{N} d(nm) = \sum_{d=1}^{N}\mu(d)f(\lfloor\frac{N}{d}\rfloor)^2 \]

以上的玩意都可以\(O(N^\frac{3}{4})\)求解。如果预处理前\(O(N^\frac{2}{3}/\log^{\frac{1}{3}}n)\)个\(\mu(d)\)和\(f(d)\)，这东西就可以\(O(N^\frac{2}{3}\log^{\frac{1}{3}}n)\)求解了。

如果用线性筛预处理\(f(d),\mu(d)\)，可以做到\(O(n^\frac{2}{3})\)

如果\(N\leq 10^7\)有另外一种更快的方法：

\[\begin{align} \sum _ {n=1}^{N} \sum _ {m=1}^{M} d(nm) & = \sum _ {n=1}^{N} \sum _ {m=1}^{M} \sum _ {i|n} \sum _ {j|m} [gcd(i,j)=1] \\ & = \sum _ {n=1}^{N} \sum _ {m=1}^{M} \sum _ {i|n} \sum _ {j|m} \sum _ {d|i,d|j} \mu(d)\\ & = \sum _ {i=1}^{N} \sum _ {m=1}^{M} \sum _ {d|n,d|m} \mu(d)d(\frac{n}{d})d(\frac{m}{d})\\ & = \sum _ {d=1}^{N} \sum _ {a=1}^{\lfloor\frac{N}{d}\rfloor} \sum _ {b=1}^{\lfloor\frac{M}{d}\rfloor}d(a)d(b)\\ & = \sum _ {d=1}^{N} (\sum _ {a=1}^{\lfloor\frac{N}{d}\rfloor}d(a)) (\sum _ {b=1}^{\lfloor\frac{M}{d}\rfloor}d(b)) \end{align} \]

可以\(O(\sqrt{n})\)完成一次计算。

处理1e18大整数除以1e2小整数的问题

由于(long double)的精度无法满足这么大整数除以小整数的除法，因此我们可以采用如下战略：
首先得到大数与小数除法的整数部分，再用大数对小数的模值计算小数部分。

该方法被用在我对'ZJOI2015地震后的幻想乡'一题答案的处理上。

排列计数类DP的处理方式

对于一类Dp问题，通常要求出所有排列的种数。比如3个红球2个绿球组成了排列种数。

可以将每一种排列进行如下的编号(最小表示法)：从左往右数球，看见一个未出现过的颜色的球，若之前出现了\(i-1\)种颜色，将它编号为\(i\)。这样，每\(m!\)种排列对应一种最小表示法，因此最终的答案乘上\(m!\)即可。

该方法被用在YZOJ10015yyb和树。

区间求交

在一类为题的解决过程中，我们往往会需要求多个区间的交。有时，区间是会分段的，比如“求一条直线与所有已知直线相交”、或luogu U37667。这时，我们可以求补集的并，这个可以用排序完成统计。

剩余系问题与最短路

在剩余系中的一些问题，如求\(k\)的倍数中各个位数数字和的最小值，可以使用最短路解决。前面的问题的解答复杂度为\(O(k)\)。其具体方法是，将剩余系中的每个数看成一个节点，然后节点之间存在转移的边，意为已经有一个剩余系中的某个数，要获得另一个数的代价。然后从初始数字到终止数字的最短路就是答案。

前面的问题可以使用如下的方式建立\(O(k)\)的图。将一个数字乘\(10\),将一个数字加\(1\)。

积性函数线性筛

积性函数的狄利克雷卷积是积性函数。

证明：

\[\begin{aligned} (F*G)(ab) & =\sum_{d|ab}F(d)G(\frac{ab}{d})\\ & =\sum_{d|a,p|b}F(dp)G(\frac{ab}{pd})\\ & =\sum_{d|a,p|b}F(d)F(p)G(\frac{a}{d})G(\frac{b}{p})\\ & =(\sum_{d|a}F(d)G(\frac{a}{d}))(\sum_{d|b}F(d)G(\frac{b}{d}))\\ & =F(a)G(b) \end{aligned} \]

因此，积性函数卷积可以线性筛，积性函数点积显然也可以线性筛。

对于线性筛的函数，一般有如下处理方式：

1.找\(F(a\times p)\)在\(p|a\)与\(p\not|a\)情况下的取值。
2.求出\(F(p^k)\)，利用函数的积性求出\(F(\Pi p_i^{k_i})\)

或者可以

1.对于每个\(a\)，找到\(p^k|a\)，其中\(p\)为\(a\)最小的质因子，且\(k\)尽量大
\(F(a)=F(a/p^k)F(p^k)\)，不难证明在线性筛时\(F(a/p^k)\)和\(F(p^k)\)都已经筛出来了，因为它们的最小质因子都不超过\(p\)，而线性筛保证每个数被自己的最小质因子筛到，且按照递增顺序筛。

一类有决策单调性的Dp

dp有决策单调性，可以用cdq分治将时间复杂度优化为状态数的\(\log N\)倍。

用函数\(f(L, R) = [l, r]\)定义一个区间的转移区间，状态\([L, R]\)的转移区间为\([l, r]\)。

则，如果我们将区间\([L,R]\)的中点的转移点算出来，那么\([L,mid)\)和\((mid,R]\)的转移区间的无交并将是\([l,r]\)，这样，递归二分\([L,R]\)至多\(\log N\)层，每一层的区间即转移区间都恰好构成区间\([1,N]\)。因此总复杂度将是\(N\log N\)。

如果转移方程\(f[i]=f[j]+g(j+1,i)\)中的\(g\)难以计算，但是可以方便地像莫队一样维护，我们可以在递归的过程中维护\(g\),不难发现递归的每一层，左右端点移动的总次数不会超过\(4N\)(大概)，因此复杂度不变。

应该不存在更难转移的\(g\)了。更简单的\(g\)一般可以用前缀和、线段树等维护。

双栈排序

双栈排序指用两个栈和入栈、出栈两个操作，对一个排列排序。

两个元素不能放入同一个栈当且仅当：存在\(i<j<k,a[k]<a[i]<a[j]\)

1.\(n\leq 2000\)，dp找出不能在一个栈中的元素对，然后判断是否“不能在同一个栈中”的关系组成二分图。

2.\(n\leq 2\times 10^5\)，将二分图模型转成更普适的2-SAT模型，然后用可持久化线段树优化连边过程。空间复杂度 \(O(n\log n)\)，时间复杂度 \(O(n\log n)\)。且空间复杂度常数较大，\(10^5\)数据大约需要\(300MB\)空间。

3.只求出第一种做法中的二分图的一个生成树进行二分图染色，然后用类似第二种方法的一种方法判断是否可行，即所有可以连的边的两端的点颜色不同。求生成树可以用线段树动态维护某个点左边的所有联通块的编号，每次用线段树取出最大编号和最小编号的可行点，启发式合并它们的联通块。这样的时间复杂度\(O(n\log^2n)\)，空间复杂度\(O(n)\)。且时空复杂度常数都很小，因此整体上优于第二种方法。

4.同第三种方法，但是将所有元素映射到二维平面上，一个点需要与一个左侧无界的矩形区域内的所有点连边。按照一定顺序扫描可以保证这个矩形区域的右侧不降，下方不降，这样线段树就有点多余了，只需要用堆就可以了。

5.还可以使用并查集维护，时间复杂度\(O(n\alpha(n))\)，见http://uoj.ac/submission/332724

统计平方、方差的手段

方差=平方的平均数-平均数的平方

因此统计方差是建立在统计和、平方和的基础上的。

对于一类问题：如求所有子矩阵内点数的平方和，可以利用这种方法：一个集合内点数的平方和可以表示为一个集合内点对的个数。

统计不包含任何一个点/至少包含一个点的子矩阵个数

设k为点数：

\(O(k^2)\)方案：枚举每个“包含至少一个点的子矩阵”包含的最左边的点，然后用更左边的点限制矩阵的上下边界。

SAM中fail树层次遍历序的轻松获得

利用等价类最长长度进行基数排序，得到的就是层次遍历序，因为fail树父亲的长度短于儿子。但是不适用于广义SAM。

树上联通块计数类问题

如果要求包含根，可以转化为对偶图

如果不要求包含根，可以用点分治

树上的联通块数量也等于：包含每个点的联通块数量-包含每条边的联通块数量。原理：欧拉公式。

不支持在线的数据结构的在线化

可以采用二进制分组，用\(\log n\)个这样的数据结构替代一个大的可在线的数据结构。每当后一个数据结构大于前一个，就暴力合并这两个数据结构。

采用时间线段树可以支持时间区间询问。

有关同余的数学问题的解法

有两种思路，第一种基于复杂度分析，找到问题的分界点，当某个数的权值在\(\sqrt{n}\)上下时分别采用不同的方法。第二种是构造递归结构处理，如BZOJ1421，求\(L\leq xD\mod M\leq R\)的最小\(x\)。

有关图的连通性的题

可以枚举1所在的子集(或者枚举一个有代表性的子图，比如竞赛图中拓扑序最小的强连通分量)
可以花Bell数的时间枚举划分，然后斯特林容斥

以x为第一关键字，以y为第二关键字的最优化问题

将x乘上很大的权值与y相加，然后做单关键字最优化。

可以类比到凸优化问题。可以处理\(kx+by\)的最优化问题。

判断一条边在不在XXX内

最大匹配：观察这条边能否通过一个环将自己的流量转移到别的地方。跑完最大匹配后tarjan求出强连通分量，看这条边的两个端点是否在同一个强连通分量内。如果不在，则它必在最大匹配内，反之不一定在。也可以从未匹配点开始DFS，将所有可能通过增广路交换虚实的边打上标记，这些边可以出现在最大匹配内。剩下的边中的匹配边一定出现在最大匹配内。

最大权匹配：删边重做。

最大生成树：它负责连接的两个联通块间是否有同样权值的边。

查询被两个东西同时覆盖的元素个数：同时维护\(x+y\)和\(x^2+y^2\)，如CF-gym-102028

枚举拆分法

一些题目可能可以通过暴力枚举整数的拆分解决，其特征是对称性较强、等价情况较多、数据范围\(50\)左右。

如：BZOJ4671异或图，BZOJ1478Isomorphism

动态线性基：

方法1：时间线段树(需要离线)，复杂度带一个 \(\log\)

方法2：维护线性基的每个基向量是由哪几个原始向量组成的，每次删除一个向量，找出这个向量参与的基向量中最高位最低的一个，用这个向量异或其它被删除向量参与的基向量。现在其余的向量里都没有了这个被删除向量，并且线性基结构没有发生改变。现在只需要修改最高位最低的那个向量，再将其重新插入线性基即可。复杂度没有\(\log\)

状态压缩DP减少空间复杂度的技巧

由于一般的状态压缩dp的转移是一个分层图，只会存在相邻层之间的转移，我们不妨将每一层的状态拿出来单独保存，这样可以将空间复杂度从\(O(2^n)\)降低至\(O(\binom{n}{n/2})\)。

tarjan对拓扑排序的替代

tarjan后的编号即为拓扑序的反序。

形态不变的树的一个转化技巧

如SPOJ-QTREE6，可以将自己连向父亲的边的颜色设为自己的颜色。

用SAM可以\(O(cn)\)构建后缀数组

实测在随机数据下比基数排序树状数组慢一倍左右，但是卡树状数组数据下性能稳定，可以比树状数组快至少\(20\%\)

计数类问题的一些技巧

1.括号序列法：
- 将序列问题转化为括号序列问题。因为很多序列问题都满足“匹配”、“前缀为正”等常见的性质。这样，可以转化为括号序列问题进行计数。
- 一般来说，如果采用Dp的形式计数，我们会用\(f[i][j]\)中\(i\)表示前\(i\)位，\(j\)表示前缀和。这样两维的限制就可以满足“匹配”、“前缀为正”的性质。
- 如：Left Most Ball (ARC002F)，Permutation and Minimum (AGC030F)
2.二次统计法
- 如果需要维护二次方和，一般有两种常见套路：
- a.将二次方和用一次方和转移，即\((x+1)^2=x^2+2x+1\)，只需要分别维护展开后的每一项，就可以转移。
- b.将二次方拆成点对计数。比如说一段区间的“贡献”是平方，即在区间内放两个求的方案数。如Placing Squares (AGC013E)
- c.更复杂的问题也可以这样，比如51nod1947
3.联通块统计中的一个技巧
- Chords(AGC028D)中运用到了一个离奇的技巧：将圆周上的若干点之间两两配对并连线，每个点属于恰好一对内，如果两条线在圆内相交，则认为它们属于同一个联通块。现在已经有一些点之间存在固定的连线，求所有连线方法中联通块的数量和。
- 我们只需要统计存在多少个联通块的最小编号为\(l\)，最大编号为\(r\)。如果发生两个联通块的编号存在嵌套关系，则我们在统计小的联通块时将会获得小联通块的贡献，因此答案被补充不漏地统计到了。这样，在Dp的时候，就只需要保证枚举的这个联通块是“连通”的，而不需要考虑内部是否是“空心”的。这个技巧非常类似于欧拉定理，运用一个奇特的守恒关系巧妙地解决了问题。

一个有意思的对偶

将一个数拆分为\(k\)个数的方案，等价于拆分成不超过\(k\)的数。这两个问题可以用五边形数或者Dp求解。其中Dp方法为分块Dp。

另外，将一个数拆分为不超过\(k\)的不重复数字，等价于拆分成不超过\(k\)个连续数字。这两个问题可以用Dp求解。方法是：\(f[i][j]\)表示拆分为不超过\(k\)的不重复数字，前\(i\)个数和为\(j\)的方案数，其中\(i\leq \sqrt{n},j\leq n\)，支持两个转移：将所有数加\(i\)，或者将所有数加\(i\)，再最前面添\(1\)。注意当最后一个数大于\(k\)的时候需要容斥掉这个情况，即\(f[i][j]=f[i-1][j-i]+f[i][j-i]-f[i-1][j-(k+1)]\)

在线段树上一个区间内二分

一般的线段树上二分只针对整个线段树区间。如果需要在一个特定的区间内二分，找到“最靠右的满足某条件的值”，可以先像普通询问一样找到log个可能区间，在最右边的一个可能区间内二分。时间复杂度依旧是\(O(\log n)\)

提交答案题的一些技巧

如果是构造类问题，可以将题目给定的节点重载为自己熟悉的运算符。

pow(2,x)不会损失精度。

预处理矩阵的幂

分块预处理可以将矩阵快速幂的复杂度降到\(O(\sqrt{n}k^3+qk^3)\)

如果只需要求出答案矩阵的某个特定的行向量，不难发现，答案向量为一个矩阵和一个向量的积。因此我们分块预处理矩阵和向量，可以将复杂度降到\(O(\sqrt{n}k^{2.5}+qk^2)\)

如果只需要求答案矩阵的某个值，不难发现，答案即为两个向量的积。因此分块预处理两个向量即可，复杂度\(O(\sqrt{n}k^2+qk)\)

以上的方法基于如下的事实：\(A^n\vec{v}=A^{n-1}(A\vec{v})\)，为了得到\(A^n\vec{v}\)，我们只需要不停将\(v\)左乘矩阵\(A\)即可，复杂度仅为\(nk^2\)

支持在序列中间插入区间询问的数据结构

一个很容易想到的是平衡树。但是还有更简单的。

利用二进制分组，每一段连续时间内的插入被分到同一组，在合并两组时再去考虑后插入的元素如何“排挤”早插入的元素。

询问前缀时，从时间靠后的块开始询问，因为最后一个块内的元素插入时的位置就是它在真实序列中的位置，然后每次将询问的右端点减去当前块内在询问区间内的元素的个数，继续询问更早的块。

概率与期望的相关笔记

期望计算中的条件概率
- 给定黑白两种颜色的球共\(n\)个，每次给定随机两个球，将第一个球染成第二个球的颜色，求变成同色的期望步数。
- 设\(f[i]\)表示还有\(i\)个白球时，变成全白的概率，\(g[i]\)表示还有\(i\)个白球时，变成全白的条件下的期望。
- 则:

\[\begin{aligned} &\begin{cases} f[i]=\frac{f[i-1]+f[i+1]}{2}\\ f[0]=0\\ f[n]=1 \end{cases}\\ &\begin{cases} g[i]=\frac{n(n-1)}{2i(n-i)}+\frac{f[i-1]\times g[i-1]+f[i+1]\times g[i+1]}{f[i-1]+f[i+1]}\\ g[0]=\infty\\ g[n]=0 \end{cases} \end{aligned} \]

- 注意$g$的转移方程中按照$f$带权相加。

有关网格图的网络流

有时我们需要使图中一个点的度数要么为2要么为0，从而使这些点可以构成一个环。

这时可以采用如下的建图方式：

对于每个点\(i\)建立\(i_1\),\(i_2\)两个点。
连边\(S\rightarrow i_1\rightarrow i_2\rightarrow T\)
连边\(i_1\rightarrow j_2\)

然后强制最大流。

这样，一个点要么选择\(i_1\rightarrow i_2\)这条边自行解决，要么由一个点流入，再流出到另一个点。

约数和函数及约数个数函数

约数和函数\(\sigma(n)=O(n^{1/3})\)

约数个数函数\(d(n)=\Theta(\log n)\)

一个序列上的trick

前\(i\)个球至多选\(j\)个：等价于：第\(j+1\)个球至少在\(i+1\)处。

前\(i\)个球至少选\(j\)个：等价于：第\(j\)个球至多在\(i\)处。

如果要满足“第\(i\)个球在\([l_i,r_i]\)内”，我们只需要保证\([l_i,r_i](l_i\leq l_{i+1},r_i\leq r_{i+1})\)内有球即可，不需要保证这个球根其它球的位置关系。即它可能不是第\(i\)个，但最终我们选择的球再排序之后，一定满足条件。原因就是有\(l_i\leq l_{i+1},r_i\leq r_{i+1}\)这个条件。

请见Snuke the Phantom Thief(AGC031E)。

errors

20180223test:

其中(ll)在考试时忘记写上

for(int i=0;i<10;i++)tot=(tot+(ll)(b-a+2-ans[i])*(ll)ans[i]%MOD*(ll)mov(i)%MOD)%MOD;

网络流建图时边权变成了负数

for(int i=1;i<=g.n;i++)
{
	double wei=g.val[i]*k-g.hur[i];
	if(wei>=0)t.addeg(S,i,wei),t.addeg(i,S,0),possum+=wei;
	else t.addeg(i,T,-wei),t.addeg(T,i,0);      //考试时忘记写上负号
}

20180224:

K-D Tree删除节点

void destroy(int a)
{
	if(tre[a].s[0])destroy(tre[a].s[0]);
	tab[++num]=tre[a];
	delnode(a);                             //这样会导致tre[a]被删除，无法递归访问右子树
	if(tre[a].s[1])destroy(tre[a].s[1]);
}

20180311

误认为Splay节点x后原根节点一定是其儿子。原因是Splay双旋的特性使得父节点也会旋转。

20180502

LCT各种操作在access(x)完后仍需要splay(x)，原因是access操作形成了一棵维护根到x的路径的splay,此时x并不是根，需要旋转到根。

Pollard Rho

需要特判1，否则可能RE。

主席树可持久化并查集

不要路径压缩，这样会爆空间。
原因：达到了\(10^8\)级别。

Splay 在 insert 时, splay 插入的节点会使引用的变量改变，因为这个变量引用的是它的父亲的儿子变量。

缩点，1号节点编号不一定还是1

hash时一定要合并同类项，否则复杂度直接乘n

tarjan求点双联通分量时，栈的大小应该是边数，而不是点数

广义后缀自动机

广义后缀自动机不能用基数排序确定dfs序，因为存在节点的len相同，而互为父子关系。

动态开点的数据结构

尽量不出现：tre[a=++cnt]=tre[o]的语句，因为o和a可能是同一个东西，而a又是引用，会导致错误。

取模的注意事项

大数取模，加法可能会溢出
取模结果如果被用来做质数，模数需要减一

结构体构造函数

构造函数内千万不要放任何耗时的东西，如atan2

有关FFT

FFT时单位根每次重新算可以大大减少精度误差

有关空间限制

栈空间算在评测空间限制内，需要纳入考虑
栈空间大约是：递归深度(4+变量数)4/1024/1024 MB
Vector数组相比于3个元素的链表，有时使用的空间可能达到5倍之多(CF545div1C)

set等容器删除元素

for(auto i=st.begin(); i!=st.end()) st.erase(i++);      //正确
for(auto i=st.begin(); i!=st.end()) i=st.erase(i);      //正确
for(auto i=st.begin(); i!=st.end(); i++) st.erase(i);   //错误
for(auto i=st.begin(); i!=st.end()) i=st.erase(++i);    //错误
for(auto i : st) st.erase(i);                           //错误

其中网上流传的说法是：erase(i++)意为先找下一个迭代器再删除，erase(++i)是先删除再找迭代器。(即与通常的理解是反的)。

另外for(auto i : st)的写法在某些编译器下可以正确运行，但是某些不行。

字符串匹配

不停匹配一个字符

posted @ 2020-05-20 09:46 Jerx2y 阅读(104) 评论(0) 编辑收藏举报

刷新页面返回顶部

Why's Blog

旧试题