2024.11.20 NOIP模拟 - 模拟赛记录

异或（xor）

每次所加三角形的范围如图所示：

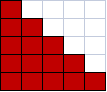
这道题做法较多，我是通过两组差分与前缀和来做的。

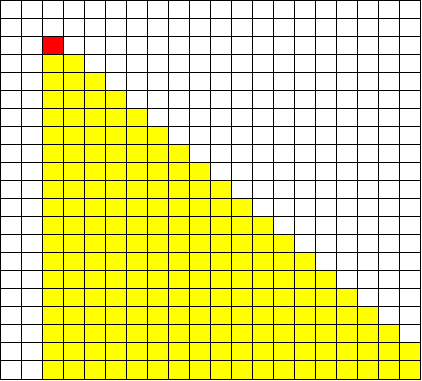
首先需要一个三角形差分，使每一次在差分数组中修改时，影响到的范围是一个三角形，比如这样（红色点为 \((x,y)\)，即 \((r,c)\)）：

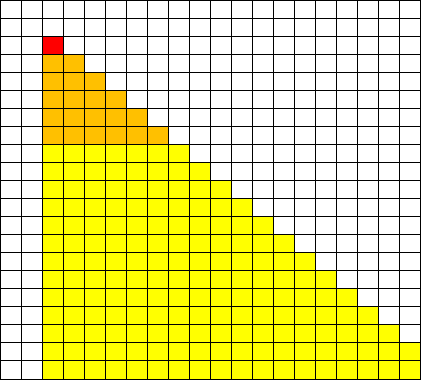
假设我们真正需要修改的三角形是橙色部分：

那么联系到正常差分，很容易想到在 \((x+l,y+l)\) 的位置减去多出的值：

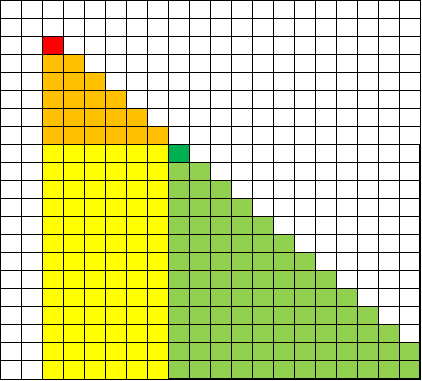
然而，左下方还多出了一块矩形，而这不是我们想要的，所以我们可以再额外维护一个矩形的二维差分来抵消这部分多出的贡献（像正常二维差分一样在这块矩形区域内全部减去多出的贡献即可）：

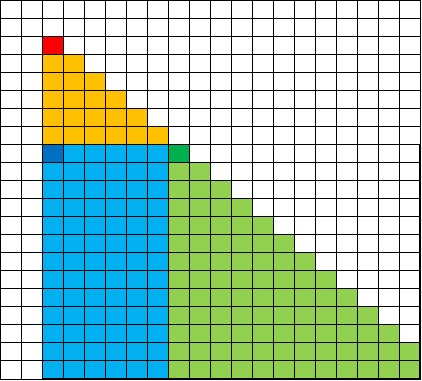
最后，对所有差分数组求前缀和，矩形差分数组的前缀和很好求，而三角形差分数组的前缀和则要额外注意。根据差分数组影响的三角形范围倒推可以得知，深蓝色部分的三角前缀和应该是这一部分的和：

其中深蓝色块的三角前缀和等于紫色块的三角前缀和加上深灰色部分，即（\(sum\) 表示三角前缀和，\(dif\) 表示差分数组）：

\[sum_{i,j}=sum_{i-1,j-1}+\sum_{k=1}^{i-1}dif_{k,j} \]

然后就做出来了，时间复杂度 \(O(N^2)\)：

#include<cstdio>
#include<algorithm>
#define LL long long
using namespace std;

const int N=1005;
int n,q;
LL tr_dif[N][N],sq_dif[N][N];
LL tr_sum[N][N],sq_sum[N][N];
//triangle, square 

inline void Add(int x,int y,int l,int s)
{
	tr_dif[x][y]+=s;
	if(x+l<=n&&y+l<=n) tr_dif[x+l][y+l]-=s;
	if(x+l<=n) sq_dif[x+l][y]-=s;
	if(x+l<=n&&y+l<=n) sq_dif[x+l][y+l]+=s;
	return;
}

void Calc_sum()
{
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			sq_sum[i][j]=sq_dif[i][j]+sq_sum[i-1][j]+sq_sum[i][j-1]-sq_sum[i-1][j-1];
	for(int j=1;j<=n;j++)
	{
		LL tmp=0;
		for(int i=1;i<=n;i++)
		{
			tmp+=tr_dif[i][j];
			tr_sum[i][j]=tr_sum[i-1][j-1]+tmp;
		}
	}
	return;
}

int main()
{
	freopen("xor.in","r",stdin);
	freopen("xor.out","w",stdout);
	
	scanf("%d%d",&n,&q);
	for(int i=1;i<=q;i++)
	{
		int x,y,l,s;
		scanf("%d%d%d%d",&x,&y,&l,&s);
		Add(x,y,l,s);
	}
	Calc_sum();
	LL ans=0;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			ans^=tr_sum[i][j]+sq_sum[i][j];
	printf("%lld\n",ans);
	return 0;
}

对于每一行维护一个差分的做法时间复杂度是 \(O(QN)\) 的，似乎也可以卡一卡。

游戏（game）

好啊，诈骗题是吧，Subtask 用上瘾了是吧！？

先说暴力，暴力就是枚举所有情况。具体来说，所以对于每一个 \(b_i\)，尝试进行操作一和操作二，得到两个结果，再根据当前角色是 Alice 还是 Bob 选择取这两个结果的最大或最小值返回（因为每一个人的策略是确定的，所以选择了操作以后，后面所得到的答案是确定的）。

时间复杂度 \(O(2^M \times N)\)，期望得分 \(15\) 分。

点击查看代码

const int M_s14=25;
bitset<M_s14> div[N],chs;
LL DFS(int p,bool r) //0A,1B
{
	if(p>m)
	{
		LL res=0;
		for(int i=1;i<=n;i++)
		{
			bool flag=true;
			for(int j=1;j<=m;j++)
				if((chs[j] && a[i]%b[j]) || (!chs[j] && a[i]%b[j]==0))
				{
					flag=false;
					break;
				}
			if(flag) res+=a[i];
		}
		return res;
	}
	chs[p]=true; LL res1=DFS(p+1,!r);
	chs[p]=false; LL res2=DFS(p+1,!r);
	if(r) return max(res1,res2);
	else return min(res1,res2);
}
void Solve()
{
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			if(a[i]%b[j]==0) div[i][j]=true;
	printf("%lld\n",DFS(1,0));
	return;
}

观察这一语句 if((chs[j] && a[i]%b[j]) || (!chs[j] && a[i]%b[j]==0)) 可以发现，对于某一个数，能够保留下它所需要的操作是确定的（因为两种操作互斥，所以能消掉它的操作都必须不选，不能消掉它的都必须选），所以我们可以预处理出保留某一个数所需要的操作序列，用类似状态压缩的方式储存下来，这样就不用每次都遍历所有 \(n\) 个元素了。

时间复杂度 \(O(2^M)\)，期望得分 \(30\) 分。

点击查看代码

const int M_s14=20;
LL sum[1<<(M_s14+1)];
LL DFS(int p,unsigned int chs) //0A,1B
{
	if(p>=m) return sum[chs];
	LL res1=DFS(p+1,chs);
	LL res2=DFS(p+1,chs|1<<p);
	if(p&1) return max(res1,res2);
	else return min(res1,res2);
}
void Solve()
{
	for(int i=1;i<=n;i++)
	{
		unsigned int div=0;
		for(int j=1;j<=m;j++)
			if(a[i]%b[j]==0) div|=1<<(j-1);
		sum[div]+=a[i];
	}
	printf("%lld\n",DFS(0,0));
	return;
}

对于特殊性质“所有的 \(b_i\) 都相等”，这是我赛事的草稿，讲得还算清楚：

最后一步：
A: \(\min(0,sum)\)
B: \(\max(0,sum)\)

倒数第二步：
A: 和为正数-直接干成 \(0\)（否则 B 在最后一步会搞出正数）
和为负数-保留，但B最后还是会弄成 \(0\)
B: 和为负数-直接干成 \(0\)（否则 A 在最后一步会搞出负数）
和为正数-保留，但A最后还是会弄成 \(0\)

综上所述：在倒数第二步，和为正数、零、负数最后都会被干成 \(0\)
故步数 \(\ge 2\) 时答案必为 \(0\)

特判：步数 \(=1\) 时：A 先手，直接取 \(\min\)(\(b\) 倍数和、非 \(b\) 倍数和)

点击查看代码

void Solve()
{
	if(m==1)
	{
		LL b_sum=0,nb_sum=0;
		for(int i=1;i<=n;i++)
		{
			if(a[i]%b[1]) nb_sum+=a[i];
			else b_sum+=a[i];
		}
		printf("%lld\n",min(b_sum,nb_sum));
	}
	else printf("0\n");
	return;
}

上面的做法是没有前途的。

我们需要回归最原始的暴力：直接模拟题意，某一步需要删除数的时候就真的把它删掉，附代码：

点击查看代码

LL DFS(int p,const vector<LL> &src)
{
	if(p>m)
	{
		LL res=0;
		for(LL x:src) res+=x;
		return res;
	}
	vector<LL> nxt;
	for(LL x:src) if(x%b[p]==0) nxt.push_back(x);
	LL res1=DFS(p+1,nxt);
	nxt.clear();
	for(LL x:src) if(x%b[p]!=0) nxt.push_back(x);
	LL res2=DFS(p+1,nxt);
	return p&1?min(res1,res2):max(res1,res2);
}

还有一个很重要的剪枝：当集合已经为空时，因为元素无法增多，所以这时可以直接返回 \(0\)，在代码中加入一行 if(src.empty()) return 0; 即可。

通过然后这个暴力的时间复杂度就成功地来到了 \(O(NM)\)。

具体分析：

每一次递归将当前集合分割成两个互斥的集合（题目所给两个操作互斥），画出递归树可以发现，如果将递归以处理到的操作位置（即上面代码中的 \(p\)）分层，那么每一层所处理集合的总大小都为 \(n\)。因为递归最多 \(m\) 层，所以时间复杂度就是 \(O(NM)\)。

题解上面有一段话（请忽略那句吐槽）：

理解一下这句话：对于玩家 Alice，如果她始终在每一次操作中都在两个部分中选择较小的那一个部分（这一部分大小一定小于等于原集合总大小的一半），那么在她操作 \((\log n +1)\) 次后，集合一定会被缩成空，答案是 \(0\)。

这并不是说她一定要这么选，而是她一定有一种选择方式把结果推成 \(0\)，而这种选择方式无关 Bob 的选择。也就是说如果 Alice 能够操作大于等于 \(\log n\) 次，那么最后的答案一定不会大于 \(0\)。

对于 Bob 也是同理，如果他可以操作 \(\log n\) 次，也可以用同样的策略把答案推成 \(0\)，最后的答案一定不会小于 \(0\)。

综上所述，如果 Alice 和 Bob 都能操作至少 \(\log n\) 次，即 \(m \ge 2 \log n\) 时，答案不小于 \(0\) 也不大于 \(0\)，也就只能是 \(0\) 了。

判断了这个以后，就可以 AC 了，而且跑得飞快。代码超短的：

#include<cstdio>
#include<vector>
#define LL long long
using namespace std;

const int N=2e4+5,M=2e5+5;
int n,m;
LL a[N],b[M];

LL DFS(int p,const vector<LL> &src)
{
	if(p>m)
	{
		LL res=0;
		for(LL x:src) res+=x;
		return res;
	}
	if(src.empty()) return 0;
	vector<LL> nxt;
	for(LL x:src) if(x%b[p]==0) nxt.push_back(x);
	LL res1=DFS(p+1,nxt);
	nxt.clear();
	for(LL x:src) if(x%b[p]!=0) nxt.push_back(x);
	LL res2=DFS(p+1,nxt);
	return p&1?min(res1,res2):max(res1,res2);
}

int main()
{
	freopen("game.in","r",stdin);
	freopen("game.out","w",stdout);
	
	scanf("%d%d",&n,&m);
	if(m>28){printf("0\n");return 0;}
	for(int i=1;i<=n;i++)
		scanf("%lld",&a[i]);
	for(int i=1;i<=m;i++)
		scanf("%lld",&b[i]);
	vector<LL> init(a+1,a+n+1);
	printf("%lld\n",DFS(1,init));
	return 0;
}