2024.11.18 NOIP模拟 - 模拟赛记录
密文板(ciphertext)
简单模拟,以下面的括号序列为例:
`?))?((?)()?)?)(?)?()??)(?)?)()??)(`
首先把所有可以合并的括号合并了,因为交错合并的括号一定可以正常合并(例如交错合并的 \(\textcolor{green}{(} \textcolor{blue}{(} \textcolor{green}{)} \textcolor{blue}{)}\) 可以以 \(\textcolor{green}{(}\textcolor{blue}{()} \textcolor{green}{)}\) 的正常顺序合并),所以这样做不会影响后续的合并。
?))? ? ? ?) ? ? ??) ? ?) ??)(
然后对于所有的单边括号,试图用一个 ? 来与其匹配。
())? ? ? () ? ? ?() ? () ?()( )? ? ? ? ? ? ? ? (
这时还剩下的括号就是无法消去的括号,不用管它,只用把剩下的 ? 两个一组合并起来。
)( ) ( ) ( ) ( ) ( ) (
最后的结果就是:
())((())()()()())(())()(()()())()(
完整合并过程:
0. ?))?((?)()?)?)(?)?()??)(?)?)()??)( 1. ?))? ? ? ?) ? ? ??) ? ?) ??)( 2. ())? ? ? () ? ? ?() ? () ?()( 2. )? ? ? ? ? ? ? ? ( 3. )( ) ( ) ( ) ( ) ( 3. ) ( *. ())((())()()()())(())()(()()())()( 最终结果 *. ) ( 不可合并
#include<cstdio> #include<cstring> #include<bitset> using namespace std; const int N=1e5+5; int n; char s[N]; char ans[N]; int sta[N],top; bitset<N> done; inline void clear_sta() { while(top) sta[top--]=0; return; } int main() { freopen("ciphertext.in","r",stdin); freopen("ciphertext.out","w",stdout); int T; scanf("%d",&T); while(T--) { scanf("%d%s",&n,s+1); for(int i=1;i<=n;i++) { if(s[i]=='(') { ans[i]=s[i]; sta[++top]=i; } if(s[i]==')') { ans[i]=s[i]; if(top) done[sta[top--]]=done[i]=true; } } clear_sta(); for(int i=1;i<=n;i++) //'(' { if(done[i]) continue; if(s[i]=='(') sta[++top]=i; if(s[i]=='?' && top) { ans[i]=')'; done[sta[top--]]=done[i]=true; } } clear_sta(); for(int i=n;i>=1;i--) //')' { if(done[i]) continue; if(s[i]==')') sta[++top]=i; if(s[i]=='?' && top) { ans[i]='('; done[sta[top--]]=done[i]=true; } } clear_sta(); for(int i=1;i<=n;i++) { if(done[i]) continue; if(s[i]=='?') { if(top) { ans[i]=')'; done[sta[top--]]=done[i]=true; } else { ans[i]='('; sta[++top]=i; } } } clear_sta(); int cnt=n,tmp=0; for(int i=1;i<=n;i++) { if(ans[i]=='(') tmp++; if(ans[i]==')' && tmp) { tmp--; cnt-=2; } done[i]=false; } printf("%d\n%s\n",cnt,ans+1); } return 0; }
挑战NPCⅢ(color)
数组开小挂 \(20\) 分,呜呜呜。
我的做法十分神奇,首先因为原图是超稀疏图,所以在原图上根据 DFS 序建树,根据深度先赋予一个颜色(奇数层赋 \(1\),偶数层赋 \(2\))。
然后把不在树上的边(最多 \(k \le 8\) 条边)所连的点全部取下来,这些点需要重新赋值,暴力枚举所有的赋值情况,对于每一个都判断一下。
只是不知道是做法假了还是写挂了,可能会有点过不去,加个随机数随机一下建出来的树和起点就好了。
#include<cstdio> #include<bitset> #include<random> #include<chrono> #include<algorithm> using namespace std; namespace IO{ #ifndef JC_LOCAL const int SIZE=1<<20; char buf[SIZE],*p1=buf,*p2=buf; #define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,SIZE,stdin),p1==p2)?EOF:*p1++) #endif template<typename TYPE> void read(TYPE &x) { x=0; bool neg=false; char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')neg=true; ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+(ch^'0'); ch=getchar();} if(neg){x=-x;} return; } template<typename TYPE> void write(TYPE x) { if(x==0){putchar('0');return;} if(x<0){putchar('-');x=-x;} static int sta[50]; int statop=0; while(x){sta[++statop]=x%10;x/=10;} while(statop){putchar('0'+sta[statop--]);} return; } template<typename TYPE> inline void write(TYPE x,char ch){write(x),putchar(ch); return;} } using namespace IO; int ID; const int N=1e5+5,K=5,T=10,M=(N+T)<<1; int n,m,k,t; int col[N]; bool have_ans; pair<int,int> raw[M]; struct Allan{ int to,nxt; }edge[M]; int head[N],idx; inline void add(int x,int y) { edge[++idx]={y,head[x]}; head[x]=idx; return; } namespace K1{ void Solve() { if(n==1) have_ans=true,col[1]=1; else have_ans=false; return; } } namespace K2{ void DFS(int x) { for(int i=head[x];i;i=edge[i].nxt) { int y=edge[i].to; if(col[y]) { if(col[y]==col[x]) have_ans=false; continue; } col[y]=col[x]==1?2:1; DFS(y); if(!have_ans) break; } return; } void Solve() { have_ans=true; col[1]=1; DFS(1); return; } } //namespace K2 namespace K3{ int dep[N]; bool vste[M]; void DFS(int x) { for(int i=head[x];i;i=edge[i].nxt) { int y=edge[i].to; if(dep[y]) continue; dep[y]=dep[x]+1; vste[i]=vste[(i&1)?i+1:i-1]=true; DFS(y); } return; } int redo[N],redo_idx; bitset<N> in_redo; bool check(int x,bool include_redo) { for(int i=head[x];i;i=edge[i].nxt) { int y=edge[i].to; if(!include_redo && in_redo[y]) continue; if(col[y]==col[x]) return false; } return true; } void Reset(int p) { if(p>redo_idx) { bool flag=true; for(int i=1;i<=redo_idx;i++) if(!check(redo[i],true)) {flag=false; break;} if(flag) have_ans=true; return; } for(int i=1;i<=3;i++) { col[redo[p]]=i; if(check(redo[p],false)) { Reset(p+1); if(have_ans) break; } } return; } void ClearData() { for(int i=1;i<=redo_idx;i++) redo[i]=0; redo_idx=0; for(int i=1;i<=n;i++) { in_redo[i]=false; dep[i]=0; col[i]=0; } for(int i=1;i<=idx;i++) vste[i]=false; return; } void Solve(int src) { ClearData(); dep[src]=1; DFS(src); for(int i=1;i<=n;i++) col[i]=((dep[i]-1)&1)+1; for(int x=1;x<=n;x++) for(int i=head[x];i;i=edge[i].nxt) if(!vste[i]) { int y=edge[i].to; if(!in_redo[x]) redo[++redo_idx]=x; if(!in_redo[y]) redo[++redo_idx]=y; in_redo[x]=in_redo[y]=true; } Reset(1); return; } } //namespace K3 int main() { freopen("color.in","r",stdin); freopen("color.out","w",stdout); read(ID); read(n),read(m),read(k),read(t); t=m-n; for(int i=1;i<=m;i++) read(raw[i].first),read(raw[i].second); mt19937 engine(chrono::steady_clock::now().time_since_epoch().count()); shuffle(raw+1,raw+m+1,engine); for(int i=1;i<=m;i++) add(raw[i].first,raw[i].second),add(raw[i].second,raw[i].first); if(k==1) K1::Solve(); if(k==2) K2::Solve(); if(k==3) { for(int i=1;i<=100;i++) { K3::Solve(engine()%n+1); if(have_ans) break; } } if(have_ans) { write(1,'\n'); for(int i=1;i<=n;i++) write(col[i],' '); putchar('\n'); } else write(-1,'\n'); return 0; }
escape from whk 3(kuhu)
你觉得我会打正解吗?不可能的。
赛时暴力,直接枚举区间内数的选择情况,时间复杂度 \(O(M \times 2^N \times N^2)\)
点击查看代码 · $10$ 分
int l,r; int ans; bitset<N> chs,invalid; void DFS(int p) { if(p>r) { bool is_valid=true; for(int i=l;i<=r;i++) { if(!chs[i]) continue; for(int j=l;j<=r;j++) { if(!chs[j] || j==i) continue; if(invalid[i+j]) { is_valid=false; break; } } if(!is_valid) break; } if(is_valid) { int cnt=0; for(int i=l;i<=r;i++) if(chs[i]) cnt++; ans=max(ans,cnt); } return; } chs[p]=false; DFS(p+1); chs[p]=true; DFS(p+1); return; } void Solve() { for(int i=0;(1<<i)<=(n<<1);i++) invalid[1<<i]=true; for(int i=1;i<=m;i++) { scanf("%d%d",&l,&r); ans=0; DFS(l); printf("%d\n",ans); } printf("%d\n",num); return; }

有图有真相! \(l=1,r=20\) 时构建出来的森林大概长成这个样子,加粗的是最优解选择的点:
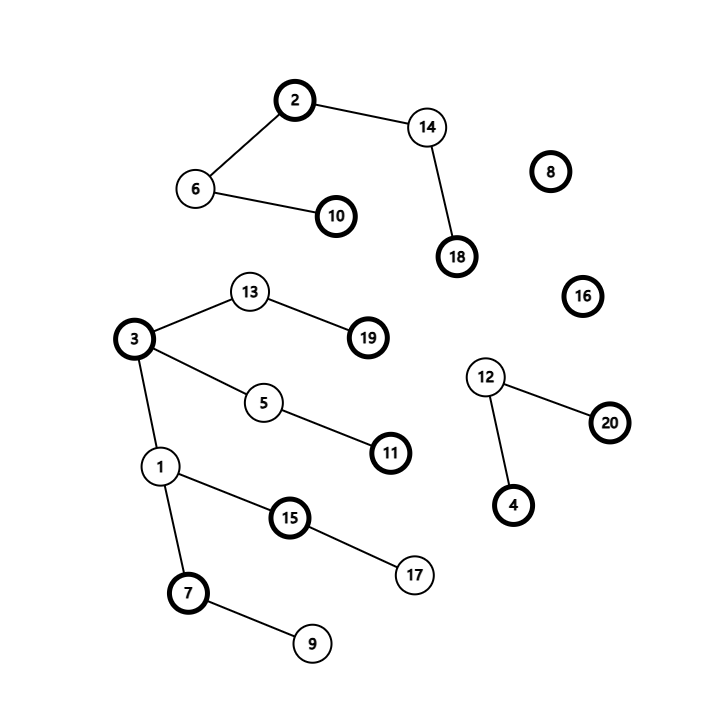
然而并不需要树上 DP 那么高级的玩意,只需要统计每个森林中奇数层和偶数层分别有多少个点,然后取最大值就是这棵树上的最大独立集,对所有树求和即可。
而且这样做后面也不需要各种容斥和各种加减 DP 贡献(就是因为 DP 做法后面脑子要烧坏才没有用它的)。
点击查看代码 · $35$ 分
struct Allan{ int to,nxt; }edge[N]; int head[N],idx; void add(int x,int y) { edge[++idx]={y,head[x]}; head[x]=idx; return; } int dep[N]; int cnt0=0,cnt1=0; void DFS(int x) { if(dep[x]&1) cnt1++; else cnt0++; for(int i=head[x];i;i=edge[i].nxt) { int y=edge[i].to; if(dep[y]) continue; dep[y]=dep[x]+1; DFS(y); } return; } int jc_log2(int x) { int res=0; while(x) x>>=1,res++; return res; } int fa[N]; int Calc(int l,int r) { for(int i=l;i<=r;i++) if(fa[i]>=l) add(fa[i],i),add(i,fa[i]); int res=0; for(int i=l;i<=r;i++) if(!dep[i]) { dep[i]=1; cnt0=0,cnt1=0; DFS(i); res+=max(cnt0,cnt1); } for(int i=l;i<=r;i++) head[i]=dep[i]=0; idx=0; return res; } void Solve() { for(int i=1;i<=n;i++) { int t=1<<jc_log2(i); if(0<t-i&&t-i<i) fa[i]=t-i; } for(int i=1;i<=m;i++) { int l,r; scanf("%d%d",&l,&r); printf("%d\n",Calc(l,r)); } if(num) { long long sum=0; for(int i=1;i<=n;i++) for(int j=i;j<=n;j++) sum+=Calc(i,j); printf("%lld\n",num*sum); } else printf("0\n"); return; }
临时去学习了一下莫队,思想很简单,引用一下 OI Wiki:

本题中要使用莫队需要实现三个操作:
- \(R\) 右移,即在右侧加入元素
- \(R\) 左移,即在右侧删除元素
- \(L\) 右移,即在左侧删除元素
(因为 \(l\) 有序,所以不需要 \(L\) 左移的操作)
其中最右边的节点一定是叶子结点,而最左边的一定是根节点(因为每一个结点的父结点值都比自己小)。
要实现上述操作,还需要记录一些内容:\(i\) 的所有子节点集合 \(son_i\)(\(son_i\) 的大小为 \(\log n\) 级别),点 \(i\) 的父结点 \(fa_i\);以 \(i\) 为根的子树中,位于奇数层的结点数量 \(f_{i,1}\) 与位于偶数层的结点数量 \(f_{i,0}\)(自己为0层),答案只需要统计所有根的 \(\max\{f_{i,0},f_{i,1}\}\)。
-
\(R\) 右移,即在右侧加入叶结点 \(x\):首先需要找到 \(x\) 所在树的根结点 \(root\),先将当前答案 \(now\) 减去 \(root\) 的贡献 \(\max\{f_{root,0},f_{root,1}\}\);然后更新从 \(x\) 到 \(root\) 路径上所有点的 \(f\) 值(对应 \(f_{i,0}\) 或 \(f_{i,1}\) 加一),最后再用新的 \(\max\{f_{root,0},f_{root,1}\}\) 来更新答案。
-
\(R\) 左移,即删除叶结点 \(x\):与上面的处理过程相似,先找到根 \(root\) 并减去原来的贡献,然后从 \(x\) 走到 \(root\),更新路径上的 \(f\) 值(对应 \(f_{i,0}\) 或 \(f_{i,1}\) 减一),最后再用 \(root\) 新的 \(f\) 值更新答案。
-
\(L\) 左移,即删除一个根 \(x\):先减去以 \(x\) 为根子树的答案 \(\max\{f_{x,0},f_{x,1}\}\),然后遍历它的所有子结点,将当前答案加上每一个子结点 \(y\) 的最大独立集的大小 \(\max\{f_{y,0},f_{y,1}\}\)。
有了以上三个操作,就可以 \(O(\log N)\) 地转移答案区间,总时间复杂度 \(O(N \sqrt{N} \log N)\)。
特别注意,应该优先扩大答案区间,然后再缩小答案区间。
\(65\) 分代码:
#include<cstdio> #include<bitset> #include<vector> #include<algorithm> using namespace std; const int N=3e5+5,M=3e5+5; int n,m,num; int L,R; int fa[N]; int f[N][2]; //以i为根的子树中,奇数层与偶数层的结点数量(自己为0层) vector<int> son[N]; int now; void Build() { for(int i=1;i<=n;i++) f[i][0]=f[i][1]=0; L=R=1; f[1][0]=1,now=1; return; } int Calc(int l,int r) { // printf("Calculating [%d,%d]\n",l,r); while(R<r) //R++ 加右(叶) { R++; int x=R; int root=x; while(L<=fa[root]&&fa[root]<=R) root=fa[root]; now-=max(f[root][0],f[root][1]); bool lv=0; while(x!=root) { f[x][lv]++; x=fa[x],lv^=1; } f[root][lv]++; now+=max(f[root][0],f[root][1]); } while(L<l) //L++ 删左(根) { int x=L; now-=max(f[x][0],f[x][1]); for(int y:son[x]) if(L<=y&&y<=R) now+=max(f[y][0],f[y][1]); f[x][0]=f[x][1]=0; L++; } while(R>r) //r-- 删右(叶) { int x=R; int root=x; while(L<=fa[root]&&fa[root]<=R) root=fa[root]; now-=max(f[root][0],f[root][1]); bool lv=0; while(x!=root) { f[x][lv]--; x=fa[x],lv^=1; } f[root][lv]--; now+=max(f[root][0],f[root][1]); R--; } return now; } int jc_log2(int x) { int res=0; while(x) x>>=1,res++; return res; } pair<pair<int,int>,int> q[M]; int ans[M]; int main() { freopen("kuhu.in","r",stdin); freopen("kuhu.out","w",stdout); scanf("%d%d%d",&n,&m,&num); for(int i=1;i<=n;i++) { int t=1<<jc_log2(i); if(0<t-i&&t-i<i) { fa[i]=t-i; son[t-i].push_back(i); } } for(int i=1;i<=m;i++) { int l,r; scanf("%d%d",&l,&r); q[i]={{l,r},i}; } sort(q+1,q+m+1); Build(); for(int i=1;i<=m;i++) { int l=q[i].first.first,r=q[i].first.second; ans[q[i].second]=Calc(l,r); } for(int i=1;i<=m;i++) printf("%d\n",ans[i]); if(num) { if(n==20000&&m==20000) printf("873721034680\n"); else { Build(); long long sum=0; for(int i=1;i<=n;i++) for(int j=i;j<=n;j++) sum+=Calc(i,j); printf("%lld\n",num*sum); } } else printf("0\n"); return 0; }
伤痕累累的心, 在暴雨中仍然放声歌唱(scar)
什么诡异的题目名
暴力 \(+1\)。
#include<cstdio> using namespace std; //Cartesian Tree const int N=2e5+5; int n,a[N]; namespace Data_1234{ int ls[N],rs[N]; int sz[N]; long long ans; void DFS(int x) { sz[x]=1; if(ls[x]) { DFS(ls[x]); sz[x]+=sz[ls[x]]; } if(rs[x]) { DFS(rs[x]); sz[x]+=sz[rs[x]]; } if(x) ans+=sz[x]; return; } int sta[N],top; int b[N],bidx; void Solve() { for(int k=1;k<=n;k++) { for(int i=1;i<=n;i++) if(a[i]<=k) b[++bidx]=a[i]; for(int i=1;i<=bidx;i++) { while(top && b[sta[top]]<b[i]) sta[top--]=0; ls[i]=rs[sta[top]]; rs[sta[top]]=i; sta[++top]=i; } DFS(0); printf("%lld\n",ans); for(int i=0;i<=bidx;i++) b[i]=ls[i]=rs[i]=sz[i]=0; ans=bidx=0; while(top) sta[top--]=0; } return; } } //namespace Data_1234 namespace Data_5{ void Solve() { long long ans=0; for(int i=1;i<=n;i++) { ans+=i; printf("%lld\n",ans); } return; } } namespace Cheat{ void Solve() { Data_1234::Solve(); return; } } int main() { freopen("scar.in","r",stdin); freopen("scar.out","w",stdout); scanf("%d",&n); bool is_d5=true; for(int i=1;i<=n;i++) { scanf("%d",&a[i]); if(a[i]!=i) is_d5=false; } if(n<=2000) Data_1234::Solve(); else if(is_d5) Data_5::Solve(); else Cheat::Solve(); return 0; }
本文采用 「CC-BY-NC 4.0」 创作共享协议,转载请注明作者及出处,禁止商业使用。
作者:Jerrycyx,原文链接:https://www.cnblogs.com/jerrycyx/p/18553600




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步