AcWing 1078. 旅游规划 （DFS找树的直径+直径中点性质求解，无DP）

原题链接

题目描述

---

算法

引用自 树的直径 - OI-Wiki：

若树上所有边边权均为正，则树的所有直径中点重合
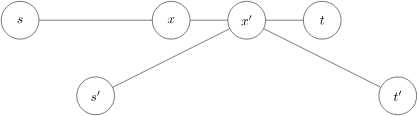
证明：使用反证法。设两条中点不重合的直径分别为 \(\delta(s,t) 与 \delta(s',t')\)，中点分别为 \(x\) 与 \(x'\)。显然，\(\delta(s,x) = \delta(x,t) = \delta(s',x') = \delta(x',t')\)。

有 \(\delta(s,t') = \delta(s,x) + \delta(x,x') + \delta(x',t') > \delta(s,x) + \delta(x,t) = \delta(s,t)\)，与 \(\delta(s,t)\) 为树上任意两节点之间最长的简单路径矛盾，故性质得证。

补充说明：当树的直径长度为偶数的时候，所有直径必定经过两中点及其间的边，证明与上文类似。

根据以上内容，所有直径必过中点且一定以其为自己的中点，所以总体思路为找到中点后，从中点出发找到与中点距离为直径一半的点，即为直径一端点

所以，我们可以两次 DFS 找出树直径的两端点，然后再一次 DFS 找到树的直径的一个或两个中点（已知直径两端点之间路径上距离一端点 直径>>1 或 (直径+1)>>1 的点，可能有两个中点），最后从一个或两个中点分别 DFS 找与中点距离为直径一半的点，找到后回溯时把路径上所有点都打上标记，最后输出有标记的点即可。

注意一个细节：当有两个中点时，为了避免多找或漏找，可以在将判断条件设置为 距离>=(直径+1)>>1，这样当直径为偶数时（此时中点只有一个）+1 不影响判断；当直径为奇数（此时有两个中点），向上取整可以使每一个中点都找到更靠近另一个中点的端点。否则如果不向上取整的话，可能找到在另一个中点那边距离自己 直径>>1 的点，但实际上直径应当是自己这边的一端距离自己 直径>>1，另一个中点的那一端距离自己 (直径+1)>>1（即距离另一个中点 直径>>1），所以会把不是端点的点判为端点，就 WA 了（被这个坑了好几次）。

时间复杂度

五次 DFS 均为 \(O(N)\)，总时间复杂度为 \(O(N)\)

C++ 代码

#include<cstdio>
#include<cstring>
using namespace std;

const int N=2e5+5;
int n;

struct Allan{
	int to,nxt;
}edge[N<<1];
int head[N],idx;
inline void add(int x,int y)
{
	edge[++idx]={y,head[x]};
	head[x]=idx;
	return;
}

void DFS_in(int *len,int x,int fa=0)
{
	for(int i=head[x];i;i=edge[i].nxt)
	{
		int y=edge[i].to;
		if(y==fa) continue;
		len[y]=len[x]+1;
		DFS_in(len,y,x);
	}
	return;
}

int pos1,pos2,diam,core1,core2;
int len_core[N];
bool is_diam[N];
bool DFS_find_path(int x,int fa=0)
{
	if(len_core[x]>=(diam+1)>>1)
		return is_diam[x]=true;
	bool on_diam=false;
	for(int i=head[x];i;i=edge[i].nxt)
	{
		int y=edge[i].to;
		if(y==fa) continue;
		len_core[y]=len_core[x]+1;
		on_diam|=DFS_find_path(y,x);
	}
	is_diam[x]|=on_diam;
	return on_diam;
}

int len1[N],len2[N];
bool DFS_find_core(int x,int fa=0)
{
	if(x==pos2) return true;
	bool on_diam=false;
	for(int i=head[x];i;i=edge[i].nxt)
	{
		int y=edge[i].to;
		if(y==fa) continue;
		on_diam|=DFS_find_core(y,x);
		if(on_diam&&len2[x]==diam>>1) core1=x;
		if(on_diam&&len2[x]==(diam+1)>>1) core2=x;
	}
	return on_diam;
}

int main()
{
	scanf("%d",&n);
	for(int i=1;i<n;i++)
	{
		int x,y; scanf("%d%d",&x,&y);
		x++,y++;
		add(x,y),add(y,x);
	}
	DFS_in(len1,1);
	for(int i=1;i<=n;i++)
		if(len1[i]>len1[pos1]) pos1=i;
	DFS_in(len2,pos1);
	for(int i=1;i<=n;i++)
		if(len2[i]>len2[pos2]) pos2=i;
	diam=len2[pos2];
	DFS_find_core(pos1);
	DFS_find_path(core1);
	memset(len_core,0,sizeof(len_core));
	DFS_find_path(core2);
	for(int i=1;i<=n;i++)
		if(is_diam[i]) printf("%d\n",i-1);
	return 0;
}