数据结构与算法之2-3-4树

数据结构与算法之2-3-4树

原文来自个人博客(求访问/关注/收藏): https://bbing.com.cn/ CNBLOG个人博客不定期转载

平衡树

不太平衡的二叉树

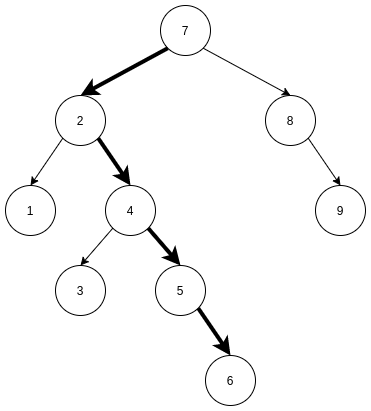
对于一个普通的二叉查找树, 我们可以发现一个问题, 存在一定的可能性, 一般的二叉查找树会退化成一般的链表.

上图还没有完全退化, 但是如果查找6这个结点, 会比其他的叶子结点走更多的路程.

为了解决一般二叉查找树可能带来的退化问题, 引入了平衡树的概念.

完全二叉树和满二叉树是平衡树.

平衡树的定义就是: 左右子树的高度差不大于1的树.

2-3-4树

2-3-4树

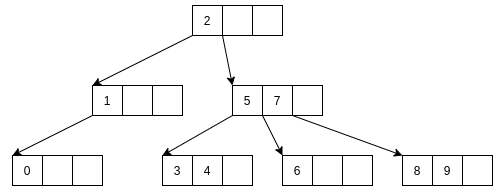
2-3-4树的意思就是二叉/三叉/四叉树.

简单起见, 可以把2-3-4树定义为四叉树, 一个结点可以存储三个元素和四个孩子结点的指针.

如上图, 先约定左中右三个元素代号是A, B, C; 从左到右的四个孩子结点的指针是a, b, c, d.

可以看到, 每个结点元素不一定要填满, 每个子结点指针也不一定要填满.

查找

和二叉查找树类似, 每个结点的子树也是根据元素与结点大小划分的.

  • a指向P < A的子树;
  • b指向A < P < B的子树;
  • c指向B < P < C的子树;
  • d指向C < P的子树;

所以, 查找一个结点的时候, 根据被查找元素P与A/B/C的大小关系, 走不同的路径来查找元素.

以下, 是查找元素4的搜索路径.

2-3-4树-查找

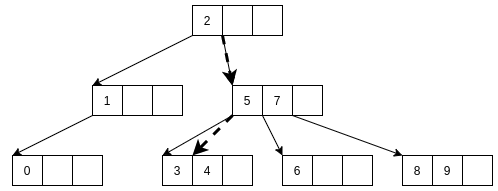
插入

对2-3-4树的插入操作需要分类讨论, 根据不同的情况需要做对应对调整, 使插入后的树依然保持平衡.

插入结点是不满的叶子结点

2-3-4树-直接插入

对插入结点是不满的叶子结点的情况, 和查找元素类似, 根据大小关系找到被插入元素在树中的位置, 因为结点没有插入满, 所以元素可以直接插入.

插入结点是满的叶子结点

2-3-4树-插入满叶子结点

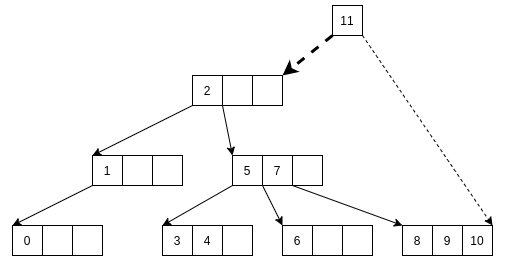
如果发现插入的结点是满叶子结点, 则需要进行调整.

首先, A元素不动.

调整B元素

我们仅截取需要调整对那颗子树.

2-3-4树-调整B元素

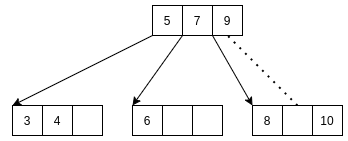
将B元素插入到父结点;

调整C元素

2-3-4树-调整C元素

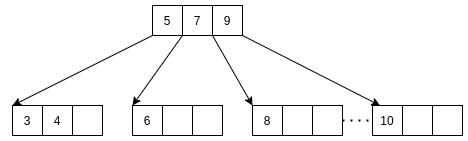
新建一个被调整结点对兄弟结点. 将C元素插入兄弟结点.

所以, 最终的插入结果是

2-3-4树-插入后

插入结点是满的非叶子结点

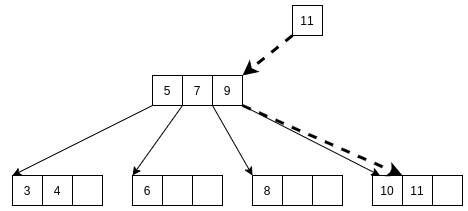
2-3-4树-插入满非叶子结点

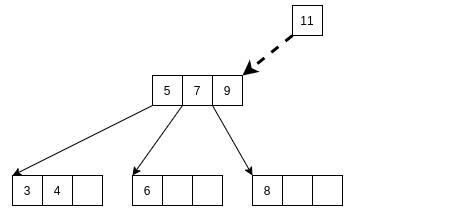
如果发现插入的结点是满非叶子结点, 情况稍微复杂一点, 需要考虑被调整结点的子结点.

同样, A元素不动.

调整B元素

2-3-4树-调整B元素

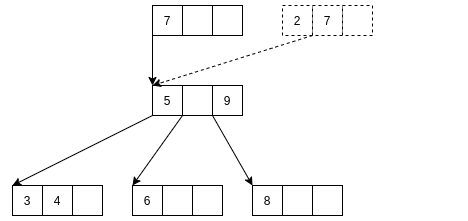
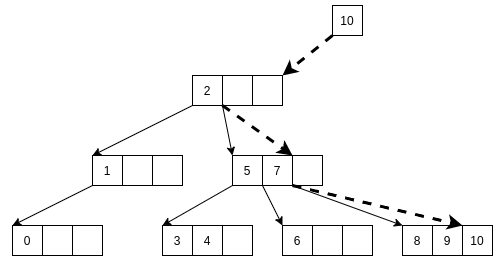
如果被调整结点没有父结点, 则新建一个父结点, 将B元素插入父结点.(也就是说, 被调整结点是根结点.)

如果被调整结点有父结点, 则将B元素插入父结点.

调整C元素

2-3-4树-调整C元素

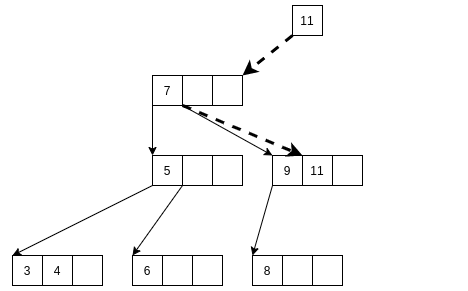
新建一个被调整结点对兄弟结点. 将C元素插入兄弟结点.

同时, 将c, d也插入到兄弟结点.(这个可以理解为C带着他的左右孩子一起插入到兄弟结点, A带着他的左右孩子一起留在原来的结点)

总结:直接插入和结点分裂

总结一下上面的操作, 其是就分为两种: 直接插入和分裂后插入

直接插入

在元素插入的结点不满的时候, 可以使用直接插入操作, 这里就不再赘述.

2-3-4树-直接插入

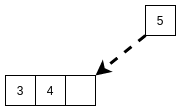
元素5直接插入到4的右边.

结点分裂

在元素插入的结点满的时候, 需要进行结点分裂操作. 简单来说, 就是将中间元素放到父结点, 如果没有父结点则新建父结点, 然后将右元素及其孩子分裂出去, 作为当前结点的兄弟结点.

2-3-4树-分裂

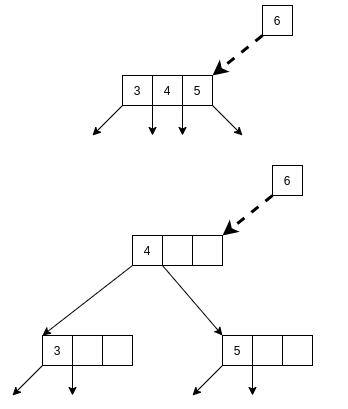
元素6在结点分裂后插入到5的右边.

可以认为, a和b是A的孩子, c和d是C的孩子, 所以A和C移动时, 需要带上自己的孩子.

删除

被删除的元素在非叶子结点

  1. 找到被删除元素的位置, 标记为D
  2. 中序遍历D
  3. 用D的中序遍历的后继元素D'替换D, 将D'作为被删除元素D
  4. 如果D在叶子结点, 则退出, 否则回到2

2-3-4树-删除非叶子结点

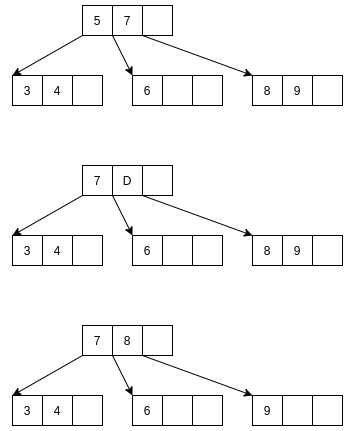
如上, 我们要删除元素5, 则先找到元素5, 然后中序遍历, 5的后继元素是7, 则用7替换5;

再将7的位置标记为待删除元素, 中序遍历之, 其后继元素是8, 所以用8替换, 且8在叶子结点, 则退出;

被删除元素在叶子结点

被删除元素在叶子结点且不是2结点

因为没有孩子了, 所以此时直接删除即可.

被删除元素在叶子结点且是2结点

如果直接删除, 会让整颗树看起来缺了一块, 按照以下操作:

  1. 删除该元素
  2. 如果兄弟结点不是2结点, 则父结点中的一个元素下移到该结点, 兄弟结点的一个元素上移到父结点, 退出
  3. 如果兄弟结点是2结点且父结点是3或4结点, 则兄弟的元素与父结点合并(实际上是作为插入操作, 插入父结点), 退出
  4. 如果兄弟结点是2结点且父结点是2结点, 则兄弟结点的元素与父结点合并, 形成3结点, 并将该结点作为考察结点, 回到2

以下:

  1. 删除元素6, 则按照规则2
    2-3-4树-删除-1

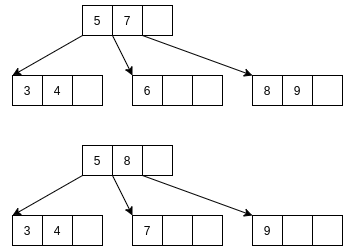
  2. 删除元素6, 则按照规则3, 按照插入操作, 父结点满了, 再插入元素3, 此时需要分裂
    2-3-4树-删除-2

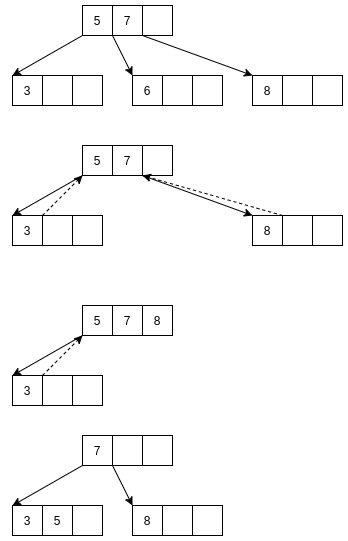
  3. 删除元素6, 则按照规则4, 如果还没有结束, 则重复2-3-4
    2-3-4树-删除-3

2-3-4树为什么可以保持平衡

根据2-3-4树的插入操作不难看出, 2-3-4树是按照向上(生成/插入父结点)和向左(生成兄弟结点)扩展的, 所以插入操作不会导致2-3-4树出现某颗子树特别高的情况.
从删除操作看, 删除某个元素之后会尽量不齐, 无法不齐的情况, 则考虑先父亲迭代(减少层数), 总之其目的是尽量保证叶子层是平的, 没有坑坑洼洼.

posted @ 2021-03-17 10:15  caibingcheng  阅读(231)  评论(0)  编辑  收藏  举报