数据结构与算法之二叉查找树
数据结构与算法之二叉查找树
原文来自个人博客(求访问/关注/收藏): https://bbing.com.cn/ CNBLOG个人博客不定期转载
什么是二叉查找树
对一般容器的查找, 我们可以按顺序遍历, 找到符合要求的元素就返回; 对于元素是有序的容器, 可以使用二分查找等方法查找, 减少操作的时间复杂度.
容易知道, 一般查找的平均时间复杂度是O(n), 二分查找的平均时间复杂度是O(logn).
什么是二叉查找树?
根结点的左子树的结点都小(大)于根结点, 根结点的右子树的结点都大(小)于根结点;
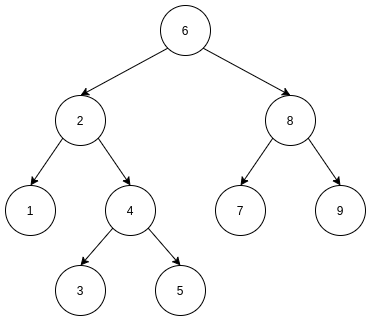
你也可能听过二叉排序树, 二叉排序树就是二叉查找树, 名字不同罢了.
二叉查找树是怎么排序的呢? 我们可以想象一颗二叉查找树, 最左边的结点最小, 最右边的结点最大, 对每个子树这个结论也成立. 所以,
二叉查找树的中序遍历就是排序操作.
如上二叉查找树, 中序遍历的结果是
1, 2, 3, 4, 5, 6, 7, 8, 9
二叉查找树的查找操作
根据二叉查找树的定义, 左子树的结点都小于根结点, 右子树的结点都大于根结点.
对于输入待查找的一个结点, 我们可以先与根结点比较, 如果小于, 则继续递归左子树, 如果大于, 则继续递归右子树, 直到找到匹配的结点.
NodeTree *bsearch(NodeTree *root, const int &val)
{
if (!root)
{
return nullptr;
}
if (val == root->val)
{
return root;
}
if (val < root->val)
{
return bsearch(root->left, val);
}
if (val > root->val)
{
return bsearch(root->right, val);
}
}
二叉查找树的插入操作
构建一颗二叉查找树也就是不停地执行二叉查找树的插入操作, 要保证插入之后的二叉树还是二叉查找树.
二叉树的插入操作就是其查找操作的进阶版本.
对需要插入的元素, 与根结点比较, 如果小于则对左子树递归, 如果大于则对右子树递归, 直到最终的叶子结点;
如果比叶子结点小, 则作为叶子结点的左子结点, 如果比叶子结点大, 则作为叶子结点的右子结点.
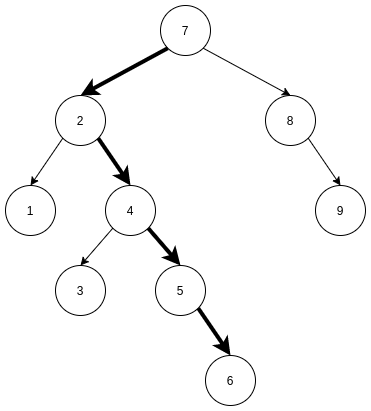
比如说插入元素6, 则按照加粗标记的箭头插入. 最终遍历到结点5时, 发现是叶子结点, 且6比5大, 则6作为5的右子结点插入.
二叉查找树的删除操作
对二叉查找树的删除可以分类讨论.
对于没有子结点和只有一个子结点的删除操作, 可以参考这个图
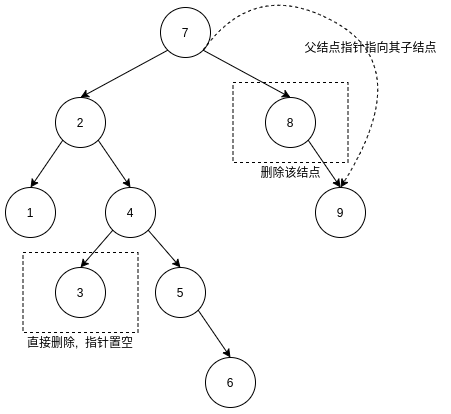
删除的结点没有子结点
如果被删除的结点没有子结点, 即是叶子结点, 则直接将叶子结点的父结点指向该叶子结点的指针置空就行.
伪代码如下:
node->parent->left == node ? (node->parent->left = nullptr) : (node->parent->right = nullptr);
delete node;
删除的结点只有一个子结点
如果被删除的结点只有一个子结点, 则将该结点的父结点指向该结点的指针重新指向该结点的子结点即可.
伪代码如下:
node->parent->left == node ? (node->parent->left = node->left) : (node->parent->right = node->right);
delete node;
删除的结点有两个子结点
如果被删除的结点有两个子结点, 则情况稍微复杂一点, 我们可以看一个特例, 被删除的结点是根结点. (不是根结点也是子树的根结点)
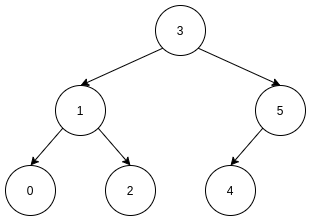
我们需要删除结点3, 怎么操作?
根据二叉查找树的定义, 我们可以知道:
- 二叉查找树的最左边结点是最小的结点;
- 二叉查找树的最右边结点是最大的结点;
所以, 又有下面两个结论:
- 左子树的最右边结点是左子树的最大结点;
- 右子树的最左边结点是右子树的最小结点;
所以, 我们有两种方案删除有两个子结点的结点;
- 用左子树的最右边结点替换被删除结点, 这时候被替换的结点依然满足左子树的结点都小于它, 右子树的结点都大于它;
- 用右子树的最左边结点替换被删除结点, 这时候被替换的结点依然满足左子树的结点都小于它, 右子树的结点都大于它;
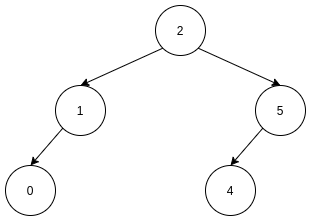
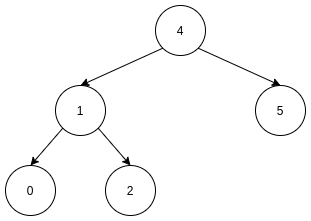
所以伪代码可以是:
bool is_rl = false; //判断是否是左子树根结点
Nodetree *rl_node = node->right; //右子树
while (rl_node->left) //右子树最左边
{
is_rl = true;
rl_node = rl_node->left;
}
rl_node->left = node->left;
if (is_rl)
{
rl_node->right = node->right;
rl_node->parent->left = nullptr;
}
delete node;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号