神经网络量化--从早期的量化算法谈起
本文首发于公众号
之前写过一系列网络量化相关的文章，它们都出自 Google 在 2018 年发表的一篇论文，目前也是 tflite 和 pytorch 等框架中通用的量化标准。不过，最近有读者在后台问我，说他看到的一些论文和我文章中的方法差别很大，被搞懵了。因此，今天想整理一下网络量化的发展脉络，帮助刚入门的同学更好地理清这里面的来龙去脉。
为什么要模型量化
关于模型量化，最直接的想法当然是把所有浮点运算都转变为定点运算，换言之需要把所有数值从 float 等浮点型上转变为 int16、int8 等整型变量，甚至变成 2bit、3bit 等极低比特表达。要知道一个 float32 的数值需要占据 4 个字节，而 int8 最多一个，不仅内存读取上快了几倍，而且定点运算也会比浮点运算更容易实现硬件加速 (2bit 等极端情况甚至用移位来实现，快到飞起)。
而神经网络里面的数值主要分三种：网络权重、中间的输出特征 (feature map)，梯度。如果把权重和特征可以定点化，那推理的时候就可以在 FPGA 等硬件上跑完整个网络，节能又高效，如果梯度也能定点化，那训练的时候也可以提速，总之，量化高效节能环保，好处大大的有。
稳扎稳打派
最开始的时候人们并不知道量化会对网络产生什么影响，因此需要一点点尝试。比如过，先对权重 weight 做量化，看看网络还能不能 work。
典型代表如 MIT 的韩松教授。刚入门模型量化的同学应该都读过他的 Deep Compression 论文，这是集剪枝量化等技术于一身的作品。其中，量化这一步的基本操作如图中所示：
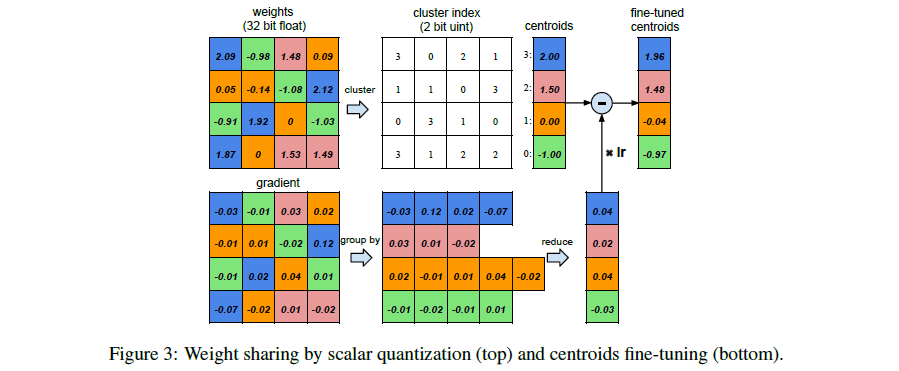
这是一种非常朴素的思想。假设权重的数值是在区间 [-1.08, 2.12] 之间，那一种最简单的量化方法就是找出 -1, 0, 1, 2 这几个整数作为中心，然后把各个权重四舍五入到这几个数即可。这种四舍五入的操作会导致误差 (这也是量化误差的来源)，假设有一个输入是 0.5，对应的浮点权重本来是 2.09，结果被我们量化到 2，在前向传播的时候，就会从 \(0.5 \times 2.09\) 变成 \(0.5 \times 2\)。综合起来，每一层前向传播都会累积大量的误差，这些误差会在 loss 上体现出来，又以梯度的形式传回来，最终，更新到原来的浮点权重上。
这种量化的思路相信大部分人都能理解。作为量化上开荒时代的作品，它对落地并不友好 (这种聚类找量化中心的形式不方便硬件加速，同时由于没有对中间的 feature 量化，前向传播其实还是要浮点进行)，并且在量化训练上也存在一些难点 (万一权重都在 0～1 之间，那量化后的权重就变成 0 或者 1，信息都丢掉了)。
之后也有一些论文针对它做了一些改进，比如周教授在英特尔做的 Incremental Network Quantization，他们采用的是移位量化，因此会量化到 \(2^{-1}\)、\(2^{-2}\) 等一些数值上 (在硬件上可以通过 bitshift 来实现，非常快，不过本质上和量化到 1、2......等意义是一样的)。他们估计是发现之前的方法在量化训练上存在一些问题 (比如直接四舍五入后，在前向传播中信息丢失太多，导致网络的训练优化很困难)，因此改进了量化训练方式，采用逐步量化，而不是一口吃成一个胖子，让一部分权重保持全精度来更好地学习量化误差。
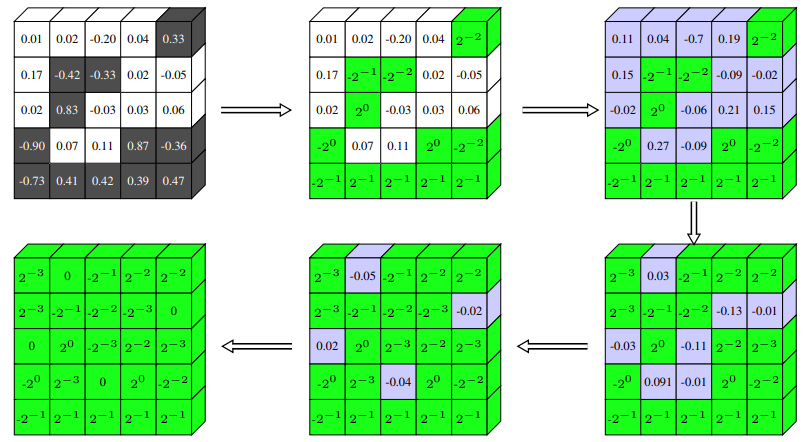
当然，这些改进工作并没有做到真正的全量化，对网络中间的 feature 还是采用浮点的形式保存 (为什么都没有对 feature 做量化，可以猜测是网络优化的难度太大)，因此落地价值都不算大。
极致压缩派
江湖上其实还有另一伙狂人，追求极致压缩，要用 3 个比特甚至 2 个比特来实现量化。
第一个吃螃蟹的人中，典型的如 Bengio 大佬。他的研究组提出了 Binarized Neural Networks，仅使用 +1 和 -1 来表达所有数值，并且是做到 weight 和 feature 都量化，因此很适合硬件部署 (如果模型效果不掉的话)。他们的量化方式也很直接，直接根据原数值判断，如果大于 0 就量化到 +1，否则量化量化到 -1。
他们量化训练的方法已经有后来 tflite 中量化训练的影子了：
- 前向传播：逐层对 weight 和 feature 进行二值化，一直到最后一层的输出；
- 反向传播：根据网络输出结果，计算 loss，回传梯度。这里需要注意，如果只是对 weight 做量化，梯度是可以正常算的 (因为梯度是对 feature 求导)，如果对 feature 也做了量化，考虑到量化本身不可导或者导数为 0，就需要使用 STE(straight-through estimator) 将梯度跳过量化函数；
- 参数更新：在浮点 weight 上更新梯度。
应该说，这套量化策略对落地是很友好的，量化训练本身也 make sense，很容易用现有的深度学习框架实现。不过，在模型效果方面，精度损失有点惨不忍睹，离全精度模型的性能相差甚大，因此不太可能落地。
后来有很多人看到这里面的潜力，纷纷涌上去一通改造。比如被各大自媒体吹捧的 XNOR-Net、Ternary weight networks、DoReFa-Net 等都对其进行较大改进，一方面对网络优化方面的难点做了些优化，另一方面也对量化策略本身做一些改进 (毕竟只量化到 -1 和 1 的话，整个网络的权重和 feature 都变成二维码了，信息损失很大)。
工业落地派
在量化领域，学术界和工业界一直存在较大的隔阂。学术界的人追求理论上的完备，并要求尽可能低的压缩比特 (8bit 是 baseline，没什么难度，不做到 4bit 以下发什么论文)，但工业界需要的是能落地的方案，所谓落地，就是硬件上能很快跑起来，同时精度要没什么损失，至于什么 2bit、3bit，要么精度没法看，要么需要特殊的硬件加持，工程师们提不起兴趣。
因此，以 Google 为代表的企业提出了一套更加通用的量化标准，并且在 tflite 中真正实现落地。这套标准就是我前面文章中介绍的量化算法，对应论文《Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference》。
这篇文章相比前面介绍的那些，优点在于它考虑到更加现实的落地需求，针对 8bit 这样的量化要求提出了一套更加有效的量化策略，尽可能保证精度，保证落地的效果 (毕竟大家更多的还是需要在 8bit 上把精度做到最高)。
回顾一下，这篇论文提出的量化策略是把浮点权重和 feature 通过线性映射量化到 [0, 255] 的区间 (对于 8bit 来说)。我们重点对比一下在前向传播时和之前文章的区别 (由于是全量化流程，因此只对比 Bengio 的 BNN 网络)。
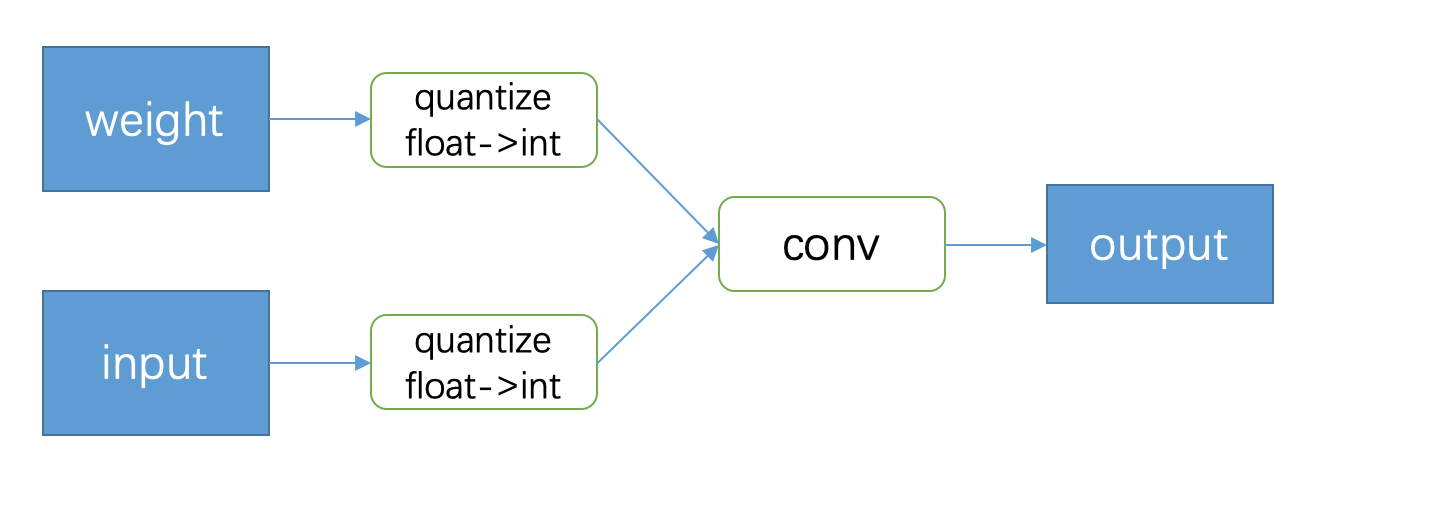
上图就是 BNN 前向传播的基本思路。正如前文介绍的，BNN 其实就是把 input 和 weight 分别量化后，再做卷积或者其他运算，得到的 output 也同样是量化的，这个 output 会继续和后面的量化 weight 进行下一步操作。
而 Google 的文章相比而言，在 output 的地方多了一些额外的操作：
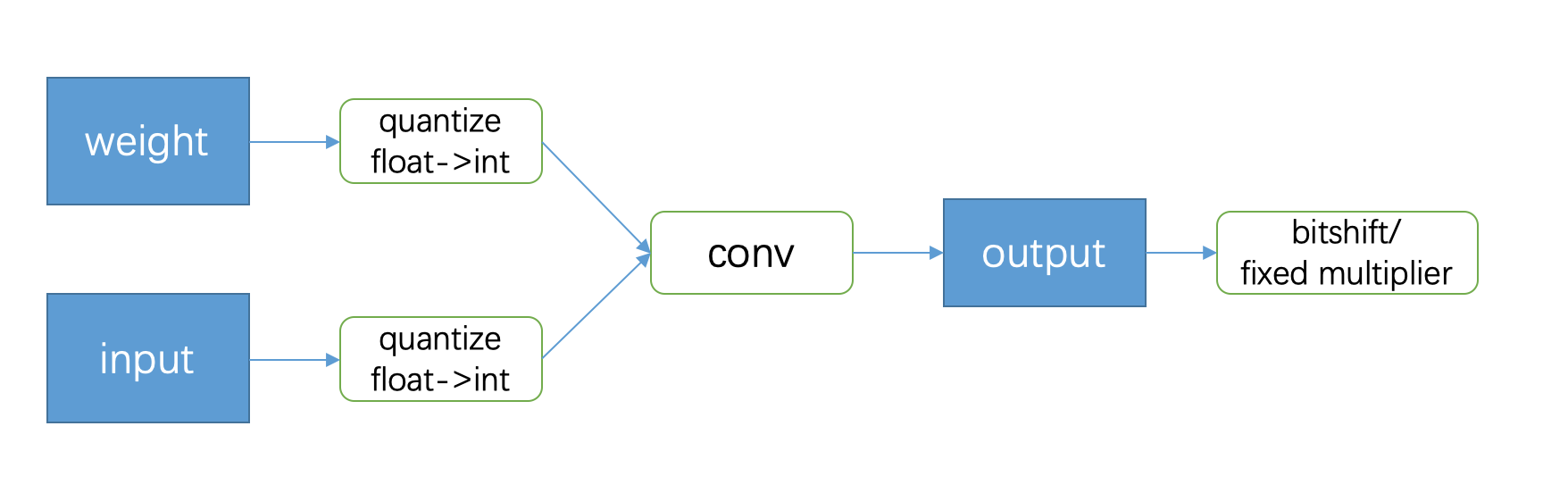
上图是 Google 论文里面卷积在量化推理时的流程 (不熟悉的同学请查阅我之前的文章)。可以看到，和 BNN 最主要的差异其实是在 output 的时候会有一个 bitshift 并乘上一个定点小数「fixed multiplier」。为什么要多这一步呢？
我的理解是这样的，量化其实是把 weight 和 input 从浮点这个 domain 转换到另一个 domain (int8，或者 2bit 等)。在 BNN 网络中，每一层的 output 受 weight 和 input 的影响，也从浮点域被转换到定点域，然后这个 output 作为下一层的 input 继续影响下一层的数值分布 (或者叫概率分布)，如此下去，就导致整个网络的输出和原先浮点输出相比差了十万八千里。但是，在参数更新的时候，又是在浮点权重上更新的，对于复杂网络来说，优化上难度极大。
而 Google 的工程师们在 output 后面接了一个 bitshift + fixed multiplier 的操作，其实是把每一层量化的输出和原先的浮点结果保持在一个可控的线性映射上 (看过我之前的文章的话，你就会明白，这里面每一层量化的输出和原来的浮点输出相比，都可以通过一个 scale 和 zeropoint 进行换算)。由于每一层的量化结果都只是浮点结果的线性映射，因此整个网络的输出结果在概率分布上和原先的浮点运算结果相差不会很大，对网络优化和性能的保持有很大作用。
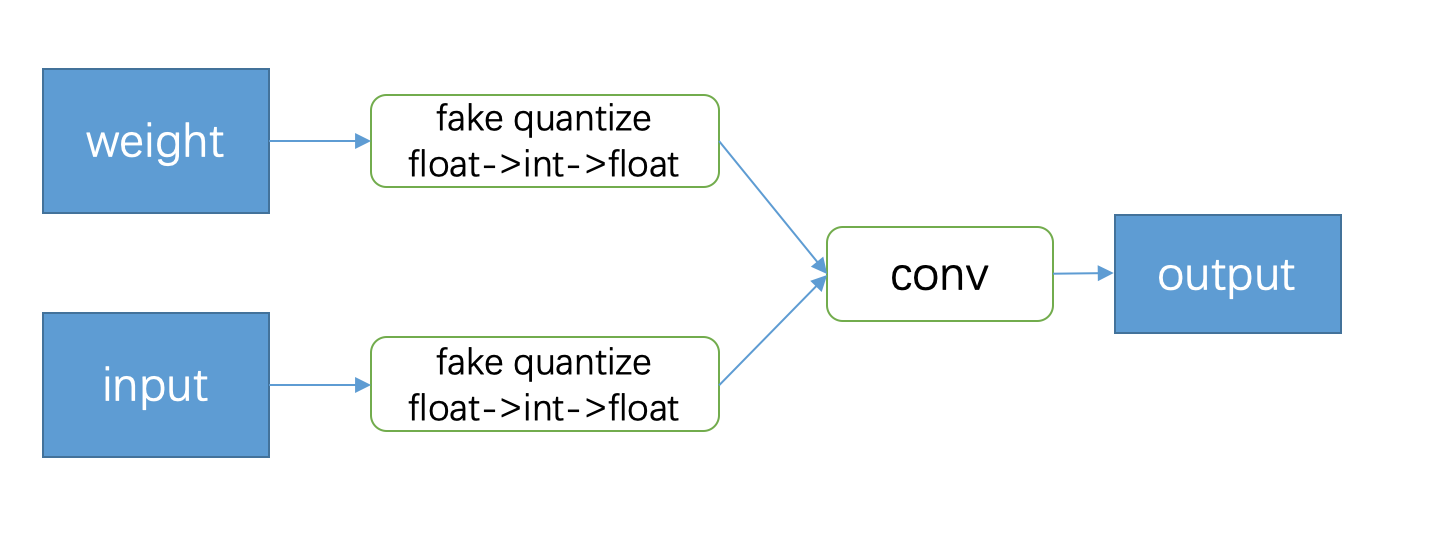
除此以外，很多同学对 Google 在量化训练时采用的伪量化 (论文称 simulated training，tflite 里面叫做 fake quantize，如下图所示) 表示不理解。其实这一步也是为了让网络的优化更加简单。细想一下，按照 Google 给出的量化推理步骤，这里面从浮点到定点的转换中，误差主要来自量化函数 (round) 的数值截断以及后面的 bitshift + fixed multiplier，其中，又以截断误差最为严重。因此，我们就在量化训练的前向传播中加上这一步 (即 fake quantize 中 float->int 这一步)。
那为什么又要反量化回 float 呢？这不是多此一举？我在之前的文章中提到过 Google 论文里的一个公式：
这其实是 Google 量化方案的总纲领。这里面的 \(q_1\)、\(q_2\)、\(q_3\) 分别是量化后的 input、weight、output，通过 \(S\) 和 \(Z\) 可以换算回对应的浮点数。而反量化就是为了保证量化训练的时候，得到的 output 可以对应这里的 \(S_3(q_3^{i,k}-Z_3)\)。这和前面说的 bitshift + fixed multiplier 是呼应的。前者保持数值在浮点域 (方便量化训练)，后者保持数值在定点域，而彼此之间可以通过 \(S\) 和 \(Z\) 换算得到。这也是这篇文章区别于 BNN 的地方。
当然，如果量化到 2bit 或者 3bit 等极端情况，这种量化训练的方法也会存在很大困难，但工业界也不追求这种极端的量化，只要保证 int8 的效果能赶上全精度网络就行。
这里要多说一句，在大部分量化训练框架中，如果在 python 里面对网络进行量化，那么一般对应的是训练时的伪量化，换句话说，并不是真正意义上的量化。一般需要用 C/C++ 等更底层的语言部署到 DSP/FPGA 等硬件上面运行，才能得到真正的量化效果 (包括速度和精度)。伪量化的精度一般会略微高于真实量化，原因在于伪量化只模拟了截断带来的损失，但其实 bitshift + fixed multiplier 这一步也会有一点损失，加上底层代码在实现上和前端的 python 代码可能会存在一些差异，导致实际部署的时候，量化效果会稍差于伪量化的效果 (在一些底层视觉任务中尤其明显，比如图像修复等)。
后量化时代
Google 这一套量化方案成了工业界事实上的量化标准 (毕竟人家在 tflite 中抢先一步落地了，所以很多厂商都选择跟进，早就是优势)，后来不少公司，包括学术界的一些改进都是在这套框架下进行的。这里说的后量化时代，指的也是在 Google 这套框架下进行的各种改进研究。
按照这套量化方案的理论，只要找出网络中每一层 weight 以及 feature (叫 activation 也行) 的 scale 和 zero point，就可以将全精度的模型转换为量化的模型。因此，这套量化方案下的量化算法分两种：后训练量化 (post training quantization，简称 PTQ) 和量化感知训练 (quantization aware training，简称 QAT)。前者就是在不重新训练的前提下，直接找出 scale 和 zero point，操作起来相对方便友好 (最新的一些
算法也会修改一些网络权重，典型如高通的 DFQ)。而后者需要在网络中加入 fake quantize 节点进行量化训练，操作起来相对繁琐，但效果会更好 (一般来说，QAT 的效果决定了 PTQ 的上界)。
最后
这篇文章从早期量化算法的研究谈起，简单梳理了神经网络量化的发展脉络，并引申到目前工业界量化方案中的诸多改进点。扯了这么多，基本是我个人的一些感悟和思考，如有雷同，三生有幸，如不苟同，后台坐等撕逼。
后面的文章中，我会重点介绍一些比较有效的 PTQ 和 QAT 算法，感兴趣的读者欢迎一键三连等发车。
欢迎关注我的公众号「大白话AI」，立志用大白话讲懂AI
