图笔记
图笔记
图的遍历代码结构和回溯代码结构相似,因此在整理回溯题目之后整理了图相关的题目,这部分的题目考察较少,不建议花太多工夫,了解常用的算法即可,力扣周赛后两题极高概率考
Graph graph;
boolean[] visited;
/* 图遍历框架 */
void traverse(Graph graph, int s) {
if (visited[s]) return;
// 经过节点 s
visited[s] = true;
for (TreeNode neighbor : graph.neighbors(s))
traverse(neighbor);
// 离开节点 s
visited[s] = false;
}
可以看到,图的遍历框架中,visited[]用于防止图走环,无环图不需要visited[]
在回溯代码框架中,visited[]更新是放在for循环中的,更关注树枝
图的学习过程,应当关注两点,
- 构建图(buildGraph,必须写熟)
- 图遍历
💚 -- Easy
💛 -- Medium
🧡 -- Hard
题目顺序,codetop.cc 默认排序规则(题目少,出现的频次很少)
💛207. 课程表 --->环检测(使用visited[] 和 onPath[])
拓扑排序联想场景:课程依赖
按照二叉树去联想,先完成上层的依赖课程,才能学习下层的课程
💛210. 课程表 II--->拓扑排序(后序遍历的结果进行反转,就是拓扑排序的结果,本题需要综合环判断)
💛797. 所有可能的路径--->图遍历
Dijkstra要求不能存在负权重边,从起点
start到所有其他节点的最短路径都算出来。需要辅助类 class State{int id; int distFromStart},优先队列PQ(State.distFromStart升序)
根据 BFS 的逻辑和无权图的特点,第一次遇到某个节点所走的步数就是最短距离
第一次经过某个节点时的路径权重,不见得就是最小的
因为优先级队列自动排序的性质,每次从队列里面拿出来的都是
distFromStart值最小的,所以当你从队头拿出一个节点,如果发现这个节点就是终点end,那么distFromStart对应的值就是从start到end的最短距离。
💛743. 网络延迟时间--->Dijkstra
💛1631. 最小体力消耗路径--->Dijkstra
💛1514. 概率最大的路径--->Dijkstra
并集查询Union-Find 解决图论中「动态连通性」问题的。
💛2316. 统计无向图中无法互相到达点对数-->UF
💛130. 被围绕的区域-> UF,BFS
X💛128. 最长连续序列--->该题与最长子序列不同,可以使用HashSet、UF(不建议用)
二分图判定核心在于使用DFS和BFS遍历,使用两种颜色将所有节点染色,且相邻节点的颜色不同,DFS更为常用
生成树:含有图中所有顶点的「无环连通子图」
最小生成树:所有可能的生成树中,权重和最小的那棵
一般来说,在无向加权图中计算最小生成树
使用贪心算法保证最小权重,按边权重排序,优先使用最小权重的可用边
Kruskal 最小生成树算法,关键是要熟悉并查集算法(UF + 贪心)
给定编号从 0 到 n - 1 的 n 个结点。给定一个整数 n 和一个 edges 列表,其中 edges[i] = [ai, bi] 表示图中节点 ai 和 bi 之间存在一条无向边。
如果这些边能够形成一个合法有效的树结构,则返回 true ,否则返回 false 。
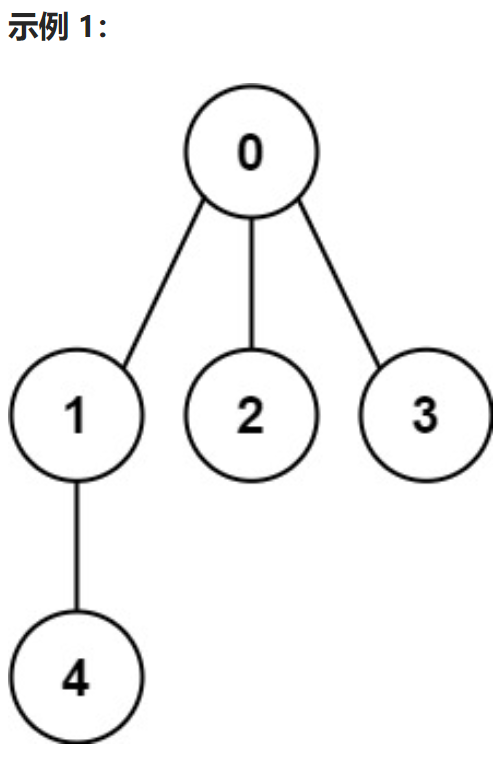
输入: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
输出: true
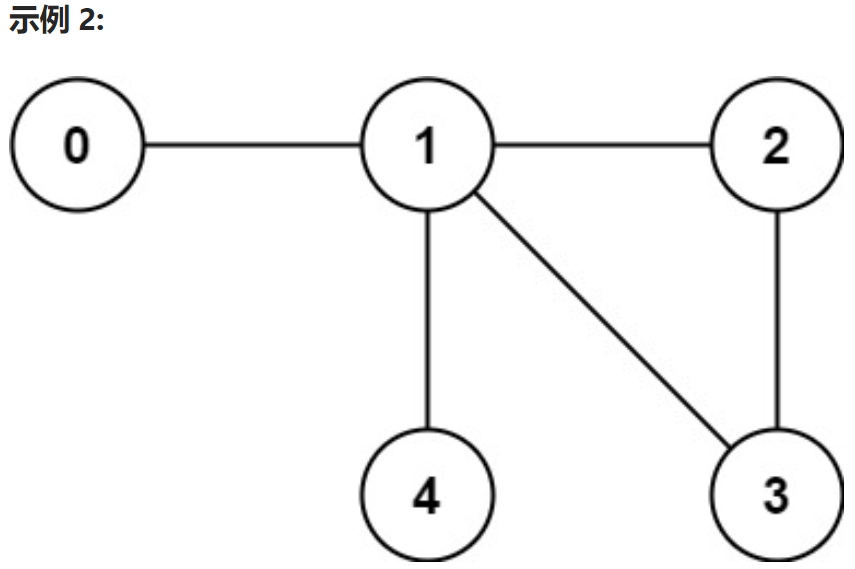
输入: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
输出: false
函数标签
class Solution {
public boolean validTree(int n, int[][] edges) {}
}
想象一下你是个城市基建规划者,地图上有 n 座城市,它们按以 1 到 n 的次序编号。
给你整数 n 和一个数组 conections,其中 connections[i] = [xi, yi, costi] 表示将城市 xi 和城市 yi 连接所要的costi(连接是双向的)。
返回连接所有城市的最低成本,每对城市之间至少有一条路径。如果无法连接所有 n 个城市,返回 -1
该 最小成本 应该是所用全部连接成本的总和。
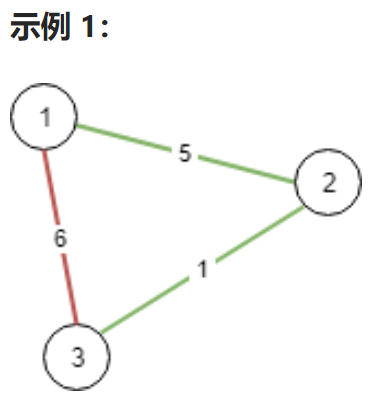
输入:n = 3, conections = [[1,2,5],[1,3,6],[2,3,1]]
输出:6
解释:选出任意 2 条边都可以连接所有城市,我们从中选取成本最小的 2 条。
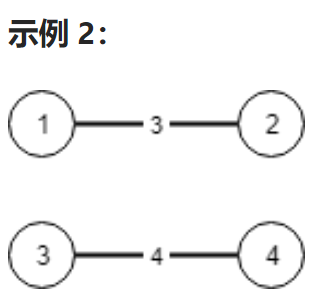
输入:n = 4, conections = [[1,2,3],[3,4,4]]
输出:-1
解释:即使连通所有的边,也无法连接所有城市。
函数标签
class Solution {
public int minimumCost(int n, int[][] connections) {}
}
💛1584. 连接所有点的最小费用--->注意记录点之间距离的技巧int[] {i, j, cost}
Prim 算法 利用「切分定理」的贪心思想,使生成树的权重尽可能小,不需要事先排序
(切分定理+BFS+visited)
「切分定理」:对于任意一种「切分」,其中权重最小的那条「横切边」一定是构成最小生成树的一条边。
不断的将相邻节点加入横切边的队伍中,依据
cut({a,b,c}) = cut({a,b}) + cut({c})BFS中,使用PriorityQueue不断将最小权边取出,添加到生成树中
适用的题目与Kruskal是一样的
需要实现的方法
class Prim {
// 核心
PriorityQueue<int[]> pq;
int weight;
boolean[] inTree;
public Prim(int n, ArrayList<int[]>[] graph) {}
void cut(int node) {}
boolean isConnected() {}
int weight() {}
}
名流算法
1、所有其他人都认识「名人」。
2、「名人」不认识任何其他人。
假设你是一个专业的狗仔,参加了一个 n 人派对,其中每个人被从 0 到 n - 1 标号。在这个派对人群当中可能存在一位 “名人”。所谓 “名人” 的定义是:其他所有 n - 1 个人都认识他/她,而他/她并不认识其他任何人。
现在你想要确认这个 “名人” 是谁,或者确定这里没有 “名人”。而你唯一能做的就是问诸如 “A 你好呀,请问你认不认识 B呀?” 的问题,以确定 A 是否认识 B。你需要在(渐近意义上)尽可能少的问题内来确定这位 “名人” 是谁(或者确定这里没有 “名人”)。
在本题中,你可以使用辅助函数 bool knows(a, b) 获取到 A 是否认识 B。请你来实现一个函数 int findCelebrity(n)。
派对最多只会有一个 “名人” 参加。若 “名人” 存在,请返回他/她的编号;若 “名人” 不存在,请返回 -1。
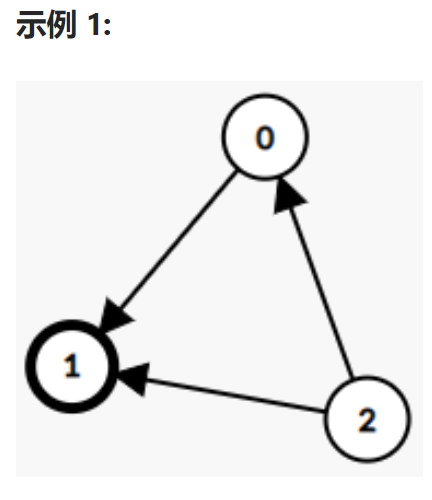
输入: graph = [
[1,1,0],
[0,1,0],
[1,1,1]
]
输出: 1
解释: 有编号分别为 0、1 和 2 的三个人。graph[i][j] = 1 代表编号为 i 的人认识编号为 j 的人,而 graph[i][j] = 0 则代表编号为 i 的人不认识编号为 j 的人。“名人” 是编号 1 的人,因为 0 和 2 均认识他/她,但 1 不认识任何人。
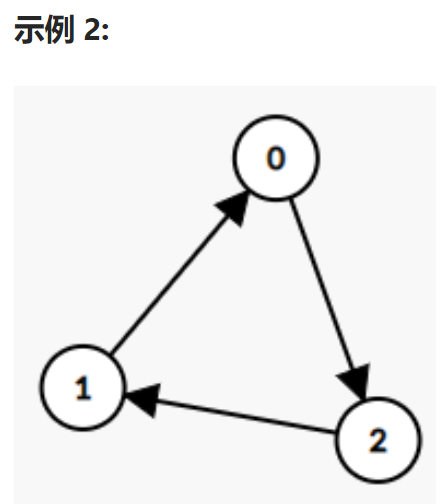
输入: graph = [
[1,0,1],
[1,1,0],
[0,1,1]
]
输出: -1
解释: 没有 “名人”
函数标签
/* The knows API is defined in the parent class Relation.
boolean knows(int a, int b); */
public class Solution extends Relation {
public int findCelebrity(int n) {}
}

