My blog in AI -- 梯度下降算法

人工神经网络是对生物神经网络的模仿，神经网络对一个问题的学习，需要经历数据输入、网络参数的训练、超参数的调节等部分。

这次我们来详细讨论一下神经网络的学习过程。

假设我们要训练一个神经网络去识别一张图片里面是否有一只狗，当然现阶段我们只是宽泛的讨论神经网络处理该问题的流程。

首先，我们会有一个规范化的图片集，里面包含了各种类型的图片（像素为28*28），有小狗的，没有小狗的，称为训练数据集。还有一个测试数据集，用来验证神经网络的学习情况。

然后，我们需要设计一个神经网络，用以学习这个问题。假设我们采用S型神经元，并使用如下的网络结构：

图中输入神经元有784个，因为输入的图片是28*28的。

图中有两个隐藏层和一个输出层。

假设我们训练集的大小为n，则训练输入为x1,x2,....,xn

要训练神经网络，会用一个代价函数，这个代价函数的基本形式为：

　　C（w,b）, 是权重和偏置的函数。

我们的目标就是，找到一组权重和偏置，对于所有的输入，神经网络的输出与目标输出之间的差异最小。

常见的代价函数有：

　　二次代价函数：

　　

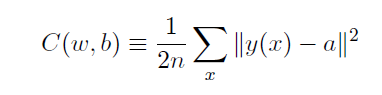
　　交叉熵代价函数：

 　　　　

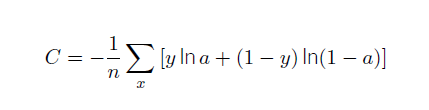
y表示对于输入x的函数，表示期望的输出。a表示输入为x时，网络的输出。

从上述两种代价函数的形式可以看出，代价函数就是用来标记网络输出与正确值之间的差异。

神经网络的训练过程正是一个寻找到最佳的权重和偏置，使得对于所有的输入与预期输出的差异最小的过程。

那么，用什么样的算法进行上述过程的计算呢？

我们知道，代价函数是权重和偏置的函数，即C（w, b）

学过高等数学的人应该都知道，对于函数的某一点，沿着梯度的反方向运动，函数的值减小的最快。

神经网络的梯度下降学习算法正是基于此，我们初始化一个权重和偏置的矩阵，然后沿着代价函数梯度的方向去改变权重和偏置，直到代价函数足够小。

 

因此，我们通过如下的规则，来更新权重和偏置，让代价函数逐步变小：

 

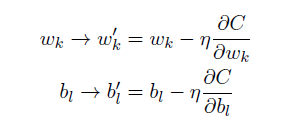
 梳理一下，神经网络的学习过程，大致如下：

1. 输入x1, 计算a,并代价函数求和中的一项，并对所有样本重复上述过程，得到代价函数C（w，b）

 2.计算所有的偏导分量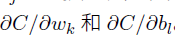

3.更新权重和偏置，重复上述过程。

从上述过程中，可以看出，如果样本量很大的话，权重和偏置更新的速度就会非常的慢，学习的效率就会变低。

因此，在生产中，一般都会把样本随机的分成一个一个的小批量数据，计算完一个小批量数据后就可以更新权重和偏置，这样就可以加快学习的速度，这叫随机梯度下降。