创建用于预测序列的人工智能模型，调整模型的超参数。

上一篇：《创建用于预测序列的人工智能模型（四），评估模型的能力》

序言：人工智能模型的研发过程实际上是一个多阶段的迭代过程，包括数据准备、模型架构设计、训练和验证，而超参数的调整和优化则始终贯穿其中，是提升模型性能的重要环节。

调整学习率

在前面的例子中，你可能还记得，我们使用了如下的优化器来编译模型：

model.compile(loss="mse",

optimizer=tf.keras.optimizers.SGD(lr=1e-6, momentum=0.9))

在这里，我们使用了一个学习率为 1×10−61 \times 10^{-6}1×10−6。但这个数字看起来像是随便选的。如果改变它会怎么样？我们又该如何找到最优的学习率呢？这需要大量的实验来找到最佳值。

幸运的是，tf.keras 提供了一种回调函数，可以帮助你随着时间调整学习率。在第 2 章中你学过回调函数，它会在每个 epoch 结束时被调用，比如用于在准确率达到目标时取消训练。

你也可以使用回调函数调整学习率参数，并将该参数的值与相应 epoch 的损失进行绘图，从而确定最佳的学习率。

要实现这一点，可以创建一个 tf.keras.callbacks.LearningRateScheduler，并让它填充 lr 参数的初始值。例如：

lr_schedule = tf.keras.callbacks.LearningRateScheduler(

lambda epoch: 1e-8 * 10**(epoch / 20))

在这个例子中，我们的学习率从 1e−81e^{-8}1e−8 开始，然后每个 epoch 增加一点点。当完成 100 个 epoch 时，学习率将达到大约 1e−31e^{-3}1e−3。

接下来，可以用初始学习率 1e−81e^{-8}1e−8 初始化优化器，并在 model.fit 调用中指定使用这个回调：

optimizer = tf.keras.optimizers.SGD(lr=1e-8, momentum=0.9)

model.compile(loss="mse", optimizer=optimizer)

history = model.fit(dataset, epochs=100,

callbacks=[lr_schedule], verbose=0)

通过 history = model.fit，训练历史（包括损失）会被保存下来。然后你可以用以下代码将每个 epoch 的学习率与损失绘制在一起：

lrs = 1e-8 * (10 ** (np.arange(100) / 20))

plt.semilogx(lrs, history.history["loss"])

plt.axis([1e-8, 1e-3, 0, 300])

这段代码设置了学习率值，与 lambda 函数使用的公式相同，并将其与 1e−81e^{-8}1e−8 到 1e−31e^{-3}1e−3 范围内的损失进行绘图。结果如图 10-4 所示：

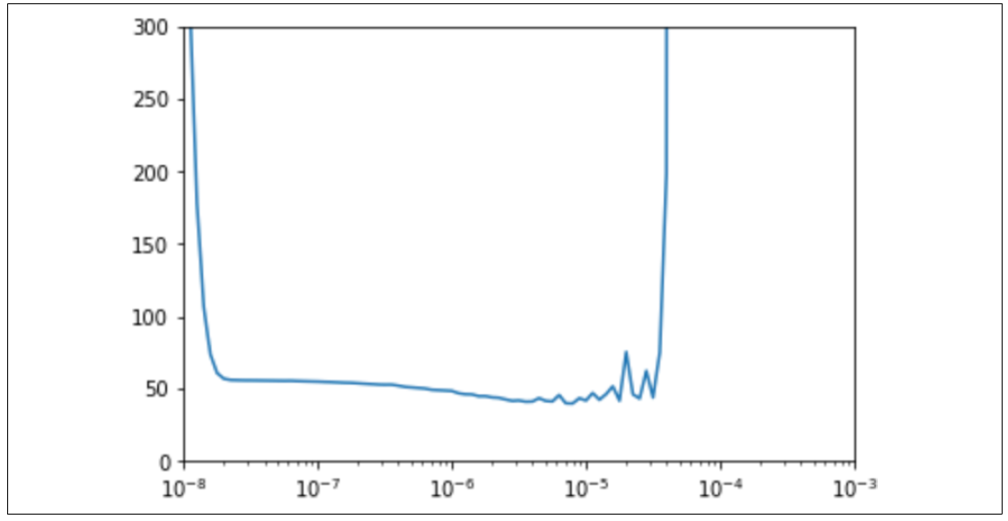
图 10-4：绘制学习率与损失的关系图

从图中可以看出，虽然之前将学习率设置为 1e−61e^{-6}1e−6，但 1e−51e^{-5}1e−5 对应的损失更小。因此，你可以重新定义模型，将学习率设置为新的值 1e−51e^{-5}1e−5。

训练模型后，你可能会发现损失有所降低。在我的例子中，学习率为 1e−61e^{-6}1e−6 时最终损失为 36.5，而学习率为 1e−51e^{-5}1e−5 时损失降低到了 32.9。然而，当我对所有数据进行预测时，结果如图 10-5 所示，预测看起来有些偏差。

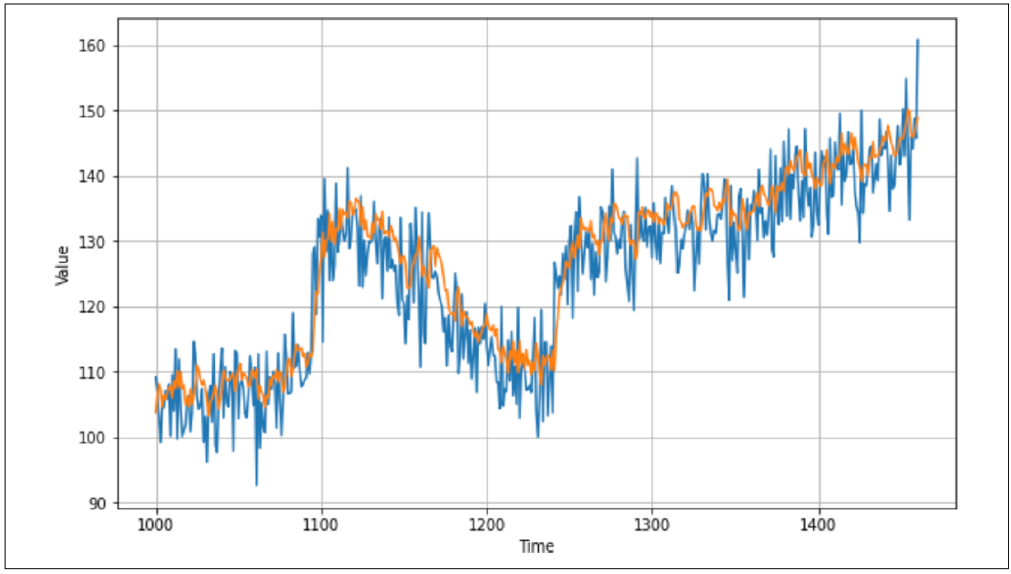
图 10-5：调整学习率后的图表

当我测量 MAE（平均绝对误差）时，结果是 4.96，比之前稍微退步了一点！

话虽如此，一旦你确定了最佳学习率，就可以开始探索其他方法来优化网络的性能了。一个简单的起点是调整窗口大小——用 20 天的数据预测 1 天的结果可能不够充分，你可以尝试使用 40 天的数据窗口。另外，也可以尝试训练更多的轮次（epochs）。通过一些实验，你可能会把 MAE 降到接近 4，这已经是个不错的结果了。

总结：优秀的人工智能研发工程师对超参数的掌握就如同驾驶技能之于司机，是一项基本却至关重要的能力。熟练调整超参数不仅能优化模型性能，还能缩短研发周期，提高解决复杂问题的效率。这种能力是人工智能开发中不可或缺的一部分，贯穿于整个模型训练和优化的迭代过程。