自学最短路算法
自学最短路算法
Coded by Jelly_Goat on 2019/4/13.
All rights reserved.
来自一个被智能推荐了一万年\(\text{【模板】单源最短路径}\)的蒟蒻小金羊。
一、floyd算法
说实话这个算法是用来求多源最短路径的算法。
但是这个时候我们可以引用一下来先做一个铺垫。
算法原理:
动态规划。
typedef long long int lli;
lli map[5001][5001];
int n;
void floyd()
{
for (register int i=1;i<=n;i++)
for (register int j=1;j<=n;j++)
for (register int k=1;k<=n;k++)
if (map[i][j]>map[i][k]+map[k][j])
map[i][j]=map[i][k]+map[k][j];
}
最后程序中的map[i][j]就是i->j的最短路径长度。
其他:
时间复杂度:\(O(n^3)\),空间复杂度:\(S(n^2)\)(用的是邻接表)。
以及如果题目中数据范围\(n\leq5000\),一般就是Floyd没跑了。
二、Bellman-Ford算法
最经典的最短路算法之一,衍生品(其实主要就是SPFA)简直不可胜数。
但是我们现在还是先回到这个算法本身。
算法原理:
我们用一个结构体存一下边。注意,这个时候链式前向星还没有用到。
struct edge{
int from,to;
lli dis;
edge(){
from=to=dis=0;
}
}Edge[500001];
通俗易懂的变量名字
然后就可以进行比较宽泛的“松弛”操作。
“松弛”是什么?就是我们利用三角形不等式的方法逼近更新最短路。
这就是这个算法的核心。
为什么这个算法是对的?
不行,我不证明
我们从一个点出发,必定会更新到其他节点。再从其他节点更新其他节点,必定会得到其他节点的松弛操作。
因为我们每一个节点都松弛了边数遍,所以松弛必定会得到其他节点的最短路(距离源点)。
所以这个算法是正确的。
但是这个不是严谨的证明,证明还是要上网右转百度。
代码实现?
struct edge
{
int from, to;
lli dis;
edge()
{
from = to = dis = 0;
}
} Edge[500001];
lli dis[10001];
int nodenum, edgenum, origin_node, querynum;
bool Bellman_Ford()
{
dis[origin_node] = 0;
//核心:松弛操作
for (int i = 1; i <= nodenum - 1; i++)
{
for (int j = 1; j <= edgenum; j++)
{
if (dis[Edge[j].to] > dis[Edge[j].from] + Edge[j].dis)
dis[Edge[j].to] = dis[Edge[j].from] + Edge[j].dis;
}
}
for (int i = 1; i <= edgenum; i++)
if (dis[Edge[i].to] > dis[Edge[i].from] + Edge[i].dis)
return false;
return true;
}
三、SPFA(Bellman-Ford算法的队列优化)
这就是上文所说的衍生物。
但是在这之前我们还得学习一下链式前向星——一种存储图的方式。
前置知识:链式前向星
我们会发现,bf之所以跑得慢,就是因为对于边的更新次数太多了!所以我们想要像搜索那样更新每一个节点。
但是我们会发现,我们只需要一个节点的所有出边就够了。
这样存图有什么好处?
对于空间上:对比邻接矩阵,我们会发现我们如果存储有向边的话,矩阵的空间损耗太大,而且二位数组容易爆。
对于时间上:O(1)访问某一个节点的第一个出边。
那么怎么实现?
首先我们需要开一个节点个数大小的数组head[10001],用来存储每一个节点的“第一条”出边,然后加上一个变量cnt用来转移下标。
然后我们需要在结构体内部做修改——改成一个“出边”:出边的终点、出边的长度、下一条出边这三项就可以了。
struct edge{
int to,next;
lli dis;
edge(){
to=next=dis=0;
}
}Edge[500001];
int cnt=1;//存储的实际上是下一条边的下标
然后我们进行添加边的操作。
inline void add_edge(int from,int to,lli dis)
{
Edge[cnt].to=to;//先给要添加的边进行一个赋值
Edge[cnt].dis=dis;
//重点理解:连接到上一条from的出边
Edge[cnt].next=head[from];
//将head[from]——from的最后一条出边改成这个边,然后到下一条边的下标(下标++)
head[from]=cnt++;
}
看起来就很简单
上面说:head[10001]`,用来存储每一个节点的“第一条”出边
实际上是最后一条出边,但是我们遍历所有出边的时候哪管那个是头上的边......
我们对这个算法进行一个测试,看看到底正确性如何。剪贴板子
然后进入正题——
SPFA算法原理:
引自GGBeng大佬的blog:原文(P.S:解释的我觉得还不错)
我们学过了Bellman-Ford算法,现在又要提出这个SPFA算法,为什么呢?
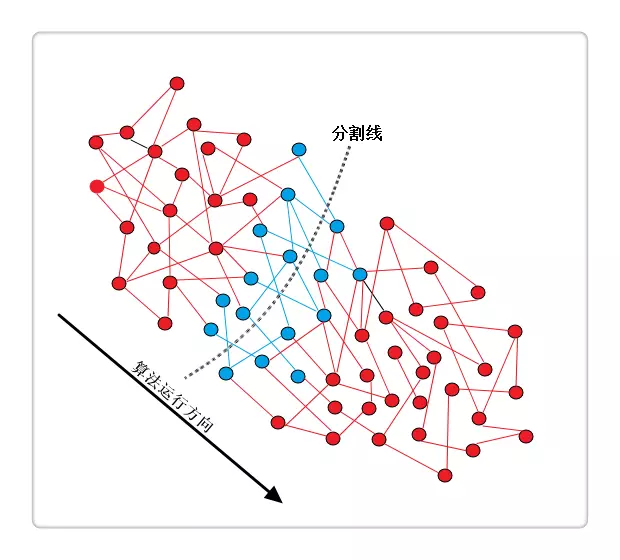
考虑一个随机图(点和边随机生成),除了已确定最短路的顶点与尚未确定最短路的顶点之间的边,其它的边所做的都是无用的,大致描述为下图(分割线以左为已确定最短路的顶点):
其中红色部分为所做无用的边,蓝色部分为实际有用的边。既然只需用到中间蓝色部分的边,那就是SPFA算法的优势之处了。
就是因为我们要舍弃没有用的边的遍历,我们引进了SPFA的思想。
首先先给一个全局定义:
#include <iostream>
#include <cstdio>
#include <bitset>
#include <queue>
#include <cstring>
using namespace std;
typedef long long int lli;
const lli oo = 2147483647LL, INF = oo;
struct edge
{
int to, next;
lli dis;
edge()
{
to = next = 0, dis = oo;
}
} Edge[500001];
int nodenum, edgenum, origin_node, end_node, cnt = 1;
int dis[10001], head[400001];
bitset<10005> vst; //bool vst[10005];
queue<int> q;
然后我们需要进行SPFA!
1.BFS版本
BFS?听起来挺熟悉......
然而还真的是借用了这个思想。
队列里面要放需要扩展的节点,然后还要用vst[]表示是否在队列中。
对于每一个取出来的节点,我们扩展所有的出边的终点,我们发现可以进行判断&松弛——没错,还是那个松弛。
如果在队列中,就不需要重复加入队列。
但是如果每一个节点重复加入了n次,就说明这个地方有一个可以无限松弛的负环。
#include <iostream>
#include <cstdio>
#include <cctype>
#include <bitset>
#include <queue>
#include <cstring>
using namespace std;
typedef long long int lli;
const lli oo = 2147483647LL, INF = oo;
struct edge
{
int to, next;
lli dis;
edge()
{
to = next = 0, dis = oo;
}
} Edge[500001];
int nodenum, edgenum, origin_node, end_node, cnt = 1;
int dis[10001], head[400001], cnt2[10001];
bitset<10005> vst; //bool vst[10005];
queue<int> q;
//quick input of num
template <typename T_>
inline T_ getnum();
inline void add_edge(int from, int to, lli dis)
{
Edge[cnt].dis = dis;
Edge[cnt].to = to;
Edge[cnt].next = head[from];
head[from] = cnt++;
}
bool spfa()
{
q.push(origin_node);
vst[origin_node] = true;
dis[origin_node] = 0;
while (!q.empty())
{
int t = q.front();
q.pop();
vst[t] = false;
for (register int i = head[t]; i != 0; i = Edge[i].next)
{
int to = Edge[i].to;
if (dis[to] > dis[t] + Edge[i].dis)
{
dis[to] = dis[t] + Edge[i].dis;
if (!vst[to])
{
q.push(to);
vst[to] = true;
if (++cnt2[to] > nodenum)
return false;
}
}
}
}
return true;
}
int main()
{
#ifdef WIN32
freopen("in.txt", "r", stdin);
freopen("out.txt", "w+", stdout);
#endif
nodenum = getnum<int>(), edgenum = getnum<int>(), origin_node = getnum<int>();
for (register int i = 1; i <= nodenum; i++)
{
dis[i] = oo;
}
for (register int i = 1; i <= edgenum; i++)
{
int from = getnum<int>(), to = getnum<int>();
lli dis = getnum<lli>();
add_edge(from, to, dis);
}
if (!spfa())
{
cout << "Exist a minus circle." << endl;
return 0;
}
else
{
for (register int i = 1; i <= nodenum; i++)
{
printf("%d ", dis[i]);
}
}
return 0;
}
//quick input of num
template <typename T_>
inline T_ getnum()
{
T_ res = 0;
bool flag = false;
char ch = getchar();
while (!isdigit(ch))
{
flag = flag ? flag : ch == '-';
ch = getchar();
}
while (isdigit(ch))
{
res = (res << 3) + (res << 1) + ch - '0';
ch = getchar();
}
return flag ? -res : res;
}
代码如上。