选择排序算法

故事背景

假如本次考试，本学校有100个学生，对于每个学生我们记录了他的分数，现在你需要将同学们的分数，按照从高到低排名

思路excel地址：https://docs.qq.com/sheet/DU0doeGJIcmxtdUxT
 

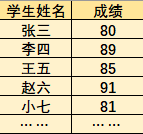
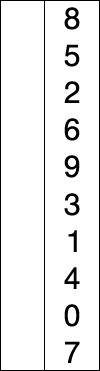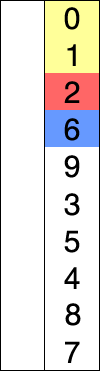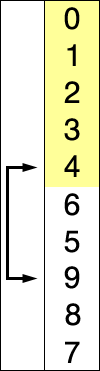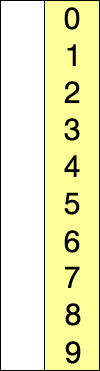
那么该如何做呢，一种办法是，遍历整个数据，然后吧分数最高的加入到一个新的列表中

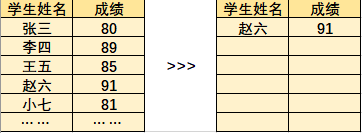
依次这样做，我们可以得到一个有序列表

从计算机的角度看待一个这个问题

O(n)时间意味着查看列表中的每个元素一次。例如，对学生列表进行简单查找时，意味着每个学生都要查看一次

要找出分数最高的学生，必须检查列表中的每个元素。正如你刚才看到的，这需要的时间为O(n)。因此对于这种时间为O(n)的操作，你需要执行n次

需要检查的元素数越来越少

随着排序的进行，每次需要检查的元素数在逐渐减少，最后一次需要检查的元素都只有一个。既然如此，运行时间怎么还是O(n2)呢？这个问题问得好，这与大O表示法中的常数相关。
后面将详细解释，这里只简单地说一说。
你说得没错，并非每次都需要检查n个元素。第一次需要检查n个元素，但随后检查的元素数依次为n  1, n – 2, …, 2和1。平均每次检查的元素数为1/2 × n，因此运行时间为O(n × 1/2 × n)。
但大O表示法省略诸如1/2这样的常数（有关这方面的完整讨论，后面我会接着讨论），

因此简单地写作O(n × n)或O(n^2)。

选择排序是一种灵巧的算法，但其速度不是很快。快速排序是一种更快的排序算法，其运行时间为O(n log n)，这将在后面介绍

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个将被移到其最终位置上，因此对 n 个元素的表进行排序总共进行至多 n -1 次交换。在所有的完全依靠交换去移动元素的排序方法中，选择排序属于非常好的一种

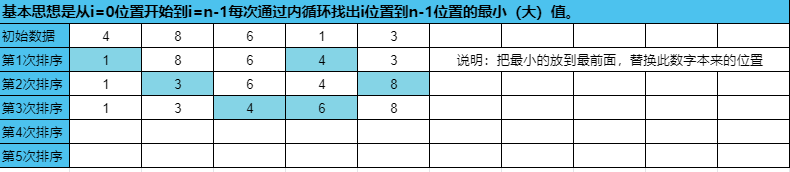
下述代码提供了类似的功能：将数组元素按从小到大的顺序排列。先编写一个用于找出数组中最小元素的函数

C 语言演示

def findSmallest(arr):
    smallest = arr[0]
    smallest_index = 0
    for i in range(1, len(arr)):
        if arr[i] < smallest:
            smallest = arr[i]
            smallest_index = i
    return smallest_index

// 现在可以使用这个函数来编写选择排序算法了。
def selectionSort(arr):
    newArr = []
    for i in range(len(arr)):
        smallest = findSmallest(arr)
        newArr.append(arr.pop(smallest))
    return newArr

// 进行测试
print selectionSort([5, 3, 6, 2, 10])

PHP 语言演示
 
<?php
$arr = array(5, 8, 6, 7, 3);
 
// 选择排序算法实现 
function SelectSort($arr = array()) {
	//获取数组长度
    $size = sizeof($arr);
	//外层循环控制比较的数值下标与轮询次数
    for ($i=0; $i<$size; $i++) {
		// 先假设最小值的位置
        $p=$i;
		//内层循环控制比较次数
        for ($j=$i+1; $j<$size; $j++) {
			// 如果 j 下标的值比 p 小标的值小
            if ($arr[$p] > $arr[$j]) {
				//记录最小值的下标
                $p = $j;
            }
        }
		// 不相同则互换位置
        if ($p != $i){
            $tmp = $arr[$i];
            $arr[$i] = $arr[$p];
            $arr[$p] = $tmp;
        }
    }
    return $arr;
}
 
// 测试运行
print_r(SelectSort($arr));

动画演示