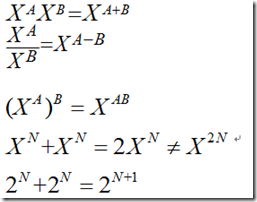数据结构与算法分析:第1、2章:引论和算法分析
第1章 引论
在看第二章算法分析之前,先来看几个数学公式:
1. 复习数学公式
1.) 指数:
2.) 对数:
3.) 级数:
那为什么需要指出上面这些数学公式呢?因为在分析算法复杂度如:T(n) = O(f(N)) 所对应的关系可能是上面这些数学公式所对应的关系,即:常量阶,线性阶,平方阶,对数阶或指数阶等。
2. 证明方法
证明数据结构分析中的结论两个最常用的方法是归纳法和反证法(证明一个定理不成立的最好方法是举出一个反倒)。
1.) 归纳法进行的证明有两个标准的部分:一是证明基准情形(base case),就是确定定理对于某个小范围内的值的正确性;二是进行归纳假设(inductive hypothesis),即假设定理对直到某个有限数k的所有情况都是成立的。然后再用这个假设定理对下一个值(通常是k+1)也是成立的,至此定理得证(在k是有限的情形下)。
2.) 反证法证明是通过假设定理不成立,然后证明该假设导致某个已知的性质不成立,从而说明假设是错误的。
3. 递归
一个函数调用用它本身时就称为递归(recursive)。如:
int F(int x)
{
if(x == 0)
return 0;
else
return 2 * F(x - 1) + x * x;
}
递归的四个基本法则:
1.) 基准情形(base case),不用递归就能求解的情形;
2.) 不断推进(making progress),递归调用必须总能朝基准情形的方向推进;
3.) 设计法则,假设所有的递归调用都能运行;
4.) 合成效益法则(compound interest rule),在求解一个问题的同一实例时,不可在不同的递归调用中做重复性的工作。
现实中的例子就是,我们查一个单词的时候,不理解对该词的解释,于是我们再去查找解释中的一些词,而对这些词的解释中的某些词又不理解,于是继续这种搜索。因为词典是有限的,所以,要么我们最终查到一处,明白此处解释中所有的单词;要么这些解释形成一个循环,无法明白其中的意思,或在解释中需要我们理解的某个单词不在这本词典里。
第2章 算法分析
算法是一个求解问题的指令集合,对于一个问题,一旦给定某种算法且确定其是正确的,那么重要的一步就是确定该算法需要多少诸如时间,空间等资源的问题。
1. 如何估计一个程序所需的时间?
1.) 如果存在正常数c和n0,使得当:
a. 如果 N >= n0时,T(N) ≤ cf(N),记作:T(N) = O(f(N)),表示T(N)的增长率小于或等于f(N)的增长率;
b. 如果 N >= n0时,T(N) ≥ cg(N),记作:T(N) = Ω(g(N)),表示T(N)的增长率大于或等于g(N)的增长率;
c. T(N) = Θ(h(N))当且仅当T(N) = O(h(N))且T(N) = Ω(h(N)),表示T(N)的增长率等于h(N)的增长率;
d. 如果 T(N) = O(p(N))且T(N) ≠ Θ(p(N)),则T(N) = o(p(N)),表示T(N)的增长率小于p(N)的增长率。
可由上面算法模型推出:
法则1:如果T1(N) = O(f(N))且T2(N) = O(g(N)),那么:
a.) T1(N) + T2(N) = max(O(f(N)), O(g(N))),两个常数级问题相加,取其中问题难度最大的值,一般用于计算一段代码中顺序语句所带来的问题难度;
b.) T1(N) * T2(N) = O(f(N) * g(N)),两个常数级问题相乘,得到两个问题难度数相乘,一般可用于循环嵌套语句所带来的问题难度
法则2:如果T(N)是一个k次多项式,则T(N) = Θ(N^k),这是个指数级
法则3:对任意常数, log^k N = O(N),它告诉我们对数增长得非常缓慢。在将常数或低阶项放进大O是非常坏的习惯,不要写成T(N) = O(2N^2)或T(N) = O(N^2+N),正确的形式是T(N) = O(N^2),低阶项一般可忽略,常数也可丢弃。此时要求的精度是很低的。
函数增长率从小到大依次为:
| 函数 | 名称 |
| c | 常数 |
| logN | 对数级 |
| log^2 N | 对数平方根 |
| N | 线性级 |
| N logN | |
| N^2 | 平方级 |
| N^3 | 立方级 |
| 2^N | 指数级 |
2.) 运行时间的计算
int sum(int n)
{
int i, partialsum;
partialsum = 0;
for (i = 1; i <= n; i++) // 占2n+2个时间单元:初始化1个时间单元,测试i <= n 占n+1个时间单元, 和对i的自增运算占n个时间单元
partialsum += i * i * i; // 占4n个时间单元:两次乘法,一次加法和一次赋值,每一个操作都是n次
return partialsum;
}
所以,以上函数总量是6n + 2,用大O表示为:O(N)。在分析问题复杂度时,我们可遵循支下法则:
法则1:for 循环,一次for循环的运行时间至多是该for 循环内语句(包括测试)的运行时间乘以迭代的次数;
法则2:嵌套的for 循环,从里向外分析这些循环,在一组嵌套循环内部的一条语句总的运行时间为该语句的运行时间乘以该级所有的for 循环的大小的乘积,如:
for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
k++;
问题难度为:O(N^2)
法则3:顺序语句,将各个语句的运行时间求和,这也意味着,其中的最大值就是所得的运行时间,如:
for (i = 0; i < n; i++)
a[i] = 0;
for (i = 0; i< n; i++)
for (j = 0; j < n; j++)
a[i] += a[j] + i + j;
上面代码有两段,第一个for 是O(N),第二个for 是O(N^2),根据法则3,这个问题的难度为O(N^2)
法则4:if/else语句,一个if/else语句的运行时间从不超过判断再加上s1和s2中运行时间长者的总运行时间:
if (condition)
s1
else
s2
递归问题难度存在好几种选择,如:
long int factorial(int n)
{
if (n <= 1)
return 1;
else
return n * factorial(n - 1);
}
上面这个问题的难度是O(N),但下面这个递归它的效率低得令人惊诧:
long int fib(int n)
{
if (n <= 1)
return 1;
else
return fib(n – 1) + fib(n - 1);
}
上面这个问题的难度将是指数级的。如果用一个for循环来实现,运行的时间将被实质性的减少下来。
2. 介绍几种算法
如何将一个问题难度最大化减小?
1.) 如果一个算法用常数时间O(1)将问题大小削减为其一部分(通常是1/2),那么该算法就是O(logN)。如果使用常数时间只是把问题减少一个常量,那么这种算法就是O(N)的。
2.) 分治(divide-and-conquer)算法,将问题分成两个大致相等的子问题,然后递归地对它们求解,这是‘分’的问题。‘治’阶段将两个子问题的解合并到一起并可能再做些少量的附加工作,最后得到整个问题的解。
3.) 二分查找(binary search)法:在一个预先已排序的整数数列A0, A1, A2, A3……A(N-1)中,查找整数X。明显的解法是从左到右扫描一遍,这样问题的大小是线性的,但却没有用到已排序的事实。二分查找法,就是验证X是否是居中的元素,如果是,一次就找到了,如果X小于居中元素,应用同样的策略在居中元素左边已排序的子序列中查找;同理如果X大于居中元素,就在居中元素右边已排序的子序列中查找。这样问题大小为log(N-1)+2,记作O(log N)。
4.) 欧几里德算法(辗转相除法)
算法通过连续计算余数直到余数为0,最后的非零余数就是最大公因数。如:1989和1950两个数,用1989/1590 的余数序列是399, 393, 6, 3, 0,得到1989和1950两数的最大公约数是3。通过上面余数序列观察到,通过两次迭代后,余数最多是原始值的一半,即问题大小为:2log N = O(log N) = O(log N)从而等到运行时间。
3. 验证算法效率
通过编写代码来实际观察运行时间与分析算法运行时间是否相匹配。当N扩大一倍时,线性程序的运行时间乘以因子2,二次程序乘以因子4,三次程序乘以因子8。如果对数程序当N增加一倍时, 其运行时间只是多加一个常数,而以O(N log N)的程序则两倍时间稍多一些。如果低阶项的系数相对地大,并且N又不是足够大时,运行时间的变化是很难观察清楚的。所以,单纯的凭运行时间区分线性程序还是O(N log N)程序是非常困难的。