数据结构：第1章 基本概念

1. 算法描述：算法是一组完成特定任务的有穷指令序列。所有的算法都必须有：输入，输出，确定性，有限性和有效性。

 

2. 选择排序(Selection Sort) 原理：首先在排序序列中找到最小元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小元素，然后放到排序列未尾。依此类推，直到所有元素均排序完毕。

复杂度分析：选择排序的交换操作介于0和(n-1)次之间；比较操作为n(n-1)/2之间；赋值操作介于0-3(n-1)次之间。
比较次数是O(n^2)，比较次数与关键字的初始化状态无关，总的比较次数N=(N-1)+(N2)+...+1 = N*(N-1)/2。交换次数为O(n)，最好情况是，已经有序，交换0次；最坏情况是，逆序，交换n-1次。交换次数比冒泡排序少多了，由于交换所需CPU时间比较所需的CPU时间多，n值较小时，选择排序比冒泡排序快。

代码如下：

#include <stdio.h>
#include <math.h>
#define MAX_SIZE 101  // 数据能存储最多元素个数
#define SWAP(x, y, t)  ((t) = (x), (x) = (y), (y) = (t))
void sort(int [], int );
int main(void)
{
    int i, n;
    int list[MAX_SIZE];
    printf("Enter the number of numbers to generate: ");
    scanf("%d", &n);
    if (n < 1 || n > MAX_SIZE)  // 如果输入的n小于1或大于数据所能存储最大数
    {
        fprintf(stderr, "Improper value of n\n");
        exit(1);
    }

    for (i = 0; i < n; i++)
    {
        // 生成n个随机数，存储在list数组中
        list[i] = rand() % 1000;
        printf("%d ", list[i]);
    }

    sort(list, n);
    printf("\nSorted array: \n");

    for(i = 0; i < n; i++)
        printf("%d ", list[i]);

    printf("\n");
}

void sort(int list[], int n)
{
    int i, j, min, temp;
    for (i = 0; i < n-1; i++)
    {
        min = i;
        for (j = i + 1; j < n; j++)
            if (list[j] < list[min])  // 如果前面元素值大于后面元素值
                min = j;
        SWAP(list[i], list[min], temp); 　// 交换数组元素值
    }
}

以上参考：http://zh.wikipedia.org/zh/%E9%80%89%E6%8B%A9%E6%8E%92%E5%BA%8F

 

3. 二分搜索法(Binary Search)[折半查找法]

对已排序的数组，再折半搜索，最坏的情况下O(log n)完成查找。基本思想：将n个元素分成个数大致相同的两半，取a[n/2]与欲查找的数x比较，如果x = a[n/2]则找到x；如果x < a[n/2]，则只要在数组a的左半部继续搜索(假设数组按升序排序)；如果x>a[n/2]，则只要在数组a的右半部继续搜索。

二分查找法应用极其广泛，而且它的思想易于理解。第一个二分搜索算法在1946年就出现了，但第一个完全正确的二分搜索算法直到1962年出现。Bentley在他的著作《Writing correct Programs》中写道，90%的计算机专家不能在2小时内写出完全正确的二分搜索算法。问题的关键在于准确地制定各次查找范围的边界以及终止条件的确定，正确地归纳奇偶数的各种情况。

用递归方式实现二分查找，需要做两件事：一是，构造递归调用终止的边界条件；二是，实现递归调用，使得每次递归调用都能向最终解逼近一步。

代码如下：

 

#define COMPARE(x, y)  (((x) < (y)) ? -1: ((x) == (y)) ? 0: 1)


int binsearch(int list[], int searchnum, int left, int right)
{
    // search list[0] <= list[1] <= ... <= list[n-1] for searchnum. Return its position if found. Otherwise return -1
    int middle;
    if (left <= rigth)
    {
        middle = (left + rigth) / 2;
        switch(COMPARE(list[middle], searchnum))
        {
            case -1: return binsearch(list, searchnum, middle + 1, right);
            case 0: middle;
            case 1: return binsearch(list, searchnum, left, middle - 1);
        }
    }
     return -1
}

 

4. 算法的性能分析

    判断标准可以包含：

    a. 程序是否能满足任务的原始规格说明；

    b. 程序是否能正确工作；

    c. 程序是否包含说明其使用方法和工作过程的文档；

    d. 程序是否有效利用函数来创建每一个逻辑单元；

    e. 程序代码的可读性如何；

    f. 程序是否有效地利用内存和外存；

    g. 程序的执行时间是否可接受

上面的f, g两条是对算法性能的评价，算法的性能会与存储空间的数量和执行所需的时间有关。

    1.) 空间复杂性包括：固定的空间需求和可变的空间需求。

        固定的空间需求：指不依赖于程序输入，输出数量和大小的空间需求，包括代码存储空间，存储简单变量，固定大小的结构变量和常量的存储空间。

        可变的空间需求：包括结构变量所需的存储空间，这些结构变量的大小依赖于所求问题的特定实例，同时还包括函数递归调用时所需的额外存储空间。

 

    2.) 时间复杂性，是指编译时间和运行时行的总和。程序的时间复杂性由程序所编写的函数所需的执行步数决定，程序步数本身是程序实例特征的一个函数，虽然一个特定实例可能具有多个特征，但程序步数的计算结果是这些实例特征的某个子集的函数。

 

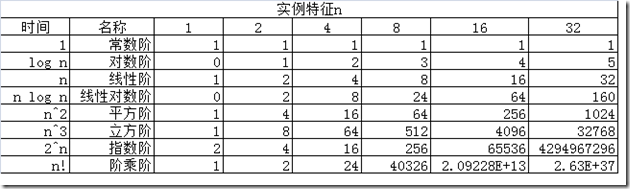
    3.) 实例特征表：

       

 

    4.) 性能测试

    使用C语言标准库中的时间事件函数进行计时测试：