1. 内存分配
三种内存分配方式：
1.) 静态数组，它要求结构长度固定，长度必须在编译时确定，这个方案最为简单且最不容易出错；
2.) 动态分配的数组，在运行时才决定数组的长度，可以分配一个新的，更大的数组，把原来数组的元素复制到新数组中，再删除原来的数组，从而达到改变数组长度的目的。决定是否采用动态数组时，需要由此增加的复杂性和随之产生的灵活性(不需要一个固定的，预先确定的长度)之间作一番权衡。
3.) 动态分配的链式结构，它提供了最大程序的灵活性，因为每个元素在需要时才单独进行分配，所以除了不能超过机器的可用内存之外，这种方式对元素的数量几乎没有限制。但链式结构的链接字段需要消耗一定的内存，在链式结构中访问一个特定元素的效率不如数组。
2. 堆栈(stack)
堆栈的数据结构特点是后进先出(Last-In First-Out，LIFO)。
1.) 堆栈接口
基本的堆栈操作通常被称为push和pop，push就是把一个新值压入到堆栈的顶部，pop就是把堆栈顶部的值移出堆栈并返回这个值。堆栈只提供对它的顶部值进行访问。我们还需要两个函数来使用堆栈，一个是检查堆栈是否为空，另一个是检查堆栈是否已满。
另一种堆栈接口提供三种基本操作：push, pop 和 top，push 操作和上面一样；pop只负责把顶部元素从堆栈中移除，不负责返回这个值；top返回顶部元素的值，但不把顶部元素从堆栈中移除。
2.) 实现堆栈
堆栈的基本方法是：被push 到堆栈时把它们存储于数组中连续的位置上，记住最后一个被push值的下标。如果需要执行pop，只要简单地减少这个下标值即可。
a. 使用静态数组实现堆栈操作，代码如下：
a#include "stack.h"
#include <assert.h>
#define STACK_SIZE 100 // 设置堆栈大小
// 存储堆栈中值的数组和一个指向堆栈顶部元素的指针
static STACK_SIZE stack[STACK_SIZE];
static int top_element = -1;
// push
void push(STACK_TYPE value)
{
assert(!is_full()); // 设置断言，检查堆栈是否已满
top_element += 1； // 压栈
stack[top_element] = value;
}
// pop
void pop(void)
{
assert(!is_empty()); // 设置断言，检查堆栈是否为空
top_element -= 1; // 退栈
}
// top
STACK_TYPE top (void)
{
assert (!is_empty()); // 设置断言，检查堆栈是否为空
return stack[top_element]; // 返回栈顶的元素值
}
// is_empty
int is_empty(void)
{
return top_element == -1;
}
// is_full
int is_full(void)
{
return top_element == STACK_SIZE - 1 ;
}
b. 使用动态数组实现堆栈操作，代码如下：
b#include "stack.h"
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#include <assert.h>
// 用于存储堆栈元素的数组和指向堆栈顶部元素的指针
static STACK_TYPE *stack;
static size_t stack_size;
static int top_element = -1;
// create_stack
void creat_stack(size_t size) // 向用户传递一个参数用来指定堆栈大小
{
assert(stack_size == 0);
stack_size = size;
stack = malloc(stack_size * sizeof(STACK_TYPE));
assert(stack != NULL);
}
// destroy_stack
void destroy_stack(void) // 销毁堆栈，也就是内存释放
{
assert(stack_size > 0);
stack_size = 0; // 将堆栈大小重新设置为0
free(stack);
stack = NULL; // 将指针重新设置为0
}
// push
void push(STACK_TYPE value)
{
assert(!is_full());
top_element += 1;
stack[top_element] = value;
}
// pop
void pop(void)
{
assert(!is_empty());
top_element -= 1;
}
// top
STACK_TYPE top(void)
{
assert(!is_empty());
return stack[top_element];
}
// is_empty
int is_empty(void)
{
assert(stack_size > 0); // 设置断言，防止任何堆栈函数在堆栈未创建前就被调用
return top_element == -1;
}
// is_full
int is_full(void)
{
assert(stack_size > 0); // 设置断言，防止任何堆栈函数在堆栈未创建前就被调用
return top_element == stack_size - 1;
}
c. 使用动态链式实现堆栈操作，代码如下：
c#include "stack.h"
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#include <assert.h>
#define FALSE 0
// 定义一个结构用于存储堆栈元素，其中link字段指向堆栈的下一个元素
typedef struct STACK_NODE{
STACK_TYPE value;
struct STACK_NODE *next;
} StackNode;
// 指向堆栈中第一个节点的指针
static StackNode *stack;
// creat_stack
void creat_stack(size_t size)
{
// 是个空函数，因为链式堆栈不会填满，所以is_full始终返回假
}
// destroy_stack
void destroy_stack(void)
{
while(!is_empty()) // 从堆栈中弹出元素，直到堆栈为空
pop();
}
// push
void push(STACK_TYPE value)
{
StackNode *new_node;
new_node = malloc(sizeof(StackNode));
assert(new_node != NULL);
new_node->value = value;
new_node->next = stack;
stack = new_node;
}
// pop
void pop(void)
{
StackNode *first_node;
assert(!is_empty());
first_node = stack;
stack = first_node->next;
free(first_node);
}
// top
STACK_TYPE top(void)
{
assert(!is_empty());
return stack->value;
}
// is_empty
int is_empty(void)
{
return stack == NULL;
}
// is_full
int is_full(void)
{
return FALSE;
}
3. 队列
队列的数据结构特点是先进先出(First-IN First-OUT, FIFO)。
1.) 队列接口
队列的修改是依先进先出的原则进行的，新加的元素总是加入队尾，销毁的元素总是队列头上的。这也正好准确地描述了现实生活中排除的实际体验。一个队列接口可以如下：
d#include <stdlib.h>
#define QUEUE_TYPE int
// create_queue 创建一个队列，参数指定队列可以存储元素的最大数量。
void create_queue (size_t size);
// destroy_queue 销毁一个队列
void destroy_queue (void);
// insert 向队列添加一下新元素，参数就是需要添加的元素
void insert (QUEUE_TYPE value);
// delete 从队列中移除一个元素，并将其丢弃
void delete(void);
// first 返回队列第一个元素的值，但不修改队列本身
QUEUE_TYPE first (void);
// is_empty 如果队列为空，返回TRUE，否则返回FALSE
int is_empty (void);
// is_full 如果队列已满，返回TURE，否则返回FALSE
int is_full (void);
2.) 实现队列
实现队列的方法可以是动态数组、链表和循环队列(circular array)，现在主要介绍循环队列的实现。它需要两个指针，一个指向队列中第一个元素(front)，一个指向队列最后一元素(rear)。示例图如下：
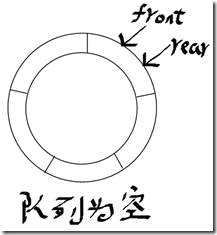
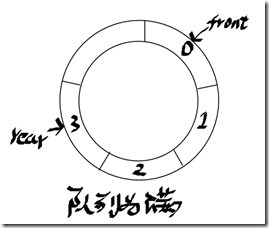
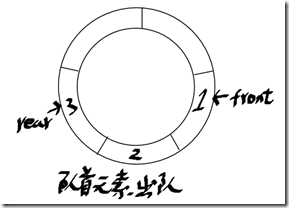
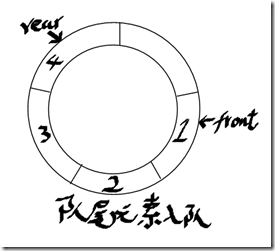
注：上面队列为满的队列，实际上没有满，目的是为了让front和rear不指向同一位置，因为队列为空时，它们是指向同一个位置的。这样便可以区分队列为空或为满了。
当队列为空时，front 与 rear关系为：(rear + 1) % QUEUE_SIZE == front
当队列为满时，front 与 rear关系为：(rear + 2) % QUEUE_SIZE == front
代码如下：
d// 用一个静态数级实现的队列
#include "queue.h"
#include <stdlib.h>
#include <assert.h>
#define QUEUE_SIZE 100 // 队列中元素的最大数量
#define ARRAY_SIZE (QUEUE_SIZE + 1) // 数组的长度
// 用于存储队列元素的数组和指向队列头，尾的指针
static QUEUE_TYPE queue[ARRAY_SIZE];
static size_t front = 1;
static size_t rear = 0;
// insert
void insert(QUEUE_TYPE value)
{
assert(!is_full());
rear = (rear + 1) % ARRAY_SIZE;
queue[rear] = value;
}
// delete
void delete(void)
{
assert(!is_empty());
front = (front + 1) % ARRAY_SIZE;
}
// first
QUEUE_TYPE first(void)
{
assert(!is_empty());
return queue[front];
}
// is_empty
int is_empty(void)
{
return (rear + 1) % ARRAY_SIZE == front;
}
// is_full
int is_full(void)
{
return (rear + 2) % ARRAY_SIZE == front;
}
以上参考：http://student.zjzk.cn/course_ware/data_structure/web/zhanhuoduilie/zhanhuoduilie3.2.2.1.htm
4. 二叉树
树是一种重要的非线性数据结构，树形结构是结点之间有分支，并具有层次关系的结构。二叉树(binary search tree)是树中一种特殊形式，它的每个节点最多有两个子树，分别为左子树和右子树。最上面的那个节点，称为树根，它没有父节点。没有子节点的节点称为叶节点(leaf node)。
二叉树有个额外的属性：每个节点的值比它的左子树的所有节点的值都要大，但比它的右子树的所有节点的值都要小。
1.) 二叉树接口
#define TREE_TYPE int // 树值的类型
// insert 向树添加一个新值，参数是需要被添加的值，它必须是原先不存在于树中
void insert(TREE_TYPE value);
// find 查找一个特定的值，这个值作为第1参数传递给函数
TREE_TYPE *find(TREE_TYPE value);
// pro_order_traverse 执行树的前序遍历，它的参数是一个回调函数指针，它所指向的函数将在树中处理每个节点被调用，节点的值作为参数传递给这个参数
void pre_order_traverse (void (*callback) (TREEE_TYPE value));
2.) 实现二叉树
d#include "tree.h"
#include <assert.h>
#include <stdio.h>
#define TREE_SIZE 100
#define ARRAY_SIZE (TREE_SIZE + 1)
static TREE_TYPE tree[ARRAY_SIZE];
// left_child 计算一个节点左子树的下标
static int left_child (int current)
{
return current * 2;
}
// right_child 计算一个节点右子树的下标
static int right_child (int current)
{
return current * 2 + 1;
}
// insert
void insert (TREE_TYPE value)
{
int current;
// 确保值为非零，因为零用于提示一个未使用的节点
assert(value != 0);
// 从根节点开始
current = 1;
// 从合适的子树开始，直到到达一个叶节点
while(tree[current] != 0)
{
if (value < tree[current])
current = left_child(current);
else
{
assert(value != tree[current]);
current = right_child(current);
}
assert(current < ARRAY_SIZE);
}
tree[current] = value;
}
// find
TREE_TYPE *find(TREE_TYPE value)
{
int current;
// 从根节点开始，直到找到那个值，进入合适的子树
currtne = 1;
while (current < ARRAY_SIZE && tree[current] != value)
{
if (value < tree[current])
current = left_child(current);
else
current = right_child(current);
}
if (current < ARRAY_SIZE)
return tree + current;
else
return 0;
}
// do_pre_order_traverse 执行一层前序遍历，这个函数用于保存当前正在处理的节点信息，并不是用户接口的一部分
static void do_pre_order_traverse(int current, void (*callback) (TREE_TYPE vaule))
{
if (current < ARRAY_SIZE && tree[current] != 0)
{
callback(tree[current]);
do_pre_order_traverse(left_child(current));
do_pre_order_traverse(right_child(current));
}
}
// pre_order_traverse
void pre_order_traverse(void (*callback) (TREE_TYPE value))
{
do_pre_order_traverse(1, callback);
}
