数论笔祭 - 林学长的第二数学

林学长讲课笔记

极限

\(\lim_{x \to x_0} f(x)\)

考虑运算法则：

• 一般来说，函数的和差商积的极限等于函数的极限的和差商积。

但是例外：

\[\lim_{x \to 3} \frac {x - 3}{x^2 - 9} \]

考虑极限约去 \(x - 3\) 得到：

\[\lim_{x \to 3} \frac 1 {x + 3} = \frac 16 \]

如果约不掉？但是……

\[\lim_{x \to 1} \frac {2x - 3} {x^2 - 1} \]

考虑 \(2x - 3\) 不为 \(0\)，所以 \(= \infty\)

总结到一般的高次多项式？

\[\lim_{x \to \infty} \frac {a_0 x^m + \cdots}{b_0 x^n + \cdots} \]

• 若 \(m > n\) 则 \(= \infty\)

• 若 \(m = n\) 则 \(= \frac {a_0}{b_0}\)

• 若 \(m < n\) 则 \(= 0\)

发散？收敛？看是否存在可数的上下界

\[\lim_{x \to \infty} \frac {\sin x} x \]

考虑 \(\lim \frac 1x = 0\)，而 \(\sin x\) 是有界函数，故 \(\lim \frac {\sin x} x = 0\)（\(0\) 乘上一个有界函数）

---

重要的极限：

\[\lim_{x \to 0} \frac {\sin x} x = 1 \tag{1} \]

\[\lim_{x \to \infty}(1 + \frac 1 x)^x = e \tag{2} \]

可以利用夹逼定理证明 \((1)\)。考虑：

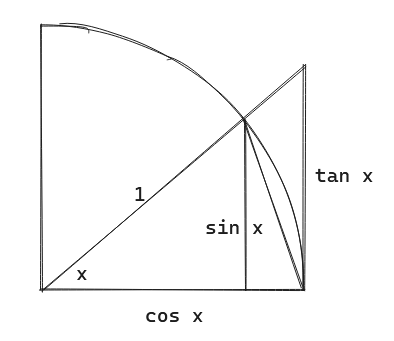
发现三个面积有：

\[\frac 12 \sin x \le \frac 12 x \le \frac 12 \tan x \]

整理一下：

\[1 \le \frac x {\sin x} \le \frac 1 {\cos x} \]

根据夹逼定理，有 \(\lim \frac x {\sin x} = 1\)。

---

导数

对于 \(f(x)\)，\(f'(x)\) 表示函数在 \(x\) 时的斜率。

\[f'(x) = \lim_{\Delta x \to 0} \frac {f(x + \Delta x) - f(x)}{\Delta x} = \frac {dy} {dx} \]

常见的导数：

\(f(x)\)	\(f'(x)\)
\(C\)	\(0\)
\(x^\mu\)	\(\mu x ^{\mu - 1}\)
\(\sin x\)	\(\cos x\)
\(\cos x\)	\(-\sin x\)
\(a^x\)	\(a^x \ln a\)
\(\log_ax\)	\(\frac 1{x \ln a}\)

运算法则：

• \([u(x) \pm v(x)]' = u'(x) \pm v'(x)\)

• \([u(x)v(x)]' = u(x)v'(x) + u'(x)v(x)\)

• \([\frac {u(x)}{v(x)}]' = \frac {u'(x)v(x) - u(x)v'(x)}{v^2(x)}\) 这是子导母不导减去母导子不导。

考虑一下常用导数：

\[f(x) = \tan x = \frac {\sin x}{\cos x} = \frac {\cos^2 x + \sin^2 x}{\cos^2 x} = \frac 1 {\cos^2 x} \]

对于反函数：

\[f(x) = y \iff f^{-1}(y) = x \]

有：

\[[f^{-1}(x)]' = \frac 1 {f'(f(x))} \]

于是对于 \(f(x) = \arctan x\)，有：

\[\begin{aligned} (\arctan x)' &= \frac 1 {\tan'(\arctan x)} \\ &= \cos^2 (\arctan x) \\ &= \frac 1 {1 + \tan^2 (\arctan x)} \\ &= \frac 1 {1 + x^2} \end{aligned} \]

对于复合函数 \(y = f(g(x))\) 求导。

令 \(u = g(x)\)，于是 \(\to y = \frac {du}{dy}, u' = g'(x) = \frac {dx}{du}\)。

也就是 \(y' = f'(x) \cdot g'(x)\)。

例如 \(e^{x^3}\) 的导数相当于 \(f(x) = e^x, g(x) = x^3\) 函数复合求导。

于是 \((e^{x^3})' = f'(x)\cdot g'(x) = e^x \cdot 3x^2\)。

---

柯西中值定理 描述的是：

若在 \([a, b]\) 上 \(f(x), F(x)\) 连续，在 \((a, b)\) 上 \(f(x), F(x)\) 可导且 \(\forall x \in (a, b) F'(x) \ne 0\) 那么一定至少存在一个点 \(\xi\) 使得：

\[\frac {f(a) - f(b)}{F(a) - F(b)} = \frac {f(\xi)}{F(\xi)} \]

那么对于洛必达法则：

• 当 \(x \to a\) 时，\(f(x), F(x)\) 都趋近于 \(0\)。

• \(\lim_{x \to a} \frac {f'(x)}{F'(x)}\) 存在（或为无穷大）

那么：

\[\lim_{x \to a}\frac {f(x)}{F(x)} = \lim_{x \to a} \frac {f'(x)}{F'(x)} \]

考虑转化为：

\[\lim_{x \to a}\frac {f(x) - 0}{F(x) - 0} \]

如果满足了第一个条件，那么可以依据柯西中值定理构造出：

\[\frac {f(x) - f(a)}{F(x) - F(a)} = \frac {f'(\xi)}{F'(\xi)} \]

\(\xi\) 在 \(a, x\) 之间。那么原式成立。

既然洛必达法则存在，那么考虑泰勒展开逼近：

\[f(x) = \sum_{n = 0}^\infty \frac {f^{(n)}}{n!} x^n \]

考虑展开 \(\ln(1 + x)\) 有：

\[f^{(n)}(0) = (-1)^{n - 1}(n - 1)! \]

于是

\[\begin{aligned} \ln(1 + x) &= x - \frac {x^2} 2 + \frac {x^3} 3 - \frac {x ^ 4} 4 + \cdots \\ &= \sum_{n = 1}^{\infty} \frac {(-1)^{n - 1}}n x^n \end{aligned} \]

---

勾股数组定理

对于每一个本原勾股数组 \((a, b, c)\)，都可以从如下公式推出：

本原勾股数组：满足 \(\gcd(a, b, c) = 1\) 且 \(a^2 +b^2 = c^2\) 的数组。

\[a = st, b = \frac {s^2 - t^2} 2, c = \frac {s^2 + t^2} 2 \]

特别的，如果取 \(t = 1\)，那么可以得到三元组：

\[(s, \frac {s^2 - 1}2, \frac {s^2 + 1} 2) \]

欧拉函数

对于 \(\varphi(x)\)：

• 基于概率的证明

• 基于积性函数的证明

\[a^{\varphi(p)} \equiv 1 \pmod p \]

考虑 \(\Z_p\) 的完全剩余系的大小，即是 \(\varphi(p)\)。

Fib 数列周期性

对于 \(f: \Z_n\)，记其循环长度为 \(N(n)\)。

可以有：

\[\gcd(x, y) = 1 \implies N(x y) = \mathit{lcm}(N(x)N(y)) \]

也可以有：

\[N(p^k) = p^{k - 1}N(p) \]

那么现在的问题是 \(N(p)\)，观察可知：

\[N(p) = \begin{cases} p - 1, p \equiv 1 \pmod {10} \\ \end{cases} \]

• \(p \equiv \pm 1 \pmod {10} \implies N(p) | p - 1\)

• \(p \not\equiv \pm 1 \pmod {10} ~and~ p \not\equiv 5 \pmod {10} \implies N(p) | 2p + 2\)

• \(\cdots\)

但是考虑有点小小的刻意，所以考虑 \(\bmod 5\)。

\[N(p) | \begin{cases} p - 1, p \equiv \pm 1 \pmod 5 \\ 2p + 2, p \equiv \pm 2 \pmod 5 \\ \end{cases} \]

特殊的 \(N(5) = 20\)。

特殊的等式：

• \(f_{n-1}^2 + f^{2}_{n+1} = f_{2n}\)

---

佩尔方程

\[x^2 - Dy^2 = 1 \]

可以如下解：

\[\begin{aligned} (x + \sqrt D y) (x - \sqrt D y) = 1 \\ (x^2 + Dy^2 + 2\sqrt D x y)(x^2 + Dy^2 - 2\sqrt D x y) = 1 \\ (x^2 + Dy^2) - 4D x^2y^2 = 1 \\ (x^2 + Dy^2) - D (2xy)^2 = 1 \end{aligned} \]

于是如果可以解出一组 \((x, y)\)，那么可以构造 \((x^2 + Dy^2, 2xy)\) 作为新的解。

丢番图逼近

\[x^2 - Dy^2 = k \]

连分数

\[\frac {p_n}{q_n} = a_0 + \cfrac {1} {a_1+ \cfrac {1} {a_2 + \cfrac {1} {\ddots + \cfrac 1 {a_n}}}} \]

可以简单记为一个序列 \([a_0, a_1, a_2, \cdots ]\)。

连分数递推公式，用于求解 \(p_n, q_n\)。

\[p_0 = a_0, p_1 = a_0 a_1 + 1 \\ q_0 = 1, q_1 = a_1 \]

有：

\[\begin{aligned} p_n = a_n p_{n - 1} + p_{n - 2} \\ q_n = a_n q_{n - 1} + q_{n - 2} \end{aligned} \]

考虑归纳证明即可。