算法学习笔记(∞)：杂项

1.算法学习笔记(∞)：杂项2023-08-17

杂项

杂项

$\mathcal {I~Hate~NTT~}$

\sum_{k} {(\binom{n}{k})}^{2} (\binom{3 n + k}{2 n}) = {(\binom{3 n}{n})}^{2}

$\sum_k \binom nk ^2 \binom {3n + k}{2n} = \binom{3n}n ^2$

代码规范

边界开闭找清楚
指针空悬判清楚
时空复杂算清楚
特殊情况模清楚
math.h 加清楚
思路正确证清楚

卡常小技巧

using uint = unsigned int，在代码中非负的地方都用 uint，需要注意溢出的可能，尤其是两者相减的时候。
利用 fread 优化读入，主要是代码有点长，一般用 cin 是完全够的。
取模的时候有 x >= mod && (x -= mod); 优化掉 if。
注意 bitset 的 count 是 $O(\frac n w w)$ 也就是 $O(n)$ 的。
注意数组的顺序，导致 cache 的问题。运算不一定比随机空间访问慢。
离散化用你妈的 map 就是在作死！

算法优化的本质

优化算法其实就是对于信息的充分利用，将信息的价值最大化。

无论是性质还是什么的，都属于信息的部分。

做题思路小结

要有属于自己的一套

确定题目问题范围，暴力题，DP题，性质题，结论题，打表题，数学题还是什么的，限制一个大范围。
尝试简化问题，对于问题进行分治，化简为一个一个小问题，逐步的解决。
尝试规约问题，将一个问题规约为已知的知识，合理外推，从而找到合适的做法。
尝试一般化问题，如果能够找到一般化的解，那么一定可以特殊化到这道题来。
尝试抽象问题，将问题用数学描述（这很抽象了……），利用数学的角度解决问题。

另外的就是一些抽象的灵感了，不过寻找灵感也是需要过程的。

尝试可视化，有图有真相。
模拟最朴实的算答案的过程，理清楚细节即原理。
顺难则逆。
多方向化简题意，转化题意，理清限制。
充分利用 随机数据 来骗分（ODT!）
充分利用变化总量很少的信息（比如类似于 $\sum \frac ni = O(n \log n)$ 的信息）
从题目的描述中找到算法的流向，以及优化的方向。

乱搞的一些小思路：

对于求期望，那就直接随机模拟算期望。但是一般得不出来准确值……
随机打乱排列，从而保证某随机算法的期望复杂度。
充分条件多验证几次就充要了？

根号优化

根号优化常常与存在某个序列满足 $\sum a_i \le 10^5$ 相关，例如字符串中的 $\sum |T_i| \le 10^5$ ，例如数列中 $\sum cnt_x = n$ ， $cnt_x$ 即 $x$ 出现的次数。

这种时候，常使用 $\ge \sqrt n$ 的部分 $O(n)$ 暴力，而 $\le \sqrt n$ 的部分统一 $O(n \sqrt n)$ 做。

或者说，存在两种暴力，一种是 $O(\frac {n^2} l)$ ，一种是 $O(nl)$ ，那么就可考虑根号分治。

根号分治与一般分治不同，一般分治面向的是问题规模，而根号分治则面向的是信息规模。

记忆化搜索

这是最核心的方法，是开始，也是终止。

记忆化搜索是最简单的，但是也是最直观的符合优化算法的本质的方法。

核心在于利用变量中的不变量，以此求出不同状态下的答案。

重点就转化为状态的定义，状态不应该和方案相关，它可以是一个性质，一个区间，一个点，甚至一个边。而状态也不应该被后面的状态限制。

基于边的记忆化

这是个小技巧，已经用这个方法切了两道 $T1$ 了 QwQ。

其用的前提在于对于一条边，经过前无论状态如何都不会影响后面的答案。

其复杂度为 $O(m)$ ，但是需要带上 $6$ 倍的常数，不过可以接受。

后来复杂度可能伪了，应该是 $O(\sum deg_x^2)$ 的，但是当时我测菊花图并没有这个问题，似乎当时测的是无向图。

UPDATE：现在可能有一个复杂度正确的做法，三度化，使得每一个点的度数不超过 $3$ ，这样复杂度就是正确的了，只是会带一个 $2 \times 3 \times 3$ 的常数，不优秀。

动态规划

属于是特类的记忆化了。通过增量维护某个信息，然后基于前面某个状态的信息求解。

DDP 就属于动态的动态规划，本质在于利用矩阵（广义）维护增量的叠加，然后统一转移。

动态规划思考的方向

首先应该想一个比较朴素的暴力，如果难以下手，可以通过（找性质）增加枚举量来获得一个高复杂度的算法。
尝试优化算法本身，剪掉重复枚举的情况。
如果算法本身足够优秀，尝试寻找性质，减少枚举量。
难以发现有用的性质，尝试更换状态，设计一个更加简单的状态。

动态规划优化小技巧

单调性，这是十分重要的一个性质。
差分的使用，可能差分也具有单调性，如 [USACO21JAN] Minimum Cost Paths。类似如 $f_{i, j} = \max(f_{i - 1, j}, f_{i, j - 1} + cost)$ 的这种转移都可以考虑单调性。甚至决策点的单调，例如 CF573E。两者本质差不多。然后利用线段树统一转移即可。
线段树优化转移，统一转移。
RMQ 优化，如果可以滑动窗口自然是最好，如果不可以，可以考虑 ST 表后加元素，复杂度 $O(\log n)$ 不均摊。
四边形不等式，决策单调性，斜率优化……可能就需要用到 CDQ 分治了。
利用数学相关知识，矩阵，生成函数，插值等等。
外面可以再讨一个 WQS 二分

关于树上问题的一点总结

树上每一个点求答案

目前有三种套路：

换根 DP
基于边的记忆化
找到一个点对于其他点的贡献

如何理解依据边的记忆化搜索：可以理解为对于一个点，不同的根会造成不同的父亲，于是记忆化每一个点给不同父亲的贡献即可，利用三度化可以很好的避免复杂度的问题。

关于树上左右肺，食道与胃的部分内容

对于找到一个点 x 对其他点做出的贡献，一种简单的想法是 dfs，然后维护四部分信息，我称之为左肺，右肺，支气管（食管）和胃。其中各部分存有如下信息：

左肺：存 x 子树外已经遍历过的点的信息。
右肺：存 x 子树外还没有便利过的信息。
支气管：存 x 祖先的信息
胃：存 x 子树的信息。

对于各部分的维护大概分为如下几个步骤：

进入 x 时，保存左肺的信息，并把 x 在右肺删除。
递归进入子树，加入 x 作为子树的信息。
合并子树信息，得到胃的信息，准备求答案。值得注意的是，如果信息满足差分，那么左肺中的新增的信息其实就是胃的信息，否则，可以通过启发式合并以及可持久化的方式获取子树信息以及左肺的信息。
求答案。
回溯，将 x 加入左肺中。

可以通过这个方法做的题：

关于树上基于 `dfn` 序的种种操作

子树求和，转化为连续 dfn 区间求和。
链上求和，可以利用树剖转化为 $O(\log n)$ 个连续的 dfn 区间进行求和，这是 $O(\log^2 n)$ 的。如果不需要链修改，只是单点修边权，可以将边权下放到点权，利用 dfn 子树加，单点查即可，这是 $O(\log n)$ 的。
判断祖先关系，利用 dfn 以及 edfn 即可判断。
找到祖先关系下所在的那颗子树的大小，利用上一种方法，在 G[x] 上二分即可。这比倍增复杂度小多了。
与深度相关的子树信息问题，利用 dep 为版本从小到大建立主席树，用 dfn 为下标作为查询的部分。可以理解为按照 dep 差分，但是左边的差分树种没有 dfn 内的信息，所以可以直接忽略。如图，蓝色是主席树差分的部分，绿色是 dfn 限制的部分，橙色是想要的部分：可以在 dep 以上部分并没有任何信息交。
如何判断两棵树的某两个子树是否有交，# [IOI2018] werewolf 狼人，在两棵树上，同一个点对应了两个 dfn，于是可以把它看作平面上的一个点，而子树的 dfn 是连续的，所以问题转化为求一个矩形是否存在一个点，这利用主席树或者离线扫描线是好做的。
dfn 是入栈的顺序，类似的，其实有出栈序，也就是每个结点离开 dfs 的顺序。一个较好的结论是在 dfs 过程中，x 到其某个父亲 p 的出栈序区间内被影响到的只有其间的那些链。类比左肺右肺，出栈序比 x 小的是左肺和胃，出栈序比 p 大的是 p 的祖先以及右肺的部分。注意到此时右肺并没有被访问到，也就是没有信息。所以排除上述位置，区间内只有 x 到 p 这条链的信息了。

关于树上倍增优化建图的问题

有没有一种可能，倍增建图并不需要划分为 $O(\log n)$ 个区间，而是类似于 Spare Table 的做法，两个区间即可。（当然，前提是如此不影响正确性。

【XR-1】逛森林 - 洛谷

关于树上背包

树上背包变化非常的多，很多情况下考试的时候我都做不出来。

加换根的复杂度

如果只是树上正常的背包，复杂度是 $O(n^2)$ 无疑，但是如果加上换根，那么在换根的时候复杂度无法保证，容易变成 $O(n^3)$ 。

如果存在 $f, g$ 同阶贡献的性质，那么可以将 $g$ 限制在 $siz_x$ 内，也就是与 $f$ 同阶，同样，前后缀卷积也可以限制在 $\max siz_y$ 内，使的其复杂度可以沿用背包的复杂度分析，成为 $O(n^2)$ 。

关于树上分治

点分治不需要额外的对于边进行处理，在一般情况下比边分治优秀。
边分治由于只会产生两个分支，所以只需要简单构建一次数据结构，不需要复杂的讨论，在某些情况下非常有优势。
边分治在处理点权的时候需要将点权在三度化时下放到边权上，前提是信息满足幂等。

补充：关于 dfs 的一点性质

在无向图上 dfs 树不存在横边，要么是树边，要么是返祖边，在一些树上构造题中很有用。

计数题/数学题

一般来说，还是有套路的：

组合计数，利用组合数直接求解。
转换计数，也就是转换模型，再利用组合计数。而转换也有一定的套路：
- 转化为操作之间的关系然后计数。有 $2023.08.23$ flip， $..08.26$ explorer， $..08.28$ ring
加法原理，分情况讨论。
容斥原理，总方案数好算，但是目标方案数不好算，就可以考虑这么算。有 $2023.08.28$ ring，mex（题解做法）， $..08.30$ au
- 反射容斥，或者叫折线容斥，用于处理类似卡特兰数的计数，但是限制是上下界，见格路径博文。
乘法原理，将答案分成两个部分，并且每个答案两个部分间有共用的部分。有 $2023.08.28$ mex

别魔怔，打表找规律！

一些小技巧

遇到形如 $\le \lfloor \frac n2 \rfloor$ 的限制，那么考虑容斥，因为至多只有一个不满足。
遇到形如 $f_{i, j, k}$ 表示某个选了 $j$ 个，总共选了 $k$ 的情况，如果并不关注具体的 $j, k$ ，那么将这一维改为 $j - k$ 进行转移是合理的。
有些时候可以构造双射将部分情况直接给干掉。

关于一些常见式子化简思路

不要魔怔，尝试是否能够递推！！！！！！！

方差： $\sum (a_i - \bar a)^2 = \sum a_i^2 + n \bar a^2 - 2\bar a \sum a_i = \sum a_i^2 - \frac 1n (\sum a_i)^2$ 。如果和是定值，那么我们只需要最小化每一段即可，类比 $\mathrm{Var}(X) = E(X^2) - E(X)^2$ 。
$E[(\sum a_j)^k]$ ，利用二项式形式： $E[(\sum a_j)^k] = \sum \binom ki E[a_n^i] E[C^{k - i}]$ ，注意前提是 $a_i$ 之间相互独立！
遇到计算复杂度为 $O(\sqrt[k] n)$ 的东西将 $k = 1, 2$ 的时候拆出来单独处理。
与 $\gcd$ 相关的考虑 $[x = 1] = \sum_{d | x} \mu (d)$ 以及 $x = \sum_{d | x} \varphi(d)$ ，也就是莫比乌斯反演。
如果式子感觉没法化简了（没有通项）可以考虑递推，利用矩阵快速幂优化至 $O(\log n)$ 。注意相关量是否也需要并行递推，并注意增广矩阵的使用。
遇到与幂次相关的玩意考虑斯特林： $n^k = \sum_k {k \brace i} n^{\underline i}$ 。

就算摆烂也要考虑插值！

斯特林数

谁说第一类斯特林数没有什么用？

考虑 [FJOI2016] 建筑师，很巧妙的利用了第一类斯特林数的意义，转化了问题。

其主要的特征是出现了分组，并且组内存在 $(n - 1)!$ 中方案，那么可以转化为圆排列，从而转化为第一类斯特林数。

斯特林数的常见用法：

普通幂转下降/上升幂： $n^k = \sum_k {k \brace i} n^{\underline i} = \sum_k {k \brace i} (-1)^{k - i} n^{\bar i}$ 。
上升/下降幂转普通幂： $n^{\underline k} = \sum_i {k \brack i} (-1)^{k - i} x^i, x^{\bar k} = \sum_i {k \brack i} x^i$ 。

如果不嫌麻烦，那么存在： $\sum_k {n \brack k} {k \brace m}(-1)^{n - k} = \sum_k {n \brace k} {k \brack m}(-1)^{n - k} = [n = m]$ 。但是为什么不用莫比乌斯反演？

组合数前缀和

设

S (n, m) = \sum_{i = 0}^{m} (\binom{n}{i})

$S(n, m) = \sum_{i = 0}^{m} {n \choose i}$

考虑莫队转移：

S (n, m) = S (n, m - 1) + (\binom{n}{m}) S (n, m) = 2 \times S (n - 1, m) - (\binom{n - 1}{m})

$S(n, m) = S(n, m - 1) + {n \choose m} \\ S(n, m) = 2 \times S(n - 1, m) - {n - 1 \choose m}$

而还有一种 $O(n \sqrt n)$ 预处理， $O(\sqrt n)$ 询问的方法（其实还可以减少其常数以提升其上界），如图：

每隔 $\sqrt n$ 设置一个断点，在杨辉三角上向上跳即可。

预处理空间是 $O(n \sqrt n)$ 的，但是可以通过离线变为 $O(\sqrt n)$ ，如果在每一层微调，那么可以做到 $\sum_{i = 1}^n \sqrt i$ ，虽然还是 $O(n \sqrt n)$ ，但是小常数。

单位根反演

[n | a] = \frac{1}{n} \sum_{k = 0}^{n - 1} ω_{n}^{a k}

$[n|a] = \frac 1n \sum_{k = 0}^{n - 1} \omega_n^{ak}$

考虑求 $[x \equiv y \pmod p]$ ，有 $p | x - y$ 。

于是

= \frac{1}{p} \sum_{k = 0}^{p - 1} ω_{p}^{(x - y) k} = \frac{1}{p} \sum_{k = 0}^{p - 1} ω_{p}^{x k} ω_{p}^{- y k}

$= \frac 1p \sum_{k = 0}^{p - 1} \omega_p^{(x - y)k} \\ = \frac 1p \sum_{k = 0}^{p - 1} \omega_p^{xk} \omega_p^{-yk} \\$

P5591，利用有封闭形式的式子和单位根反演可以批量生产好题，可见我的 PPT share-math。

生成函数与多项式

多项式的多项式前缀和

对于 $n$ 阶多项式 $f$ 已知 $f(0), f(1), \cdots, f(n)$ 。需要求：

S (x) = \sum_{i = 0}^{k} f (i) x^{i}

$S(x) = \sum_{i = 0}^{k} f(i) x^i$

存在结论，存在一个 $n$ 阶多项式 $g$ 满足：

S (k - 1) = x^{k} g (k) - g (0)

$S(k - 1) = x^k g(k) - g(0)$

可以参见 whx 的 blog。

所以可以考虑 $O(n)$ 插值求出 $g(k + 1)$ 即可求出 $S(k)$ 。

生成函数的前缀和

注意到：

S_{x} = \sum F_{x - i} \times 1

$S_x = \sum F_{x - i} \times 1$

那么实际上是：

S (x) = F (x) \frac{1}{1 - x}

$S(x) = F(x) \frac 1 {1 - x}$

在某些生成函数题可能有奇效。

$O(n)$ 求连续点值多项式单点取值

对于 $n + 1$ 个点 $(x_i, y_i)$ ，考虑拉格朗日差值公式：

f_{i} (x) = \prod_{j \neq i} \frac{x - x_{j}}{x_{i} - x_{j}}

$f_i(x) = \prod_{j \ne i} \cfrac {x - x_j}{x_i - x_j}$

最终的式子是：

f (x) = \sum y_{i} f_{i} (x)

$f(x) = \sum y_i f_i(x)$

考虑如何快速求出 $f_i(x)$ 。

首先是分子部分，可以考虑利用前后缀和。

其次是分母，假定 $x_0$ 最小， $x_n$ 最大，所以对于 $x_i$ 的分母部分为：

(x_{i} - x_{0})! * (- 1)^{n - i} (x_{n} - x_{i})!

$(x_i - x_0)! * (-1)^{n - i} (x_n - x_i)!$

$O(n)$ 预处理阶乘即可 $O(1)$ 算出。

于是剩下的问题就是如何对于所有的分母求逆。

类比阶乘求逆元的方法，先求出前缀积，求逆后逆推出前缀积的逆。利用这两者即可求出每一项的逆。复杂度为 $O(n + n + \log n) = O(n)$ 。

于是 $O(n)$ 算出最终答案即可，总复杂度为 $O(n)$ 。常数还行，大概为 $8$ ，因人而异。

// 来自 https://www.luogu.com.cn/problem/AT_arc033_4
// x_0 = 0, x_n = n
// 循环较多是考虑到缓存友好问题

lint qpow(lint a, int x) {
    lint r = 1;
    for (; x; x >>= 1, a = a * a % mod)
        if (x & 1) r = r * a % mod;
    return r;
}

int n, x;
lint y[N];
lint pre[N], suf[N];
lint fac[N], rfac[N];
lint up[N], down[N];
lint tmp[N], dinv[N];

int main() {
    scanf("%d", &n); ++n;
    for (int i = 1; i <= n; ++i)
        scanf("%lld", y + i);
    scanf("%d", &x);

    pre[0] = suf[n + 1] = 1;
    for (int i = 1; i <= n; ++i)
        pre[i] = pre[i - 1] * (x - i + 1) % mod;
    for (int i = n; i; --i) 
        suf[i] = suf[i + 1] * (x - i + 1) % mod;

    fac[0] = rfac[0] = 1;
    for (int i = 1; i <= n; ++i)
        fac[i] = fac[i - 1] * i % mod;
    for (int i = 1; i <= n; ++i)
        rfac[i] = rfac[i - 1] * (mod - i) % mod;

    for (int i = 1; i <= n; ++i)
        up[i] = pre[i - 1] * suf[i + 1] % mod;

    for (int i = tmp[0] = 1; i <= n; ++i) {
        down[i] = fac[i - 1] * rfac[n - i] % mod;
        tmp[i] = tmp[i - 1] * down[i] % mod;
    } tmp[n] = qpow(tmp[n], mod - 2);

    for (int i = n; i; --i) {
        dinv[i] = tmp[i] * tmp[i - 1] % mod;
        tmp[i - 1] = tmp[i] * down[i] % mod;
    }

    lint ans = 0;
    for (int i = 1; i <= n; ++i) {
        ans = (ans + y[i] * up[i] % mod * dinv[i] % mod) % mod;
    } printf("%lld\n", ans);
    return 0;
}

牛顿级数求点值

牛顿级数形如：

f (x) = \sum_{i \geq 0} c_{i} (\binom{x}{i})

$f(x) = \sum_{i \ge 0} c_i {x \choose i}$

考虑差分在 $0$ 处的取值：

(Δ^{n} f) (0) = \sum_{i \geq 0} c_{i} (\binom{0}{i - n})

$(\Delta^n f)(0) = \sum_{i \ge 0} c_i {0 \choose i - n}$

由于仅 ${0 \choose 0} = 1$ 所以 $= c_n$ 。

问题转化为求 $\Delta^k f(0)$ ，根据差分序列性质：

Δ^{k} f (0) = \sum_{i} (- 1)^{n - i} (\binom{n}{i}) f (i)

$\Delta^k f(0) = \sum_{i}(-1)^{n - i} {n \choose i} f(i)$

这是一个卷积形式，所以可以 $O(n \log n)$ 求出所有的 $c_i$ 。

处理出 $c_i$ 我们就可以 $O(n)$ 的求出 $f(x)$ 了，同时，可以利用下降幂转普通多项式的做法 $O(n \log^2n)$ 的搞出普通多项式，这比拉格朗日大常数求逆 $O(n \log^2 n)$ 快（但是限制大）。

反之，类似二项式反演的式子，也可以 $O(n \log n)$ 求出 $0 \sim n$ 的点值。

FFT 循环卷积

f^{m} mod (f^{n} - 1) = f^{m mod n}

$f^m \bmod (f^n - 1) = f^{m \bmod n}$

也就说如果空间没有开够，那么溢出的贡献不会消失，而是转移到最前面。

减法卷积 优化时空常数。

对于：

h_{i} = \sum_{j = 0}^{n} f_{j} g_{i + j}

$h_i = \sum_{j = 0}^n f_j g_{i + j}$

翻转 $f$ 有：

h_{i} = \sum_{j = 0}^{n} f_{n - j} g_{i + j}

$h_i = \sum_{j = 0}^n f_{n - j} g_{i + j}$

发现， $h_i$ 实际上是得出卷积的第 $i + n$ 项。

如果取长度 $2n$ ，溢出的部分贡献到 $[0, n)$ ，不会对 $[n, 2n)$ 造成影响，所以可以放心大胆的溢出。

常数优化 $\frac 23$ 。

关于位运算的一些性质/套路

异或

异或存在 $x ~\^~~ y \le x + y$ 的性质，这意味这有些时候异或可以因此而贪心的求解。
异或的每一位是独立的，这其实我们可以 $O(\log V)$ 的拆位求贡献，例如在 trie 上求 $\sum x ~\^~~ a_i$ 可以做到时间 $O(\log V)$ 空间 $O(n \log^2 V)$ 。
异或是不进位的加法，如果要同时满足异或和为某个数，并且和为某个数的时候，也可以从高位往低位的填 $0/1$ ，但是此时状态数应该是 $f_{i, j}$ 表示填完了 $i$ 位，还需要进位 $j \times 2^i$ ，转换为下一位就需要 $2j \times 2^{i - 1}$ 也就是进 $2j$ 次了，此时再枚举填了多少个 $1$ （奇数个或者偶数个），可以做到 $O(n \log S)$ ，其中 $n$ 表示数的个数， $S$ 就是要满足的和的大小。参考 [SDOI2019] 移动金币 - 洛谷。
有些时候我们需要求与第 $k$ 小相关的问题，此时我们可能需要二分判断。注意此时可能是 $O(\log^2 V)$ 的，但是可以利用在树上二分来优化一只 $O(\log V)$ ，因为 01trie 和 segment 可以说都是二分自动机。

一般套路

全局异或在 01trie 上的影响只是交换部分层的左右儿子，但是或/与的影响是破坏性的。
- 如果没有修改，那么考虑到破坏性的操作对于每一个 01trie 节点至多破坏一次，那么可以得到一个均摊 $O(n \log V)$ 的操作方式。
- 注意到只有 $O(\log V)$ 层，每层破坏是同时的，那么每新增一层修改就重构整个结构即可，之后的操作都可以转化为 xor, 因为只有一个儿子了。

关于贪心的一些套路

关于加法与乘法的贪心

一般来说，如果贪心与顺序相关，那么加法在乘法前面是最好的（在非负的情况下），指的是： $ax + b < a(x + b)$ 。

类似的，多种操作分别处理是复杂度，考虑可以转化为一类操作，例如乘法。

可以通过贪心的策略对于加法的顺序做限制，例如 CF521D Shop

或者将乘法转化为多次的加法，例如 [CSP-S2020] 函数调用（虽然这不是贪心

关于微扰贪心的证明

参考例题：[yLOI2019] 梅深不见冬 - 洛谷，皇后游戏 - 洛谷，[NOIP2012 提高组] 国王游戏 - 洛谷。其中皇后游戏极其经典。

考虑证明该如何证明，据此看来有两种证明方法：

假定上一个状态固定，考虑这一次先放 $i$ 再放 $j$ 或者反过来的贡献。可能会存在类似于 $\max(last, a) \le \max(last, b)$ 的存在，可以通过分讨，与题意产生神秘的冲突然后消掉。于是可以得到 $a \le b$ 的某种偏序关系。
也可以考虑从 $0$ 开始，也就是没有初始的情况，得到一个结论，然后归纳证明。

这种题该是有比较明显的特征，也就是最小化最后一个值，并且是需要枚举一个排列（代表着朴素的做法为 $O(n!)$ 。所以我们把它变成一种偏序，并以此作为排列依据求出最合理的排列即可。

关于贪心中的反悔自动机

Buy Low Sell High - 洛谷也就是维护反悔答案的插值，从而得到全局最优解。

好吧，本质上就是反悔贪心，只是利用 $\Delta$ 优化了而已 QwQ

关于图论的一些小问题

最短路相关

一般来说，最短路的算法有三：floyd, djk, SPFA，相应的有变形应用。

floyd，可以求与环相关的问题，例如判断最小环长。
djk 常用的写法是记录最近距离对应的点，但是谨记 $O(n^2)$ 本质上是记录的最短的边，而不是点！
SPFA 用来处理有负权的情况。

混合图的欧拉回路

见混合图的欧拉回路 Euler Circuit - 洛谷

存在欧拉回路的条件：对于有向图，每个点出度等于入度。

由于存在双向边，所以考虑 $d_x = in_x - out_x$ ，如果 $d_x \& 1$ 那么一定无解。

欧拉回路实质是出度和入度的转移，故利用网络流求解。

SPFA 判断负环存在性

注意对于一个不存在负环的图，从起点到任意一个点最短距离经过的点最多只有 $n$ 个。

也就是说，一个点的松弛路径最多为 $n$ 。

所以在 SPFA 中可以如此写：

if (dis[y] > dis[x] + w) {
    dis[y] = dis[x] + w;
    if ((cnt[y] = cnt[x] + 1) > n) NEGETIVE_RING!
}

复杂度还是 $O(nm)$ ，但是平均表现好很多。

但是还是不够快，考虑基于 DFS 的 SPFA 判负环，这是相对最快的。

注意初始化时 $dis_x = 0$ ，以及每一个点都需要 DFS 一次！

bool SPFA(int x) {
    vis[x] = true;
    for (auto e : G[x]) {
        if (dis[e.to] > dis[x] + e.w) {
            dis[e.to] = dis[x] + e.w;
            if (vis[e.to]) {
                vis[e.to] = false; return true;
            } else if (SPFA(e.to, mid)) {
                vis[e.to] = false; return true;
            }
        }
    }

    return vis[x] = false;
}

bool check() {
    fill(dis + 1, dis + 1 + n, 0);
    for (int i = 1; i <= n; ++i)
        if (SPFA(i)) return true;
    return false;
}

平面图的一些性质

平面图中所有面的次数之和等于边数 $m$ 的 $2$ 倍。

平面图的每一个面对应着对偶图的每一个点。欧拉公式说的是 $n - m + r = 2$ ，其中 $r$ 为面数。

平面图的对偶图也是平面图，自环对应其中的桥。

关于网络流与贪心

网络流本质上是一种对于流量的反悔贪心，所以如果可以网络流建模，那么可以考虑如下思路：

利用题目特殊性质模拟网络流（利用最小割）/费用流
反悔贪心

在二分图上很有用。

网络流动态加边问题

在二分图上动态加边匹配可以利用匈牙利算法完成，本质是反悔贪心，一般来说是 $O(n m^2)$ 的。

如果利用网络流，每次在残量网络上增广，那么复杂度还是 $O(n m^2)$ 的。

但是如果存在 $n < m$ ，那么考虑可以将复杂度优化为 $O(n m f(n))$ ，其中 $f(n)$ 是最大流。

考虑在二分图匹配中，边权为 $1$ ，每次增广是 $O(m)$ ，但是流至少增加 $1$ ，所以是 $O(nmf(n))$ 的，但是想要复杂度不写假有点复杂……所以一般来说利用这个思路剪枝即可，看出题人是否毒瘤。

各种神秘的等式

二分图最大匹配 $=$ 最大边独立 $=$ 最小点覆盖 $= n -$ 最大点独立 $= n -$ 最小边覆盖
最大团 $=$ 补图的最大独立集
DAG 的不可重最小路径覆盖 $= n -$ 入度出度二分图最大匹配。
DAG 的最大独立集 $=$ 最长反链 $=$ 最小可重路径覆盖 = 传递闭包后的不可重最小路径覆盖
平面图最大流 $=$ 平面图最小割 $=$ 对偶图最短路

关于多状态 $O(n)$ 单次求解问题的优化方法

原未精简内容在注释中。

一般来说可以有下列套路，但是都是基于重复利用信息的思想，符合算法优化的本质

分治，无论是 $[l, mid)$ 和 $[mid, r)$ 的分治，还是矩形减半的分治，还是 CDQ 分治。
撒点，调和级数的枚举长度区间，考虑合并 $(i - len, i], [i, i + len)$ 的贡献，类似 NOI 优秀的拆分的做法
扫描线，不断移动一个端点，然后利用某个性质更新左半边的信息。
直接优化 $O(n)$ 求解的复杂度，通过预处理的变为 $O(\log n)$ 甚至 $O(1)$ 的，一般配合倍增使用。
枚举每一个点，求其贡献的次数，例如 CSP2019 树的重心

扫描线的一些套路

枚举每一个点，不仅仅是可以枚举序列上的每一个元素，也可以枚举每一种元素，例如【美团杯2021】A. 数据结构，考虑每一种颜色对于答案的影响。

考虑容斥，或者反演，利用其它的信息间接的快速求出想要的信息，例如 HDU5603。

区间的子区间，例如 P8868 [NOIP2022] 比赛，转化为 2-side 问题。

关于换维扫描线

利用这个套路想出了三道题了！

其处理的修改与询问大概类如：

通过换维扫描线使得：

区间加 $\to$ 单点加
单点查 $\to$ 区间查

通俗一点来说，就是对于修改建立数据结构！

关于并查集维护关系 - 扩展域并查集

关系，例如食物链的关系，同类，猎物。

认为有三种角色，自己，猎物，天敌，分别维护 是 的关系即可。

扩展出来，发现对于关系，找出链循环长度，维护长度个并查集即可。

相等和不等关系（ $01$ ）异或关系也可以类比维护。

关于撤销结构均摊复杂度

如果要求维护一个线性结构，支持在末尾插入或删除，在开头删除，动态维护其最大值，该如何做？

一个 naive 的想法是类似 ST 表的操作，可以做到 $O(\log n)$ 插入， $O(1)$ 查询和删除，但是还是不够，如果做到 $O(1)$ 完成所有操作，考虑如果不在开头删除时简单的，所以把整个序列分成两个栈（原本是一个队列），分别维护前后缀和，利用核算法可以分析出其是线性的，只是常数略大。

关于线段区间赋值的问题

TNND，赋值后的修改注意需要对于 ass[p] 标记生效！

恶臭的代码，满文的 ass……
但是因此我错了好几次了！大大的注意！

或者说，可以利用矩阵进行简化，例如 P8476 「GLR-R3」惊蛰的代码。

关于因数相关量的上界

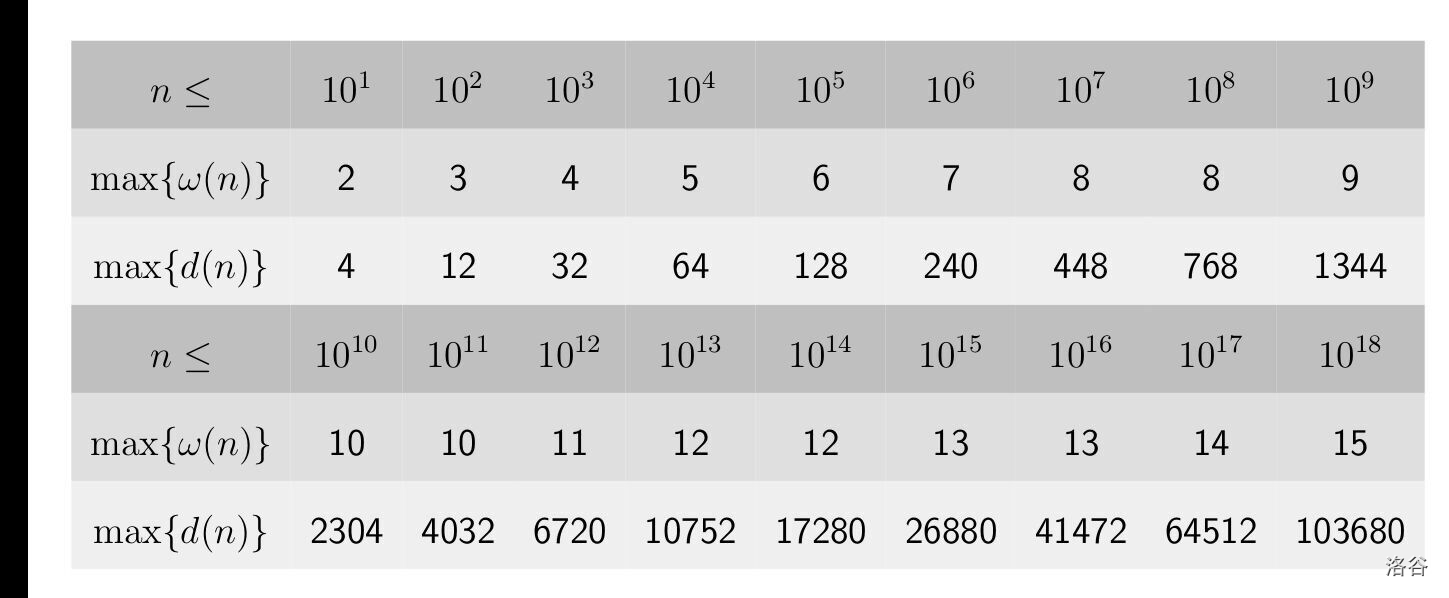
有些与因数个数相关的题目可以借此保证复杂度，例如 [1900D - Small GCD](https://codeforces.com/problemset/problem/1900/D

关于区间众数或绝对众数

区间众数是困难的，离线可以利用回滚莫队完成，在线可以利用分块完成。

但是绝对众数是简单的，这里有两个套路：

摩尔投票法（票子多了不起！
二进制拆分

摩尔投票与序列顺序无关，所以可以利用线段树维护结构 {val, cnt}，合并是简单的。

例题：[NOI2022] 众数

摩尔投票是常用的，但是二进制拆分。

考虑求绝对众数最暴力的算法是开一个桶记录个数，类似 radix sort 的思路，按照进制划分组，那么绝对众数一定是组内最多的那个，考虑二进制拆分即可。可以利用 $4, 8, 16$ 进制优化常数，但是最后还是需要一次数点判断到底是否正确。

posted @ 2023-08-17 10:27 jeefy 阅读(177) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· CF题解合集

· 算法学习笔记(17): 快速傅里叶变换（FFT）

· OI-Wiki 学习笔记

· UOJ随做

· 杂题选写3

阅读排行：
· DeepSeek 开源周回顾「GitHub 热点速览」
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· .NET 10首个预览版发布：重大改进与新特性概览！
· AI与.NET技术实操系列（二）：开始使用ML.NET
· 单线程的Redis速度为什么快？

公告

昵称： jeefy
园龄： 2年1个月
粉丝： 32
关注： 13

+加关注

2025年3月

日

一

二

三

四

五

六

jeefy

信仰，梦想，希望！