算法学习笔记(27): 后缀结构
本文不宜初学用。
后缀排序
开篇膜拜 Pecco：算法学习笔记(84): 后缀数组 - 知乎 (zhihu.com)
有些时候，其实 \(O(n \log^2 n)\) 的排序也挺好。又短又简单。
其中 \(rk[i]\) 表示从第 \(i\) 个字符开始的后缀的排名，\(sa[i]\) 表示排名为 \(i\) 的后缀开始的位置。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
const int N = 1e6 + 7;
char s[N];
int n;
int SA[N << 1], temp[2][N << 1];
void getSA() {
for (int i(0); i < n; ++i) SA[i] = i, temp[0][i] = s[i];
for (int w(1), k(0); w < n; w <<= 1, k ^= 1) {
int *rank = temp[k], *backup = temp[k ^ 1];
std::sort(SA, SA + n, [&](const int &x, const int &y) {
return rank[x] ^ rank[y] ? rank[x] < rank[y] : rank[x + w] < rank[y + w];
});
for (int p(1), i(0); i < n; ++i) {
backup[SA[i]] = (rank[SA[i]] == rank[SA[i + 1]] && rank[SA[i] + w] == rank[SA[i + 1] + w]) ? p : p++;
}
}
}
那么接下来考虑利用基数排序优化一个 \(\log n\)。
其本质是按照上一次的 \(rk[i]\) 为第一关键字， \(rk[i + w]\) 为第二关键字排序。
而排序之后，其 \(rk\) 本身就是有序的，所以基数排序按照第二关键字排序的部分可以简化。
直接把后 \(w\) 个提到后面就是了。
然后考虑对于第一关键字桶排序，嗯，看代码。
char s[N];
int sa[N], tmp[2][N], cnt[N]; // cnt 是 radix_sort的计数桶
int * getSA(int n) {
int m = 128; // 值域
int *x = tmp[0], *y = tmp[1];
// 第一次排序
for (int i = 1; i <= n; ++i)
++cnt[x[i] = s[i]];
// 计数前缀和
for (int i = 1; i <= m; ++i)
cnt[i] += cnt[i - 1];
for (int i = n; i; --i)
sa[cnt[x[i]]--] = i;
// 开始之后的排序，对于 (rank[x], rank[x + k]) 进行排序。
for (int p, k = 1; k < n; k <<= 1) {
p = 0;
// 由于对于 [n - k + 1, n]，其 rank[x + k] 一定为0，故会被放在最前面
for (int i = n - k + 1; i <= n; ++i) y[++p] = i;
// 很明显，rk已经是有序的，前k名一定是已经被放入的(rank[x+k] = 0)
// 所以，我们只需要将后面的 n-k 个按顺序加入即可
// （对于此次的第二关键词排序即使对上一次的第一关键词排序，已经是有序的，所以直接加进去）
for (int i = 1; i <= n; ++i) {
if (sa[i] > k) y[++p] = sa[i] - k;
}
// 现在开始对于第一关键字排序
// 清空计数桶，实际上可能不需要？
for (int i = 0; i <= m; ++i) cnt[i] = 0;
// x[i] 实际上就是上一次的rank，也就是第一关键字
// 实际上这里可以写作 ++cnt[x[y[i]]]; 效果是一样的
for (int i = 1; i <= n; ++i) ++cnt[x[i]];
for (int i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
// i外套了一层y[i], 实际上就是按照第二关键词排好的顺序放回原数组中。
for (int i = n; i; --i)
sa[cnt[x[y[i]]]--] = y[i], y[i] = 0;
// 为了避免memset，类似于滚动数组的思想
swap(x, y);
// 此时y也就是之前的rank，那么我们现在要取得此时的rank
p = 0;
for (int i = 1; i <= n; ++i) {
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? p : ++p;
}
if (p >= n) break; // 完成排序，每一个都不一样了。
m = p; // 改变值域，最终为n
}
return x; // 最终的rank
}
如果不愿意这么复杂，那么这里提供一种 \(20\) 行搞定的简单的写法（虽然常数略大，在 \(10^6\) 的数据下有 \(5\) 倍差距……）
int sa[N], _mem[2][N], *rk = _mem[0], *tmp = _mem[1], cnt[N];
void SuffixSort(int n, const string &s) {
#define radixSort(v, w, u) {\
for (register int i = 1; i <= n; ++i) ++cnt[rk[i + w]]; \
for (register int i = 1; i <= u; ++i) cnt[i] += cnt[i - 1]; \
for (register int i = n; i >= 1; --i) tmp[cnt[rk[v[i] + w]]--] = v[i]; \
for (register int i = 0; i <= u; ++i) cnt[i] = 0; \
for (register int i = 1; i <= n; ++i) v[i] = tmp[i]; \
};
for (int i = 1; i <= n; ++i) sa[i] = i, rk[i] = s[i - 1];
int m = 128;
for (int w = 1, i, p; w <= n; w <<= 1) {
radixSort(sa, w, m);
radixSort(sa, 0, m);
for (p = 1, i = 1; i <= n; ++i) {
tmp[sa[i]] = (rk[sa[i]] == rk[sa[i + 1]] && rk[sa[i] + w] == rk[sa[i + 1] + w])
? p : p++;
} m = p, swap(tmp, rk);
}
}
LCP
观察排序后的字符串：
来自 Pecco 大佬。
可以看到，相邻的后缀之间可能有一些共同前缀。
那么我们可以利用后缀数组找出 Longest Common Prefix，也就是所谓的 LCP。
假设 \(H[i] = lcp(sa[i], sa[i - 1])\)。
以及 \(h[i] = H[rk[i]]\)。
有定理 \(h[i] \ge h[i - 1] - 1\)。
其文本理解为：对于后缀 \(i\)，与字典序在其前面一个的后缀的的最长公共前缀的长度，大于上一个后缀与其字典序前一个后缀的LCP减一。
还是很抽象……证明来自 OI wiki
于是我们可以 \(O(n)\) 的求出 \(H\) 数组了。
void getHt(int n) {
for (int i = 1, k = 0; i <= n; ++i) {
if (k > 0) --k;
while (s[i + k] == s[sa[rk[i] - 1] + k])
++k;
H[rk[i]] = k;
}
}
求一个字符串的本质不同子串个数就可以利用 \(H\)。
其式子为：
测试：不同子串个数 - 洛谷
求两个串 \(i, j\) 的最长公共前缀。
利用 \(H\) 转化为 RMQ 问题
\(\to lcp(i, j) = \min_{k = rk[i] + 1}^{rk[j]} H[i]\)
感性理解为字典序上相差越大，相同越小。如此而已。
其实感觉这个没啥用，完全可以被哈希二分水过，而且时空常数还小很多……
题目：最长公共前缀 - 洛谷
哈希第 \(k\) 大。
现在我还只会不同位置的相同子串算作一个的情况。
按照 \(sa[i]\) 中的东西向后，每一个子串对字典序的贡献为 \(n - sa[i] + 1 - H[i]\)。
所以依次遍历就是了。
for (int i = 1; i <= n; ++i) {
int difc = n - sa[i] + 1 - H[i];
if (k > difc) {
k -= difc; continue;
}
for (int j = sa[i]; j <= sa[i] + k + H[i] - 1; ++j)
putchar(A[j - 1]);
k = 0;
}
if (k > 0) puts("-1");
见：[HEOI2016/TJOI2016] 字符串 - 洛谷
考察的是后缀数组的综合应用：直接求不好求，转化为判断 \(s[c..d]\) 的某个前缀是否在 \(s[a..b]\) 中出现过。
其满足单调性，所以二分 \(mid\)，但是如何判断？发现合法的后缀 \(S\) 限制有二：
-
开头在 \([c, d - mid + 1]\) 中
-
\(lcp(S, c) \ge mid\)
第二部分在 SA 数组上一定满足时连续的一段区间，这部分可以二分出来。
不过需要通过 ST 表来优化查询，使之为 \(O(\log n)\)。
那么判断满足第一个条件，就可以利用一个主席树上二分找了。
主席树上 \(i\) 对应的在 \(sa_i\) 处 \(+1\)，查询时差分求个数即是。
最后外面套了一层二分，所以整体的复杂度是 \(O(n \log n + q \log^2 n)\)，倒是不怎么卡常，只是代码很难受，需要对这些东西十分的熟练才可以很快的写出来。
后缀自动姬
时间和精力原因，原理部分不会展开。
struct SAM {
int ch[N][26], link[N], len[N], use = 1, last = 1;
void extend(int c) {
int p = last, now = last = ++use;
len[now] = len[p] + 1;
while (p && !ch[p][c]) ch[p][c] = now, p = link[p];
if (!p) return (void)(link[now] = 1);
int q = ch[p][c];
if (len[q] == len[p] + 1) return (void)(link[now] = q);
int crt = ++use;
len[crt] = len[p] + 1;
link[crt] = link[q], copy_n(ch[q], 26, ch[crt]);
link[q] = link[now] = crt;
while (p && ch[p][c] == q) ch[p][c] = crt, p = link[p];
}
int buc[N], ord[N], cnt[N];
void sort() {
int V = 1;
for (int i = 1; i <= use; ++i) V = max(V, len[i]), ++cnt[len[i]];
for (int i = 1; i <= V; ++i) cnt[i] += cnt[i - 1];
for (int i = use; i; --i) ord[cnt[len[i]]--] = i;
}
int calc() {
for (int i = use; i; --i) {
int x = ord[i];
// do something with x...
}
}
}
总结一点个人易错的点：
extend中link[now] = 1/q容易写成link[p] = 1/q。- 其中
link[q] = link[now] = crt容易写成link[crt] = link[now] = q calc部分容易直接把 \(i\) 当 \(x\) 使用，出现玄妙错误。
对于字符串 \(S\) 建出来的后缀自动机是个什么东西？
对于 link 会建出来一棵 parent tree，每个节点实际上代表了一个子串集合，对于这个集合内的串，出现位置的末尾集合是相同的，这个位置集合就是 \(\rm endpos\) 集合。
对于 \(x\) 和 \(y = link_x\)，满足 \({\rm endpos}_x \subset {\rm endpos}_y\)。注意是真子集。
并且对于 \(x\) 的所有儿子，满足 \({\rm endpos}_x = \bigcup_{y \in Son(x)} {\rm endpos}_y\)，并且儿子间集合两两无交。
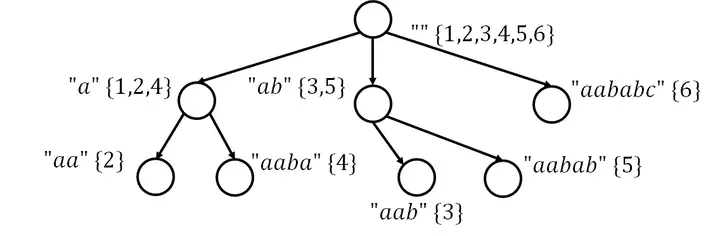
借用 @pecco 的图，对于字符串 aababc 的 parent tree 如上图。
一般我们对于这个集合有两种基本应用：大小，其内元素。
如果只需要大小，每次插入字符新建节点时，注意到其一定唯一，也就是 \(|{\rm endpos}| = 1\)，相当于知道了叶子节点的位置。那么最后只需要按照拓扑序合并即可。
而欲知道其内有哪些，类似也知道 \(|{\rm endpos}| = 1\) 时唯一的位置是哪一个，然后拓扑序合并即可。一般来说，利用可持久化线段树合并实现，时空均为 \(O(n \log n)\)，并且可以知道每一个节点的元素。
对于 ch 会建出来一个自动机。将一个串 \(T\) 放入这个自动机上转移，如果到了 \(T_i\) 无法转移，那么说明 \(T_{[0, i)}\) 是 \(S\) 的一个子串，而 \(T_{[0, i]}\) 则不是。这里 \(i\) 是最大的，也就是求出了一个最长前缀满足是 \(S\) 的子串；同时，在最后一个节点上，我们可以通过 \(\rm endpos\) 知道其出现了多少次，出现在哪里。
自然的需要思考是否可以求出 \(T\) 和 \(S\) 的最长公共子串？一个暴力的想法是把 \(T\) 的每一个前缀都放进去跑，但是显然不够优秀。考虑到 parent tree 另一个重要的性质，对于 \(x\) 和 \(y = link_x\)，\(y\) 代表的字符串一定是 \(x\) 代表的串的后缀。于是当无法转移的时候，不断跳 \(link\) 并且更新长度即可。
- 求 \(S\) 的最小表示法（循环同构字符串中字典序最小的一个）
非常高级，对于 \(S + S\) 建出 SAM，然后每次走字典序最小的那个转移，走 \(|S|\) 步即可。
类似的问题，求 \(S\) 循环同构中字典序第 \(k\) 大的是谁，记搜一下之后还可以产生多少种可行，但是复杂度可能不是很对，因为一个节点对应的长度不止一种。但是用 SA 是挺简单的，\(O(n \log n)\) 预处理，然后从后向前扫扫即可。
- 求 \(S\) 的子串中字典序第 \(k\) 大。
如果是本质不同的子串中字典序第 \(k\) 大，那么用 SA 是简单的。
但是如果不是，那么利用 SAM，还是预处理出每次转移到的状态之后能够转移到多少种状态，注意每个节点初始值是 \(|{\rm endpos}|\)，跑一遍拓扑即可求出状态数。然后 dfs 即可。
- 求多个串的最长公共子串
考虑两个串的最长公共子串我们得到的东西。对于 \(S\)，我们得到了每一个 \(\rm endpos\) 集合和 \(T\) 最长的匹配长度（实际上有 \(O(|T|)\) 次子树取 \(\max\)，这在最后可以 \(O(|S|)\) 的处理）。同理，可以得到其他所有串的最长匹配长度。那么只需要对于每一个 \(\rm endpos\) 所有匹配长度取 \(\min\)，然后所有节点取 \(\max\) 即可。
必须要用最短的那个串建立 SAM，因为这里单次的复杂度是 \(O(|S| + |T|)\) 的，这样才能保证复杂度还是 \(O(\sum |S_i|)\) 的。
不过可以用广义后缀自动机完成，其复杂度略劣。是 \(O(n |S|)\) 的，还有一种实现是 \(O(|S| + n \log n)\) 的，似乎很没有必要，并且如果是要计数的话可能还是只能 \(O(n |S|)\)。
广义后缀自动机
就是先把 trie 建出来，然后 bfs 建 SAM。在线的话建 SAM 的 insert 部分需要修改，但是应该没有什么特别大的用。
那么在其上的用法实际上和正常的后缀自动机应当是没有太大的区别的。
但是看到网上说，sort 部分不应该直接按照 len 排序，因为这是广义 sam，需要真正的跑一次拓扑排序。原因不太清楚，待补。
