算法学习笔记(23): 马尔可夫链中的期望问题

合集 - 算法学习笔记(52)

29.算法学习笔记(23): 马尔可夫链中的期望问题2023-06-01

马尔可夫链中的期望问题

这个问题是我在做 [ZJOI2013] 抛硬币 - 洛谷这道题的时候了解的一个概念。

在网上也只找到了一篇相关的内容：# 马尔可夫链中的期望问题

故在这里来分享一下其中的期望问题。

马尔可夫链中的期望问题

马尔可夫链

定义：马尔科夫链为状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备“无记忆性”，也就是说当前状态的概率仅与上一个状态相关。

数学定义：假定我们的序列状态为 $\dots, X_{t-2}, X_{t-1}, X_t, X_{t+1}, X_{t+2}, \dots$ ，那么在 $X_{t+1}$

时刻的状态的条件概率仅依赖于前一刻的状态 $X_t$ ，即：

P (X_{t + 1} | . . ., X_{t - 2}, X_{t - 1}, X_{t}) = P (X_{t + 1} | X_{t})

$P(X_{t+1}| ..., X_{t-2}, X_{t-1}, X_t) = P(X_{t+1} | X_t)$

既然某一时刻状态转移的概率只依赖于它的前一个状态 ，那么我们只要能求出系统中任意两个状态之间的转换概率，这个马尔科夫链的模型就定了。

概率转移矩阵

通过马尔科夫链的模型转换，我们可以将事件的状态转换成概率矩阵 （又称状态分布矩阵 ），如下例：

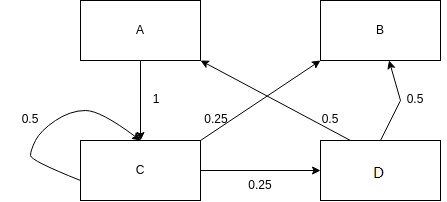
其中线上的数字表示是状态转移到另一状态的概率

那么我们可以构造出如下矩阵：

P = (\begin{matrix} A & B & C & D \\ A & 0 & 0 & 0 & 0.5 \\ B & 0 & 0 & 0.25 & 0.5 \\ C & 1 & 0 & 0.5 & 0 \\ D & 0 & 0 & 0.25 & 0 \end{matrix})

$P = \begin{pmatrix} & A & B & C & D \\ A & 0 & 0 & 0 & 0.5 \\ B & 0 & 0 & 0.25 & 0.5 \\ C & 1 & 0 & 0.5 & 0 \\ D & 0 & 0 & 0.25 & 0 \end{pmatrix}$

假定我们初始状态为 $A$ ，于是状态矩阵可以定义为

S = (\begin{matrix} 1 \\ 0 \\ 0 \\ 0 \end{matrix})

$S = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}$

那么经过 $k$ 次转移后的概率分布是什么？

S_{k} = P^{k} S

$S_k = P^kS$

例如 $k = 4$ 时

S_{4} = (\begin{matrix} 0.0625 \\ 0.125 \\ 0.25 \\ 0.0625 \end{matrix})

$S_4 = \begin{pmatrix} 0.0625 \\ 0.125 \\ 0.25 \\ 0.0625 \end{pmatrix}$

通过 numpy 计算：

s = np.array([[1], [0], [0], [0]])
P = np.array([
      [0, 0, 0, 0.5],
      [0, 0, 0.25, 0.5],
      [1, 0, 0.5, 0],
      [0, 0, 0.25, 0]
])
i, n = 0, 4
while i < n:
    s = P.dot(s)
    i = i + 1
print(s)

转移矩阵的修订

如果我们到达了某一个点就结束了整个过程，那么我们需要对状态转移做一定的更改：

呃，这部分对于本文似乎有一点偏题了……请适当略过

我们新增了一个节点，将所有转移到 $B$ 的状态转移为最终状态，也就是对于 $B$ 的状态累计求和。

于是新的矩阵成为：

s = np.array([[1], [0], [0], [0], [0]])
P = np.array([
      [0, 0, 0, 0.5, 0],
      [0, 0, 0.25, 0.5, 0],
      [1, 0, 0.5, 0, 0], 
      [0, 0, 0.25, 0, 0], 
      [0, 1, 0, 0, 1]
])

最终 $S_k = P^kS$ 就是积累后的概率矩阵。

状态中的期望

我们关注的是到达状态 $B$ 所需要的平均转移次数，所以我们把随机变量 $X$ 看作到达目标状态所需要的步数。

根据变量期望的定义可得：

E (X) = \sum_{k = 1}^{\infty} [k \cdot P (X = k)]

$E(X) = \sum_{k = 1}^{\infty} [k \cdot P(X = k)]$

那么现在的问题就变为了求 $P(X = k)$ 。

根据上文， $P(X = k) = [B]S_k = [B]P^kS$ ，也就是取 $S_k$ 与 $B$ 相关的那一项。

或许我们可以求得 $[B]S_k$ 的通项（一个多项式？）从而求得期望。

在顶端链接的文章中提到：

事实上，我们可以计算转移矩阵的 $n$ 次方，即得到各元素关于 $n$ 的表达式.

由于我没有学过线性代数，所以我就不在本文中展开。

而是采用第二种方法：期望线性方程组

期望线性方程组

显然~~至少目前对我而言~~，求通项的方法不可行，所以我们需要利用另外一种方法。

我们仍然求从 $A$ 转移到 $B$ 所需要的平均转移次数。

那么我们不妨设 $E_i$ 表示从状态 $i$ 转移到 $B$ 所需要的期望次数， $p_{ji}$ 表示从状态 $j$ 从 $i$ 转移来的概率。

那么有：

E_{i} = 1 + \sum_{j} p_{j i} \cdot E_{j}

$E_i = 1 + \sum_{j} p_{ji} \cdot E_j$

也就是说 $E_i$ 等于 $i$ 可以直接转移到的状态的期望乘上转移的概率的和再加上 $1$ （转移的代价，1步）

以上文中例子为例，可以列出：

\begin{aligned} E_{A} & = E_{C} + 1 \\ E_{C} & = 0.25 E_{B} + 0.25 E_{D} + 1 \\ E_{D} & = 0.5 E_{A} + 0.5 E_{B} + 1 \end{aligned}

$\begin{aligned} E_A &= E_C + 1 \\ E_C &= 0.25E_B + 0.25E_D + 1 \\ E_D &= 0.5E_A + 0.5E_B + 1\\ \end{aligned}$

而特殊的， $E_B = 0$ ，因为已经到达目标了

而可以解出 $E_A = 4$ 。

也就是说，从 $A$ 转移到 $B$ 的期望步数是 $4$ 。

方程矩阵化

如果我们把列出来的方程看作矩阵，那么可以得到：

P = np.array([
    [0-1, 0, 1, 0],
    [0, 0-1, 0, 0],
    [0, 0.25, 0.5-1, 0.25],
    [0.5, 0.5, 0, 0-1]
])

~~似乎是我原本概率转移矩阵有问题？~~

也就是原概率矩阵的转置矩阵再在对角线上全部减一。

或者可以表示为

P^{'} = P^{T} - I_{n}

$P' = P^T - I_n$

而我们最终求解的方程为：

P^{'} E = (\begin{matrix} - 1 \\ - 1 \\ ⋮ \\ - 1 \end{matrix})

$P'E = \begin{pmatrix} -1 \\ -1 \\ \vdots \\ -1 \end{pmatrix}$

利用~~死去的~~高斯消元即可。

例题

链接：[六省联考 2017] 分手是祝愿 - 洛谷

在题解区中全是某种奇怪的 DP 设计。所以这里来讲述一下利用本文中的方法求解的方法。

最开始的模型转化我们就省略了……

我们设 $E_i$ 表示从剩下 $i$ 个地方没有按下到全部按下的期望步数。

根据题目，我们有：

E_{i} = \frac{i}{n} E_{i - 1} + \frac{n - i}{n} E_{i + 1} + 1

$E_i = \frac in E_{i-1} + \frac {n-i}n E_{i+1} + 1$

并且由于最优限制：

i \leq k ⟺ E_{i} = i

$i \le k \iff E_i = i$

所以我们可以轻易的利用高斯消元求解……但是很明显，这是不现实的……考虑这个矩阵是一个稀疏矩阵，而且每一个方程是只与临近对角线的 3 个元素相关，所以我们可以轻易的将空间优化到 $O(3n)$ 。

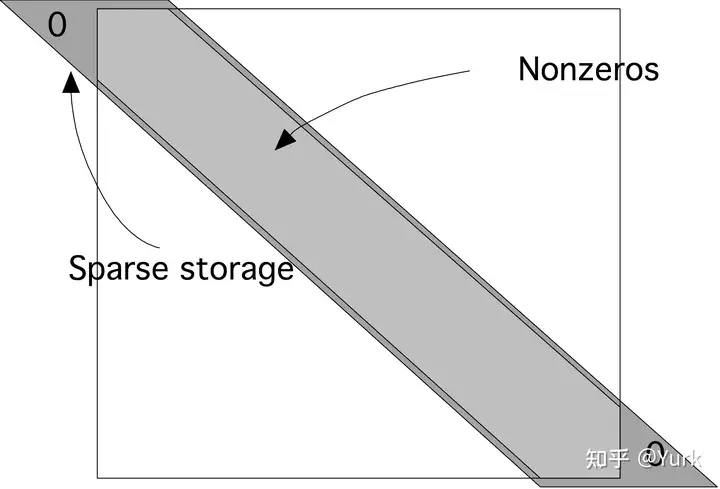
参考至知乎：# 数值线性代数｜LU分解与稀疏矩阵

于是我们可以旋转一下，只存储非0的元素

接下来我们只需要参考 Guass-Jordan 消元法（先从上到下消下三角，再从下到上消上三角）。那么复杂度成功的也被我们降到了 $O(n)$ 。只是常数有点小大……

作者有话说

其实本文讲述的方法存在很大的局限性，尤其的求解的过程，很容易就变成了 $O(n^3)$ 。

不过似乎建模的过程还是蛮简单的？

在求期望的问题中，这不失为一个思考的方向。有些时候，可以通过题目相关的特殊性质进行优化，使得复杂度降低。

可是毒瘤出题人们……还是看每道题的正解吧，或许终将有一天，这个方法可以被一种通法优化到 $O(n^2)$ 呢？

posted @ 2023-06-01 20:25 jeefy 阅读(1949) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· CF题解合集

· 算法学习笔记(38): 矩阵

· 一道题，一类题

· 应用随机过程02：马尔可夫链及其概率分布

· 算法学习笔记：期望/概率 DP

阅读排行：
· DeepSeek 开源周回顾「GitHub 热点速览」
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· .NET 10首个预览版发布：重大改进与新特性概览！
· AI与.NET技术实操系列（二）：开始使用ML.NET
· 单线程的Redis速度为什么快？

公告

昵称： jeefy
园龄： 2年1个月
粉丝： 32
关注： 13

+加关注

2025年3月

日

一

二

三

四

五

六

jeefy

信仰，梦想，希望！

算法学习笔记(23): 马尔可夫链中的期望问题

马尔可夫链中的期望问题

马尔可夫链

概率转移矩阵

转移矩阵的修订

状态中的期望

期望线性方程组

方程矩阵化

例题

作者有话说

公告

最新随笔

我的标签

合集 (7)

随笔分类 (105)

阅读排行榜

推荐排行榜