算法学习笔记(17): 快速傅里叶变换（FFT）

合集 - 算法学习笔记(52)

1.算法学习笔记(∞)：杂项2023-08-17 2.算法学习笔记(1): 欧几里得算法及其扩展2023-01-12 3.算法学习笔记(2): 欧拉定理与逆元2023-01-13 4.算法学习笔记(3): 倍增2023-01-12 5.算法学习笔记(3.1): ST算法2023-10-13 6.算法学习笔记(4): 并查集及其优化2023-01-12 7.算法学习笔记(5): 最近公共祖先(LCA)2023-01-12 8.算法学习笔记(6): 树链剖分2023-01-12 9.算法学习笔记(7): 二分图2023-01-13 10.算法学习笔记(8): 网络流2023-01-13 11.算法学习笔记(8.0): 网络流前置知识2023-01-13 12.算法学习笔记(8.1): 网络最大流算法 EK, Dinic, ISAP2023-01-14 13.算法学习笔记(8.2): 上下界网络流2023-01-14 14.算法学习笔记(8.3): 网络最大流 - 模型篇2023-12-19 15.算法学习笔记(9): 中国剩余定理(CRT)以及其扩展(EXCRT)2023-01-15 16.算法学习笔记(10): BSGS算法及其扩展算法2023-01-16 17.算法学习笔记(11): 原根2023-01-16 18.算法学习笔记(12): 线性基2023-02-03 19.算法学习笔记(13): Manacher算法2023-02-07 20.算法学习笔记(14): 字符串哈希2023-02-06 21.算法学习笔记(15): Trie（字典树）2023-02-08 22.算法学习笔记(16): 组合数学基础2023-02-08

23.算法学习笔记(17): 快速傅里叶变换（FFT）2023-02-10

快速傅里叶变换（FFT）

有趣啊，都已经到NOI的难度了，救命

快速傅里叶变换（FFT）

首先，我们先讲述一下前置知识。已经明白的读者请移步后文

虚数

定义： $z = a + bi$ ，其中 $a, b \in R\ \ i = \sqrt{-1}$

运算原则：

\begin{aligned} (a + b i) + (c + d i) & = (a + c) + (b + d) i \\ (a + b i) (c + d i) & = (a c - b d) + (a d + b c) i \\ \frac{(a + b i)}{(c + d i)} & = \frac{a c + b d}{c^{2} + d^{2}} + \frac{b c - a d}{c^{2} + d^{2}} \end{aligned}

$\begin{aligned} (a+bi) + (c+di) &= (a+c) + (b+d)i \\ (a+bi)(c+di) &= (ac - bd) + (ad + bc)i \\ \cfrac {(a+bi)}{(c+di)} &= \cfrac {ac + bd}{c^2 + d^2} + \cfrac {bc - ad}{c^2 + d^2} \end{aligned}$

重要性质

e^{i x} = \cos x + i \sin x

$e^{ix} = \cos x + i \sin x$

所以说，一个复数也可以写作 $z = re^{i\theta}$ 的形式。

其中 $r$ 为它的模， $\theta$ 为它的辐角。

于是两个复数相乘也就相当于模相乘，辐角相加：

$z_1 z_2 = r_1r_2 e^{i(\theta_1 + \theta_2)}$

证明：

我们通过欧拉公式在 $0$ 处展开：

\begin{aligned} e^{x} & = 1 + x + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + \dots \\ \cos x & = 1 - \frac{x^{2}}{2!} + \frac{x^{4}}{4!} - \frac{x^{6}}{6!} + \dots \\ \sin x & = x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!} + \dots \end{aligned}

$\begin{aligned} e^x &= 1 + x + \cfrac {x^2}{2!} + \cfrac {x^3}{3!} + \dots \\ \cos x &= 1 - \cfrac {x^2}{2!} + \cfrac {x^4}{4!} - \cfrac {x^6}{6!} + \dots \\ \sin x &= x - \cfrac {x^3}{3!} + \cfrac {x^5}{5!} - \cfrac {x^7}{7!} + \dots \\ \end{aligned}$

那么我们考虑如何把三者扯上关系呢？

由于已知 $i^2 = -1, i^3 = -i$ 那么我们先考虑 $e^{ix}$

e^{i x} = 1 + i x - \frac{x^{2}}{2!} - \frac{i x^{3}}{3!} + \dots

$e^{ix} = 1 + ix - \cfrac {x^2}{2!} - \cfrac {ix^3}{3!} + \dots$

那么，很明显， $e^{ix} = \cos x + i \sin x$

得证。

代码实现

在 C++ 中我们其实可以直接使用 std::complex<double>。

文档可以参考 std::complex - cppreference.com

但是毕竟是 stl，其使用细节肯定没有那么顺手，而且实测很慢，所以建议手写复数模板。

考虑到实际中我们几乎不需要用到除法，所以，我们仅实现三则运算。

struct Complex {
    double real, imag;
    Complex() : real(0), imag(0) {}
    Complex(double re, double im) : real(re), imag(im) {};
    inline Complex operator + (const Complex & b) {
        return Complex(real + b.real, imag + b.imag);
    }
    inline Complex operator - (const Complex & b) {
        return Complex(real - b.real, imag - b.imag);
    }
    inline Complex operator * (const Complex & b) {
        return Complex(real * b.real - imag * b.imag, real * b.imag + imag * b.real);
    }
};

单位根

快速傅里叶变换的核心就是利用的单位根的一些独特的性质来快速实现的

单位根的定义：方程 $z^n = 1$ 在复数范围内的 $n$ 个根。

那么，不经过证明的给出，每一个根应该为 $e^{i\frac{2k\pi}{n}}$ 。

这里我们记 $\omega_n$ 为主 $n$ 次单位根， $\omega_n^k = e^{i\frac{2k\pi}{n}}$

举个例子，主 $8$ 次单位根的 $8$ 个值改写为形如 $(r, \theta)$ 的极坐标后，位置类似于下图：

三个引理

消去定理： $\omega_{dn}^{dk} = \omega_n^k$

证明：考虑展开即可： $\omega_{dn}^{dk} = e^{i\frac{2dk\pi}{dn}} = e^{i\frac{2k\pi}{n}} = w_n^k$

折半引理： $(\omega_n^{k+\frac n2})^2 = (w_n^k)^2 = \omega_{\frac n2}^k$

这个引理是快速傅里叶变化的核心

证明：也是考虑展开

\begin{aligned} ω_{n}^{k + \frac{n}{2}} & = ω_{n}^{k} ω_{n}^{\frac{n}{2}} = - ω_{n}^{k} \\ ↓ \\ (ω_{n}^{k})^{2} & = ω_{n}^{2 k} = ω_{\frac{n}{2}}^{k} \end{aligned}

$\begin{aligned} \omega_n^{k+\frac n2} &= \omega_n^k\omega_n^{\frac n2} = -\omega_n^k \\ &\downarrow \\ (\omega_n^k)^2 &= \omega_n^{2k} = \omega_{\frac n2}^k \end{aligned}$

求和引理： $\sum_{i=0}^{n-1} (\omega_n^k)^i = 0$

证明：

根据等比数列公式

\sum_{i = 0}^{n - 1} (ω_{n}^{k})^{i} = \frac{(w_{n}^{k})^{n} - 1}{w_{n}^{k} - 1} = \frac{(w_{n}^{n})^{k} - 1}{w_{n}^{k} - 1} = \frac{1^{k} - 1}{w_{n}^{k} - 1} = 0

$\sum_{i=0}^{n-1} (\omega_n^k)^i = \cfrac {(w_n^k)^n - 1}{w_n^k - 1} = \cfrac {(w_n^n)^k - 1}{w_n^k - 1} = \cfrac {1^k - 1}{w_n^k - 1} = 0$

得证

多项式

(OI中)一般形式： $F(x) = a_0 + a_1x + a_2 x^2 + \cdots + a_n x^n$

上述多项式为一元多项式。

我们可以改写上式： $\sum_{i=0}^n a_ix^i$

我们对于多项式运算定义如下：

\begin{aligned} A (x) & = \sum_{i = 0}^{n} a_{i} x^{i} \\ B (x) & = \sum_{i = 0}^{n} b_{i} x^{i} \end{aligned}

$\begin{aligned} A(x) &= \sum_{i = 0}^n a_i x^i \\ B(x) &= \sum_{i = 0}^n b_i x^i \\ \end{aligned}$

加法：

A (x) + B (x) = \sum_{i = 0}^{n} (a_{i} + b_{i}) x^{i}

$A(x) + B(x) = \sum_{i = 0}^n (a_i + b_i) x^i$

乘法

一般情况下，我们可以通过补零的方式，将两个次数不同的多项式调整到次数相同。这里我们都补充到 $n$ 的长度

\begin{aligned} c_{i} & = \sum_{j = 0}^{i} a_{j} b_{i - j} \\ A (x) B (x) & = \sum_{i = 0}^{2 n} c_{i} x^{i} \end{aligned}

$\begin{aligned} c_i &= \sum_{j = 0}^{i} a_j b_{i - j} \\ A(x)B(x) &= \sum_{i = 0}^{2n} c_i x^i \\ \end{aligned}$

我们称这个系数向量 $c$ 为向量 $a, b$ 的卷积，记作 $a \otimes b$

表示方法

系数表示

它将一个多项式表示成由其系数构成的向量的形式

例如 $A = [a_0, a_1, a_2, \dots, a_n]^T$

加法即为 $A_1+ A_2$ ，直接相加即可。时间复杂度 $O(n)$

乘法则做向量卷积，为 $A_1 \otimes A_2$ 。一般来说，时间复杂度为 $O(n^2)$

如果给定 $x$ 求值，则可以使用霍纳法则或者秦九昭算法。时间复杂度为 $O(n)$
点值表示

用至少 $n$ 个多项式上的点来表示

一般形式如 $\{(x_0, A(x_0)), (x_1, A(x_1), \dots, (x_n, A(x_n))\}$

进行运算是，一般要保证两个多项式在同一位置取值相同，即 $x_i$ 相同

加法运算直接将两点坐标相加即可，时间复杂度为 $O(n)$

乘法运算只需要将两点纵坐标相乘即可。时间复杂度为 $O(n)$ ，太好了！

如果我们需要 $A(x)$ ，这个过程叫做插值，可以通过拉格朗日插值公式进行计算，复杂度为 $O(n^2)$ ，这里不展开讲述。

离散傅里叶变换(DFT)

DFT(Discrete Fourier Transform) 是快速傅里叶变换（FFT）的基础，也是快速数论变换（NTT）的基础

变换操作是对于一个向量而言（也就是多项式的系数表示法）

这个变换操作相当于求出这个多项式在 $x$ 为单位根时的取值。

不妨设这个向量为 $C = [c_0, c_1, c_2, \dots, c_{n-1}]^T$

我们定义一个变换公式为

h (x) = \sum_{i = 0}^{n - 1} c_{i} x^{i}

$h(x) = \sum_{i = 0}^{n-1}c_i x^i$

那么变换过后的序列为

[h (ω^{0}), h (ω^{1}), h (ω^{2}), \dots, h (ω^{n - 1})]^{T}

$[\ h(\omega^0), h(\omega^1), h(\omega^2), \dots, h(\omega^{n-1})\ ]^T$

其中 $\omega$ 代表主 $n$ 次的单位根。

或者我们可以通过矩阵来表示：

[\begin{matrix} h (ω^{0}) \\ h (ω^{1}) \\ h (ω^{2}) \\ ⋮ \\ h (ω^{n - 1}) \end{matrix}] = [\begin{matrix} 1 & 1 & 1 & 1 & \dots & 1 \\ 1 & ω_{n}^{1} & ω_{n}^{2} & w_{n}^{3} & \dots & ω_{n}^{n - 1} \\ 1 & ω_{n}^{2} & ω_{n}^{2 \times 2} & ω_{n}^{2 \times 3} & \dots & ω_{n}^{2 \times (n - 1)} \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋱ & \dots \\ 1 & ω_{n}^{(n - 1) \times 2} & ω_{n}^{(n - 1) \times 3} & ω_{n}^{(n - 1) \times 2} & \dots & ω_{n}^{(n - 1) \times (n - 1)} \end{matrix}] [\begin{matrix} c_{0} \\ c_{1} \\ c_{2} \\ ⋮ \\ c_{n - 1} \end{matrix}]

$\begin{bmatrix} h(\omega^0) \\ h(\omega^1) \\ h(\omega^2) \\ \vdots \\ h(\omega^{n-1}) \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n^1 & \omega_n^2 & w_n^3 & \cdots & \omega_n^{n-1} \\ 1 & \omega_n^2 & \omega_n^{2\times2} & \omega_n^{2\times3} & \cdots & \omega_n^{2\times(n-1)}\\ \vdots & \vdots & \vdots & \vdots & \ddots & \cdots \\ 1 & \omega_n^{(n-1)\times2} & \omega_n^{(n-1)\times3} & \omega_n^{(n-1)\times2} & \cdots & \omega_n^{(n-1)\times(n-1)} \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \\ c_2 \\ \vdots \\ c_{n-1} \end{bmatrix}$

所以说，暴力的算法为 $O(n^2)$ ，不如直接算。

值得一提的是这个矩阵是范德蒙德方阵，具有非常良好的性质。

对于上述序列，我们称形如 $h(\omega^k)$ 的项为 $k$ 次离散傅里叶级数。

我们将每一项展开，那么可以得到下图：

图片来自网络

这个时候，我们变换后的序列就是用点值表示的序列。

两个变换后的序列相乘，一一对应的乘法即可。

为什么？

变换后的序列其实就是函数在 $w^0, w^1, \cdots , w^{n-1}$ 的点上的取值。

那么根据点值表示的多项式，两个多项式相乘，即是对应点相乘。

于是得到了两个多项式乘积的点值表示。

换句话来说，DFT 实际上所做的事情是插值，同理，IDFT 也相当于插值回去。

离散傅里叶逆变换（IDFT）

我们声称对于上述序列，其 $-k$ 次离散傅里叶变换后的的值恰为 $n \times c_k$ 。

证明：

我们用 $g(\omega^{-k})$ 表示变换后的结果

\begin{aligned} g (ω^{- k}) & = h (ω^{0}) ω^{- 0 k} + h (ω_{1}) ω^{- k} + h (w_{2}) ω^{- 2 k} + \dots + h (ω^{n - 1}) ω^{- (n - 1) k} \\ = \sum_{i = 0}^{n - 1} h (ω^{i}) ω^{- i k} \\ = \sum_{i = 0}^{n - 1} ω^{- i k} \sum_{j = 0}^{n - 1} c_{j} ω^{i j} \\ = \sum_{i = 0}^{n - 1} \sum_{j = 0}^{n - 1} ω^{(j - k) i} c_{j} \\ = \sum_{i = 0}^{n - 1} c_{j} \sum_{j = 0}^{n - 1} ω^{(j - k) i} \end{aligned}

$\begin{aligned} g(\omega^{-k}) &= h(\omega^0) \omega^{-0k} + h(\omega_1) \omega^{-k} + h(w_2) \omega^{-2k} + \cdots + h(\omega^{n-1}) \omega^{-(n-1)k} \\ &= \sum_{i=0}^{n-1} h(\omega^i)\omega^{-ik} \\ &= \sum_{i=0}^{n-1} \omega^{-ik} \sum_{j = 0}^{n-1} c_j \omega^{ij} \\ &= \sum_{i=0}^{n-1} \sum_{j=0}^{n-1} \omega^{(j-k)i} c_j \\ &= \sum_{i=0}^{n-1} c_j \sum_{j=0}^{n-1} \omega^{(j-k)i} \end{aligned}$

我们分类讨论一下：

$j = k$ ，那么此时 $\sum_{j=0}^{n-1} \omega^{(j-k)y} = \sum_{j=0}^{n-1} \omega^0 = n$ 。对于 $c_k$ 做出的贡献为 $n$
$j \ne k$ ，将 $k$ 看作常数，那么此时 $\sum_{j=0}^{n-1} \omega^{(j-k)i} = \sum_{j=0}^{n-1} \omega^{j}$ 。依据上文中求和引理，其值为 $0$ ，也就是对 $c_j$ 做出的贡献为 $0$ 。

综上所述，只有 $c_k$ 对于答案做出了 $n$ 次贡献，所以 $g(\omega^{-k}) = n \times c_k$

此部分到横线分割前可以适当的略过。

观察我们实际上做的事情：

[\begin{matrix} c_{0} \\ c_{1} \\ c_{2} \\ ⋮ \\ c_{n - 1} \end{matrix}] = {[\begin{matrix} 1 & 1 & 1 & 1 & \dots & 1 \\ 1 & ω_{n}^{1} & ω_{n}^{2} & w_{n}^{3} & \dots & ω_{n}^{n - 1} \\ 1 & ω_{n}^{2} & ω_{n}^{2 \times 2} & ω_{n}^{2 \times 3} & \dots & ω_{n}^{2 \times (n - 1)} \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋱ & \dots \\ 1 & ω_{n}^{(n - 1) \times 2} & ω_{n}^{(n - 1) \times 3} & ω_{n}^{(n - 1) \times 2} & \dots & ω_{n}^{(n - 1) \times (n - 1)} \end{matrix}]}^{- 1} [\begin{matrix} h (ω^{0}) \\ h (ω^{1}) \\ h (ω^{2}) \\ ⋮ \\ h (ω^{n - 1}) \end{matrix}]

$\begin{bmatrix} c_0 \\ c_1 \\ c_2 \\ \vdots \\ c_{n-1} \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n^1 & \omega_n^2 & w_n^3 & \cdots & \omega_n^{n-1} \\ 1 & \omega_n^2 & \omega_n^{2\times2} & \omega_n^{2\times3} & \cdots & \omega_n^{2\times(n-1)}\\ \vdots & \vdots & \vdots & \vdots & \ddots & \cdots \\ 1 & \omega_n^{(n-1)\times2} & \omega_n^{(n-1)\times3} & \omega_n^{(n-1)\times2} & \cdots & \omega_n^{(n-1)\times(n-1)} \end{bmatrix}^{-1} \begin{bmatrix} h(\omega^0) \\ h(\omega^1) \\ h(\omega^2) \\ \vdots \\ h(\omega^{n-1}) \end{bmatrix}$

是对于单位根的这个范德蒙德矩阵求逆后于原向量相乘。

我们可以直接对其求逆得到上述结论。

重新审视方阵，发现乘上一个范德蒙德方阵相当于带进了 $n$ 个点进行求值，那么乘上其逆矩阵就应该是用 $n$ 个点插值。

考虑拉格朗日插值：

f (x) = \sum y_{i} \prod_{j \neq i} \frac{x - x_{j}}{x_{i} - x_{j}}

$f(x) = \sum y_i \prod_{j \ne i} \frac {x - x_j} {x_i - x_j}$

比较显然的是：

(V^{- 1})_{i, k} = [x^{k}] \prod_{j \neq i} \frac{x - x_{j}}{x_{i} - x_{j}}

$(V^{-1})_{i, k} = [x^k] \prod_{j \ne i} \frac {x - x_j} {x_i - x_j}$

设 $F(x) = \prod_j (x - x_j) = \prod_j (x - \omega^j)$ ，考虑代数基本定理，那么知道 $F(x) = x^n - 1$ 。

现在我们需要 $\frac {x^n - 1}{x - \omega^j}$ ，考虑除法模拟展开：

f_{j} (x) = \frac{F (x)}{x - ω_{j}} = x^{n - 1} + ω^{j} x^{n - 2} + ω^{2 j} x^{n - 3} + \dots + ω^{(n - 1) j} x^{0}

$f_j(x) = \frac {F(x)} {x - \omega_j} = x^{n - 1} + \omega^j x^{n - 2} + \omega^{2j} x^{n - 3} + \cdots + \omega^{(n - 1)j} x^0$

于是

(V^{- 1})_{i, j} = \frac{[x^{i}] f_{i} (x)}{f_{i} (ω^{j})} = \frac{ω^{j (n - 1 - i)}}{n ω^{j (n - 1)}} = \frac{ω^{- i j}}{n}

$(V^{-1})_{i, j} = \cfrac {[x^i] f_i(x)}{f_i(\omega^j)} = \frac {\omega^{j(n - 1 - i)}}{n \omega^{j(n - 1)}} = \cfrac {\omega^{-ij}}{n}$

也就得到了其逆矩阵：

\frac{1}{n} [\begin{matrix} 1 & 1 & 1 & 1 & \dots & 1 \\ 1 & ω_{n}^{- 1} & ω_{n}^{- 2} & w_{n}^{- 3} & \dots & ω_{n}^{- (n - 1)} \\ 1 & ω_{n}^{- 2} & ω_{n}^{- 2 \times 2} & ω_{n}^{- 2 \times 3} & \dots & ω_{n}^{- 2 \times (n - 1)} \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋱ & \dots \\ 1 & ω_{n}^{- (n - 1) \times 2} & ω_{n}^{- (n - 1) \times 3} & ω_{n}^{- (n - 1) \times 2} & \dots & ω_{n}^{- (n - 1) \times (n - 1)} \end{matrix}]

$\frac 1 n \begin{bmatrix} 1 & 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n^{-1} & \omega_n^{-2} & w_n^{-3} & \cdots & \omega_n^{-(n-1)} \\ 1 & \omega_n^{-2} & \omega_n^{-2\times2} & \omega_n^{-2\times3} & \cdots & \omega_n^{-2\times(n-1)}\\ \vdots & \vdots & \vdots & \vdots & \ddots & \cdots \\ 1 & \omega_n^{-(n-1)\times2} & \omega_n^{-(n-1)\times3} & \omega_n^{-(n-1)\times2} & \cdots & \omega_n^{-(n-1)\times(n-1)} \end{bmatrix}$

这就是 IDFT 的本质。

于是，我们可以得出两个多项式卷积的计算方法：

将两个多项式改写为向量的形式，并分别对其做一次离散傅里叶变换 (DFT)
将变换过后的两个序列相乘（点对点相乘）得出一个新的序列
我们再对此序列做一次逆傅里叶变换，也就是将序列变为 $\langle g(\omega^{-0}), g(\omega^{-1}),g(\omega^{-2}), \dots, g(\omega^{-(n-1)}) \rangle$

也就是 $\langle n \times c_0, n \times c_1, \dots, n \times c_{n-1} \rangle$

最后对于每一项除以 $n$ 即可。

但是：

最朴素的 DFT 变化的时间复杂度为 $O(n^2)$ ，三次变换还不如直接暴力计算……所以我们就需要快速傅里叶变换来优化了。

快速傅里叶变换（FFT）

FFT $\to$ Fast-Fast-TLE

我们对于 $f(x) = c_0 + c_1 x + c_2 x^2 + \dots + c_{n-1}x^{n-1}$ ，分离其奇数项和偶数项，构造出另外两个向量

\begin{aligned} f_{e v e n} (x) & = c_{0} + c_{2} x + c_{4} x^{2} + \dots + c_{n - 2} x^{\frac{n}{2} - 1} \\ f_{o d d} (x) & = c_{1} + c_{3} x + c_{5} x^{2} + \dots + c_{n - 1} x^{\frac{n}{2} - 1} \end{aligned}

$\ \begin{aligned} f_{even}(x) &= c_0 + c_2 x + c_4 x^2 + \dots + c_{n-2} x^{\frac n2 - 1} \\ f_{odd}(x) &= c_1 + c_3 x + c_5 x^2 + \dots + c_{n-1} x^{\frac n2 - 1} \\ \end{aligned}$

那么，不难发现：

f (x) = f_{e v e n} (x^{2}) + x f_{o d d} (x^{2})

$f(x) = f_{even}(x^2) + x f_{odd}(x^2)$

也就是说

\begin{aligned} f (ω_{n}^{k}) & = f_{e v e n} (ω_{n}^{2 k}) + ω_{n}^{k} f_{o d d} (ω_{n}^{2 k}) \\ f (ω_{n}^{k + \frac{n}{2}}) & = f_{e v e n} (ω_{n}^{2 k + n}) + ω_{n}^{k + \frac{n}{2}} f_{o d d} (ω_{n}^{2 k + n}) \end{aligned}

$\begin{aligned} f(\omega_n^k) &= f_{even}(\omega_{n}^{2k}) + \omega_n^kf_{odd}(\omega_n^{2k}) \\ f(\omega_n^{k+\frac n2}) &= f_{even}(\omega_n^{2k+n}) + \omega_n^{k+\frac n2}f_{odd}(\omega_n^{2k+n}) \end{aligned}$

补充一个点：

$\omega_n^{\frac n2} = -1$
证明：考虑我们在上面画出的图中， $\omega_n^{\frac n2}$ 所在的位置。就是 -1 了

再根据单位根的消去原理稍微化一下……

\begin{aligned} f (ω_{n}^{k}) & = f_{e v e n} (ω_{\frac{n}{2}}^{k}) + ω_{n}^{k} f_{o d d} (ω_{\frac{n}{2}}^{k}) \\ f (ω_{n}^{k + \frac{n}{2}}) & = f_{e v e n} (ω_{\frac{n}{2}}^{k}) - ω_{n}^{k} f_{o d d} (ω_{\frac{n}{2}}^{k}) \end{aligned}

$\begin{aligned} f(\omega_n^k) &= f_{even}(\omega_{\frac n2}^k) + \omega_n^kf_{odd}(\omega_{\frac n2}^k) \\ f(\omega_n^{k+\frac n2}) &= f_{even}(\omega_{\frac n2}^k) - \omega_n^kf_{odd}(\omega_{\frac n2}^k) \\ \end{aligned}$

于是，我们就可以递归分治了。

其时间为 $T(n) = 2T(n/2) + O(n)$

故复杂度为 $T(n) = O(nlogn)$ 。

其实我们还要考虑一点，我们要保证长度为 $2^k$ 才能保证可以正确的分治

因为只有长度相等的区间才能合并（考虑此时单位根才一样）。

所以说，我们要把两个多项式通过补 $0$ 的方式补齐到 $2^k$ 项，合并之后就是 $2^{k+1}$ 项。

对于模板题：【模板】多项式乘法（FFT） - 洛谷

可以写出如下龟速代码：

#include <iostream>
#include <algorithm>
#include <vector>

struct Complex {
    double real, imag;
    Complex() : real(0), imag(0) {}
    Complex(double re, double im) : real(re), imag(im) {};
    inline Complex operator + (const Complex & b) { return Complex(real + b.real, imag + b.imag); }
    inline Complex operator - (const Complex & b) { return Complex(real - b.real, imag - b.imag); }
    inline Complex operator * (const Complex & b) { return Complex(real * b.real - imag * b.imag, real * b.imag + imag * b.real); }
};
typedef std::vector<Complex> Vector;

const double PI = acos(-1);

void FFT(Vector &v, int n, int inv) {
    if (n == 1) return; // 递归边界，只有一个元素，不做变换

    // 奇偶变化为两个向量
    int mid = n >> 1;
    Vector even(mid), odd(mid);
    for (int i(0); i < n; i += 2) {
        even[i >> 1] = v[i], odd[i >> 1] = v[i + 1]; 
    }
    // 递归操作 
    FFT(even, mid, inv), FFT(odd, mid, inv);

    // 进行合并操作
    // 定义基本 omega
    Complex omega(cos(PI * 2 / n), inv * sin(PI * 2 / n));
    // 当前旋转因子
    Complex w(1, 0);
    for (int i(0); i < mid; ++i, w = w * omega) {
        v[i] = even[i] + w * odd[i];
        v[i + mid] = even[i] - w * odd[i];
    }
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0), std::cout.tie(0);

    int n, m;
    std::cin >> n >> m;

    // 获取最终的长度，必须是 2 的次幂，且比两个向量卷起来要长 
    int O(1);
    while (O <= m + n) O <<= 1;
    // std::cout << PI << " " << O << std::endl;

    Vector A(O), B(O);
    for (int i(0); i <= n; ++i) std::cin >> A[i].real; 
    for (int i(0); i <= m; ++i) std::cin >> B[i].real;

    FFT(A, O, 1);
    FFT(B, O, 1);

    // 我们单点相乘，然后进行逆变换，求出每一项的系数
    for (int i(0); i < O; ++i) A[i] = A[i] * B[i];
    FFT(A, O, -1);

    // 最后进行输出
    // 记得两个东西卷起来之后是 n + m 次的
    for (int i(0); i <= n + m; ++i) {
        // 这里是向上取整？ 
        std::cout << (long long)(A[i].real / O + 0.5) << ' ';
    } std::cout << std::flush;
    return 0;
}

我不知道为什么网上这么多写递归版本的都是错的。

例如本题第一篇题解，其实并不是方法有问题，是他的写法错了。

链接：题解 P3803 【【模板】多项式乘法（FFT）】 - attack 的博客

例如知乎上的一篇文章，其在递归时的边界是有问题的。虽然说不影响正确性……

链接：快速傅里叶变换 - 星夜

当然，还是有代码正确，但是代码……

链接：FFT-快速傅里叶变换 - heartbeats

有一个不算优化的优化。考虑每一层所需要的空间是固定的。所以考虑预先分配 $O(n \log n)$ 的空间，然后直接使用即可。

蝶形优化

在运行FFT的递归版本时，可以观察到递归树如下：

如果我们把初始向量 $a$ 中的元素按照其在叶子中出现的次序进行安排，就可以对递归过程进行追踪，不过是自底向上，而非自顶向下。

回顾 FFT 合并时的代码：

for (int i(0); i < mid; ++i, w = w * omega) {
    v[i] = even[i] + w * odd[i];
    v[i + mid] = even[i] - w * odd[i];
}

在这个循环中，我们只用到了两个值：even[i], odd[i]，得到了两个值：v[i], v[i + mid]。我们利用一种图示表示：

我们称这个操作为蝴蝶操作。

那么整个计算FFT的过程可以通过此图表示：

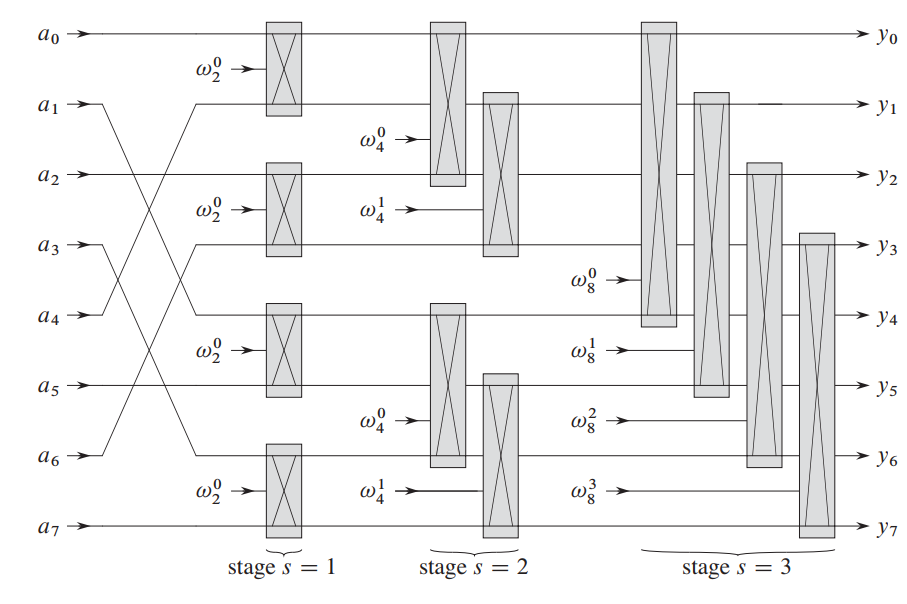
这个地方确实比较绕，难以通过语言表述，不过通过上面 $4$ 张图，请读者停下稍微悟一悟。

其实从第一个递归的图中，我们已经可以发现初始值的规律了：

我们通过观察其二进制得出答案：下标的二进制恰好和目标二进制互为倒序。

一共只有 $\log(n)$ 位！也就是保证所有数拥有一样多的比特位。

也就是说当 $n = 8$ 时 rev[3] = rev[0b011] = 0b110 = 6, $\log8 = 4$

我们考虑可以通过 DP 在 $O(n)$ 内实现。

假设我们已经处理完了 $1 \sim n-1$ 的所有 $rev$ 。

考虑 $n = (abcd)_2$ ，此时我们已经知道了 $rev[(0abc)_2] = (cba0)_2$ ，需要 $rev[(abcd)_2] = (dcba)_2$

通过瞪眼法，我们可以轻易的得出

$rev[(abcd)_2] = (dcba)_2 = (rev[(0abc)_2]>>1)\ | \ ((d\&1)<<3)$

改写为递推式即是：

dp[x] = (dp[x>>1] >> 1) | ((x&1) << (log2(n) - 1))

参考代码：

#include <complex>
#include <iostream>
#include <algorithm>
#include <vector>

struct Complex {
    double real, imag;
    Complex() : real(0), imag(0) {}
    Complex(double re, double im) : real(re), imag(im) {};
    inline Complex operator + (const Complex & b) { return Complex(real + b.real, imag + b.imag); }
    inline Complex operator - (const Complex & b) { return Complex(real - b.real, imag - b.imag); }
    inline Complex operator * (const Complex & b) { return Complex(real * b.real - imag * b.imag, real * b.imag + imag * b.real); }
};

typedef std::vector<Complex> Vector;

const double PI = acos(-1);
int O(1), logO(0);

void FFT(std::vector<int> &rev, Vector &v, int inv) {
    for (int i(0); i < O; ++i) {
        if (i < rev[i]) std::swap(v[i], v[rev[i]]);
    }

    // 第 log(k) 次合并，一共logO次 
    // 合并之后区间的长度为 k
    for (int k(1); k < O; k <<= 1) {
        Complex omega(cos(PI / k), inv * sin(PI / k));
        for (int i(0); i < O; i += (k<<1)) { // 处理行 
            Complex w(1, 0);
            for (int j = 0; j < k; ++j, w = w * omega) {
                Complex s = v[i + j], t = v[i + j + k] * w;
                v[i + j] = s + t, v[i + j + k] = s - t; 
            }
        }
    }

    if (inv == -1) for (int i(0); i < O; ++i) v[i].real /= O;
}


int main() {
    int n, m;
    std::cin >> n >> m;

    while (O <= n + m) O <<= 1, ++logO;

    Vector A(O), B(O);
    for (int i(0); i <= n; ++i) std::cin >> A[i].real; 
    for (int i(0); i <= m; ++i) std::cin >> B[i].real;

    std::vector<int> rev(O);
    for (int i(0); i < O; ++i) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (logO - 1));

    FFT(rev, A, 1), FFT(rev, B, 1);

    for (int i(0); i < O; ++i) A[i] = A[i] * B[i];
    FFT(rev, A, -1);

    for (int i(0); i <= n + m; ++i) {
        std::cout << (long long)(A[i].real + 0.1) << ' '; // 向上取整 
    } std::cout << std::flush;
    return 0;
}

那么恭喜你，大概是明白了 FFT 了吧！

快速数论变换（NTT）

快速数论变换我们可以类比快速傅里叶变换。只是将复数优化为了取模实数。

在模 $p$ 意义下，会存在 $a^{(p-1)} \equiv 1 \pmod p$ 。

于是我们找到 $\Z_p$ 中的一个原根 $g$ 。

可以参考：算法学习笔记(11): 原根 - jeefy - 博客园

满足：

$\begin{aligned} \forall x \in [1, \varphi(p)), g^x \not\equiv 1 \pmod p \\ g^{\varphi(p)} \equiv 1 \pmod p \end{aligned}$
的数 $g$ 即是 $\Z_p$ 中的一个原根。

那么如何构造一个满足单位根性质的数？

令 $v = \varphi(p)$ ，考虑：

w_{n} = g^{\frac{v}{n}}

$w_n = g^{\frac vn}$

显然，有 $g_n \equiv 1 \pmod p$

后文中为了方便，就不写后面的 $\pmod p$ 了。

如果

n

$n$ 不能整除

v

$v$ 怎么办？凉拌

这也就是我们为什么把模数设为 $998244353 = 119*2^{23} + 1$ 或者 $167772161 = 5*2^{25}+1$

那么我们来证明其满足作为单位根需要的三个性质：

消去： $w_{dn}^{dk} = w_n^k$

证明：考虑展开即可： $w_{dn}^{dk} = g^{\frac v{dn} dk} = g^{\frac nk}$
折半： $(w_n^{k+\frac n2})^2 = w_n^{2k + n} = w_n^{2k} = w_{\frac n2}^k$
求和： $\sum_{i=0}^{n-1} (\omega_n^k)^i = 0$

证明：也考虑等比数列：

$\begin{aligned} \sum_{i=0}^{n-1} (\omega_n^k)^i &= \cfrac {(w_n^k)^n - 1}{w_n^k - 1} \\ &= \cfrac {(w_n^n)^k - 1}{w_n^k - 1} \\ &= \cfrac {1^k - 1}{w_n^k - 1} = 0 \end{aligned}$
这过程怎么一模一样……

那么我们可以将单位根替换，进行变换了！

说实话，代码几乎是一模一样的……

const int MOD = 998244353, g = 3, ig = 332748118;
int O(1), logO(0);

typedef vector<long long> vec;
typedef vector<int> ivec;

void NTT(ivec &rev, vec &v, int inv) {
    for (int i(0); i < O; ++i) {
        if (rev[i] < i) std::swap(v[i], v[rev[i]]);
    }

    // 第 log(k) 次合并
    for (int k(1); k < O; k <<= 1) {
        long long omega = qpow((long long)(~inv ? g : ig), (MOD - 1) / (k << 1), MOD);
        for (int i(0); i < O; i += (k << 1)) {
            long long w(1);
            for (int j(0); j < k; ++j, w = w * omega % MOD) {
                long long s = v[i + j], t = w * v[i + j + k];
                v[i + j] = (s + t) % MOD, v[i + j + k] = ((s - t) % MOD + MOD) % MOD;
            }
        }
    }

    if (inv == -1) {
        for (int iv(qpow((long long)O, MOD - 2, MOD)), i(0); i < O; ++i) {
            v[i] = v[i] * iv % MOD;
        }
    }
}

而且由于没有了复数，常数会小很多（比FFT快）

FFT 的其他

循环卷积：这里卷积的结果实际上是 $c_k = \sum_{i + j \equiv k \pmod n} a_i b_j$ 。
任意模数 NTT：模 $p$ 意义下结果值域大概是 $O(n^2 p)$ 级别的，所以需要三个 $\prod > n^2 p$ 的模数以及 CRT 完成。
拆系数FFT：也就是把值放在 $\sqrt M$ 进制下运算，那么值域就减到 $O(n p)$ 级别了，非常优秀。

posted @ 2023-02-10 15:28 jeefy 阅读(850) 评论(1) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 算法学习笔记(38): 矩阵

· 算法学习笔记(45): 快速沃尔什变换 FWT

· 关于FFT

· [笔记]快速傅里叶变换（FFT）

· 快速傅里叶/数论变换学习简记

阅读排行：
· DeepSeek 开源周回顾「GitHub 热点速览」
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· .NET 10首个预览版发布：重大改进与新特性概览！
· AI与.NET技术实操系列（二）：开始使用ML.NET
· 单线程的Redis速度为什么快？

公告

昵称： jeefy
园龄： 2年1个月
粉丝： 32
关注： 13

+加关注

2025年3月

日

一

二

三

四

五

六

jeefy

信仰，梦想，希望！

算法学习笔记(17): 快速傅里叶变换（FFT）

快速傅里叶变换（FFT）

虚数

重要性质

代码实现

单位根

三个引理

多项式

离散傅里叶变换(DFT)

离散傅里叶逆变换（IDFT）

快速傅里叶变换（FFT）

蝶形优化

快速数论变换（NTT）

FFT 的其他

公告

最新随笔

我的标签

合集 (7)

随笔分类 (105)

阅读排行榜

推荐排行榜