学习 JavaScript 树
学习 JavaScript 树
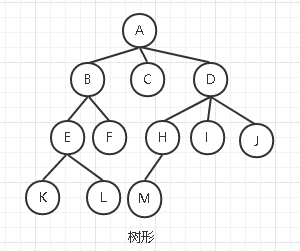
树(Tree)
在计算机科学中,数据结构是一门研究非数值计算的程序设计问题中计算机的操作对象(数据元素)以及它们之间的操作和运算等的学科。
它包含三方面的内容:
- 数据的逻辑结构(常见有树、图、集合、线性)
- 数据存储结构(线性结构和链表结构)
- 数据的操作(删除、查询、添加等非数值计算的问题)
而树是其中一种逻辑结构,除了我们上图👆↑的树模型外,还有以下的其他表示方法(图片来源网络,侵删)
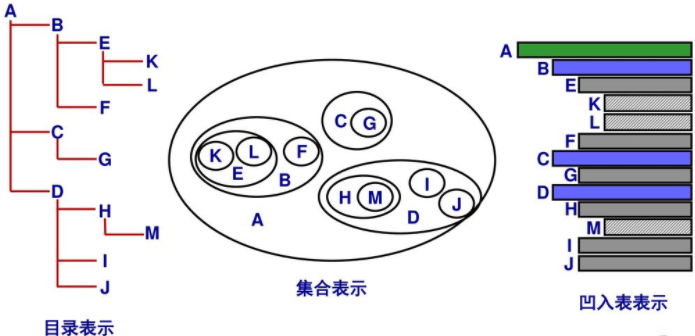
可见,树形结构能表示一种具有层次的分支关系,节点之间的关系构成了层次,每个节点最多有一个前驱(父亲),但可有多个后继(孩子)。有且只有一个根节点,其余节点又分为多个不相交的有限集合,而每个集合又是一棵树。显然树满足递归定义,在后面介绍二叉树的遍历中将有应用cursion递归。
而这个“目录表示”跟我们常说的HTML中DOM树形结构是一样的,因此我们可以把DOM元素存入逻辑树中(二叉树、多叉树),可以很方便地实现DOM元素的修改、移除、添加、查询等操作。关于树的种类、树的基本术语见维基百科]树 (数据结构)
以上展示的均为多叉树,下面介绍最为简单、最有规律的二叉树,然后设法把一般的树转化为简单树来实现树的操作。
二叉树(Binary Tree)
二叉树的概念
二叉树是节点的有限集合,这个集合或者为空集,或者由一个根节点及两棵不相交的、分别称为这个根的左子树和右子树的二叉树组成。
基本特征:
- 每个结点最多只有两棵子树(不存在度大于2的结点);
- 左子树与右子树顺序不能颠倒;
- 每一个节点都是一个对象,每个数据结点都有三个指针,分别指向父母、左孩子和右孩子的指针。
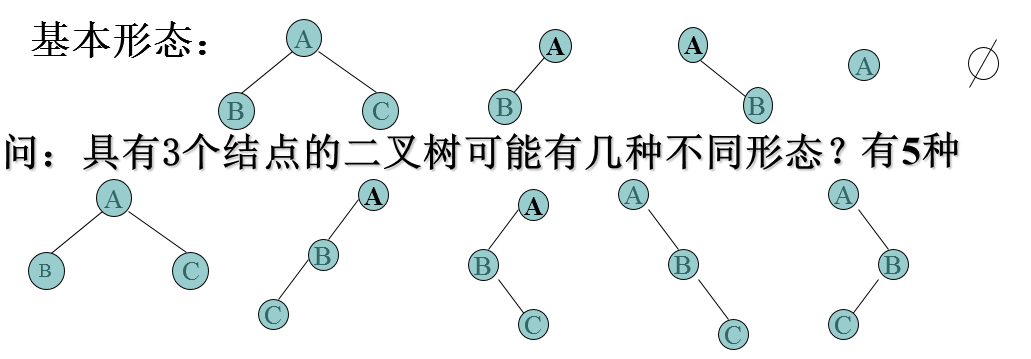
二叉树的存储结构
有了二叉树的逻辑结构后,在对树操作之前,需要把它存入计算机中,主要有顺序(线性)存储结构和链式存储结构。
顺序存储结构:采用从上到下,从左到右的顺序把树的结点从 0 到 n-1 存放到一维数组中,通过数组元素的下标关系来确定二叉树中的逻辑关系。
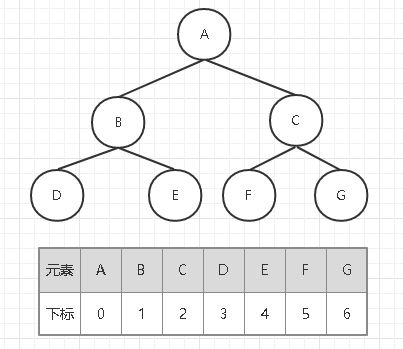
上图为完全二叉树的顺序存储结构,若是一般的非完全二叉树则要额外增添一些不存在的空节点,使之变成完全二叉树才能继续通过下标反映结点之间的逻辑关系。如果使用链式存储结构,则不会有这个问题。
链式存储结构:每个结点包含三个域,数据域data、左孩子指针域lchild和右孩子指针域rchild。

使用链式存储结构实现二叉树节点的定义
function node(data) {
this.data = data;
this.left = null
this.right = null;
}
对于DOM元素结构这样的多叉树来说,则可以转变为以下的定义
function node(data) {
this.data = data;
parent = null;
children = [];
}
树的遍历(Tree Traversal)
从树的根结点出发,按照某种顺序来访问每个节点,使每个节点被访问有且仅有一次。树的遍历是树结构插入、删除、修改、查找和排序的前提,对每个节点访问通常是“先左后右”。
遍历的种类
1. 深度优先遍历(对于二叉树又可以分为以下三种)
1. DLR——先(根)序遍历
2. LDR——中(根)序遍历
3. LRD——后(根)序遍历
2. 广度优先遍历(按层次从上到下,从左到右依次访问)
由于从给定的节点出发,有多个可以前往的下一个结点(与线性的数据结构如一维数组不同),因此需要以某种方式存储起来稍后再访问,常见的做法是采用栈和队列,在javascript中可以通过数组的方法pop()、push()和shift()来模拟栈和队列。
深度优先遍历(Depth Firsh Search)
深度优先遍历,先访问父节点,然后访问第一个子结点,第二个子节点等,那么如何保证访问的顺序呢?通过堆栈的特点,先把第二个子节点压栈,再把第一个子节点压栈,最后把父节点放在栈顶,根据栈的后入先出特定,则可以保证遍历的时候根节点在栈顶,最先被访问到,其次才到子节点。
stack(后入先出)
var stack = [];
// 入栈
stack.push(5); // stack is now [5]
stack.push(2); // stack is now [5, 2]
stack.push(0); // stack is now [5, 2, 0]
// 出栈
var i = stack.pop(); // stack is now [5, 2]
alert(i); // display 0
先(根)序遍历
递归算法:若二叉树为空,则空操作;否则,进行以下操作
- 访问根结点
- 先序遍历访问根节点的左子树
- 先序遍历访问根节点的右子树
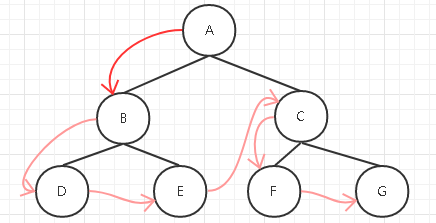
先序遍历顺序:A B D E C F G
function preOrderTraverse(node) {
if (!node == null) {
callback(node); // 输出当前节点
preOrderTraverse(node.left);
preOrderTraverse(node.right);
}
}
// 回调函数
var callback = function(key) {
console.log(key);
};
中(根)序遍历
递归算法:若二叉树为空,则空操作;否则进行以下步骤
- 中序遍历访问根节点的左子树
- 中序遍历访问根节点
- 中序遍历访问根节点的右子树
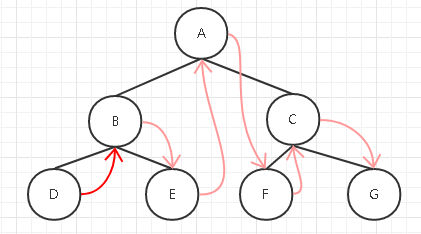
中序遍历顺序:D B E A F C G
function inOrderTraverse(node) {
if (!node == null) {
preOrderTraverse(node.left);
callback(node); // 输出当前节点
preOrderTraverse(node.right);
}
}
后(根)序遍历
递归算法:若二叉树为空,则空操作;否则进行以下步骤
- 后序遍历访问根节点的左子树
- 后序遍历访问根节点的右子树
- 后序遍历访问根节点
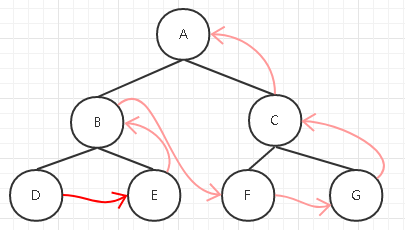
后序遍历顺序:D B E A F C G
function postOrderTraverse(node) {
if (!node == null) {
preOrderTraverse(node.left);
preOrderTraverse(node.right);
callback(node); // 输出当前节点
}
}
广度优先遍历(Breadth First Search)
又叫横向遍历,从上下到下,从左到右,一层层往下访问节点。要实现这个顺序,则要考虑队列的存储特点“先入显出”,先将左子树入列,再将右子树入列,这样在出列的时候左子树先出再到右子树。
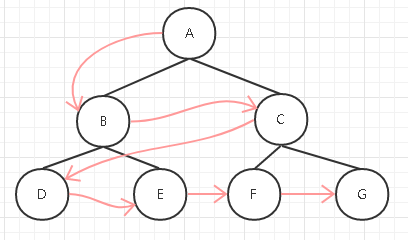
广度优先遍历顺序:A B C D E F G
queue(先入先出)
var queue = [];
// 入列
queue.push(5); // queue is now [5]
queue.push(2); // queue is now [5, 2]
queue.push(0); // queue is now [5, 2, 0]
// 出列
var i = queue.shift(); // queue is now [2, 0]
alert(i); // dispaly 5
二叉查找树(Binary Search Tree)
二叉查找树(或者说二叉排序树):左节点小于根节点,右节点大与根节点。
二叉查找比普通查找、删除更快的原因在于,可以根据要查找、删除的节点与当前节点的比较以及二叉排序树本身的特点(左子节点总是比根节点小,右子节点比根节点大),不用遍历全部节点就可以快速找到指定节点。(下图查找节点7)

查找最小值:根据二叉排序树的特点,只需遍历左子树,直到找到最后一个节点(它的孩子节点current.left = null)
function getMinNode(node) {
if(node) {
while(node && node.left !== null) {
node = node.left;
}
return node.data;
}
}
查找最大值:只需遍历右子树,直到找到最后一个节点(它的孩子节点current.right = null)
function getMaxNode(node) {
if(node) {
while(node && node.right !== null) {
node = node.right;
}
return node.data;
}
}
删除节点有两种情况,一种是删除叶子节点(没有孩子节点,直接删除),另一种是删除普通节点(要考虑只有左子树和只有右子树、同时都有左右子树),删除普通节点在不删除该节点的子节点下,要把它的子节点与它的父节点重新链接,从而保证删除后的二叉树仍然满足左节点小于根节点,右节点大于根节点,保持排序顺序。
普通节点:
- 只有左子树或右子树

- 有左、右字树

实现原理:把当前节点下的右子树的最小节点找出来,把最小节点赋予给当前节点,然后把该最小节点删除。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号