递归函数与二分查找算法

目录

• 楔子
• 二分查找算法

 

---

回到顶部

楔子

如果有这样一个列表，让你从这个列表中找到66的位置，你要怎么做？

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

你说，so easy！

l.index(66)...

我们之所以用index方法可以找到，是因为python帮我们实现了查找方法。如果，index方法不给你用了。。。你还能找到这个66么？

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

i = 0
for num in l:
    if num == 66:
        print(i)
    i+=1

上面这个方法就实现了从一个列表中找到66所在的位置了。

但我们现在是怎么找到这个数的呀？是不是循环这个列表，一个一个的找的呀？假如我们这个列表特别长，里面好好几十万个数，那我们找一个数如果运气不好的话是不是要对比十几万次？这样效率太低了，我们得想一个新办法。

回到顶部

二分查找算法

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

你观察这个列表，这是不是一个从小到大排序的 有序 列表呀？

如果这样，假如我要找的数比列表中间的数还大，是不是我直接在列表的后半边找就行了？

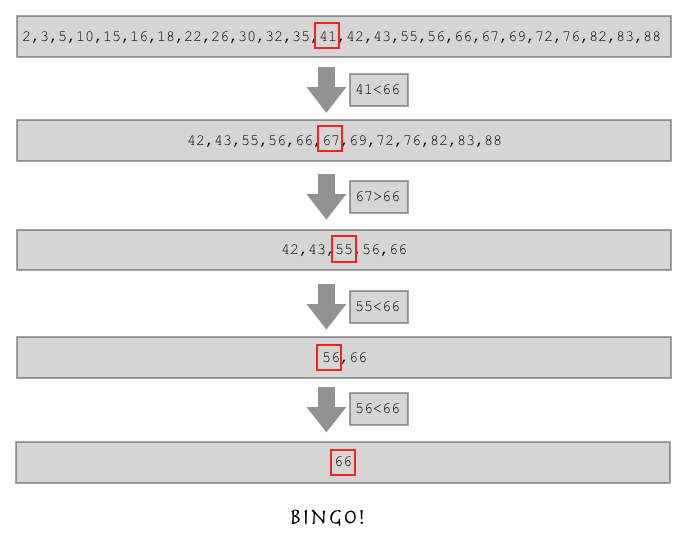
这就是 二分查找算法 ！

那么落实到代码上我们应该怎么实现呢？

简单版二分法

def find(l, num):
    if l:
        mid = (len(l)-1)//2
        if l[mid] > num:
            # 从左边找
            find(l[:mid], num)
        elif l[mid] < num:
            # 从右边找
            find(l[mid+1:], num)
        else:
            print('找到啦')
    else:
        print('找不到')

升级版二分法

def find2(l, num, start=0, end=None):
    end = end if end else len(l) - 1
    mid = (end-start)//2 + start
    if start >= end:
        print('找不到')
    elif l[mid] > num:
        find2(l, num, end=mid)
    elif l[mid] < num:
        find2(l, num, start=mid+1, end=end)
    else:
        print('找到啦', mid)