图的基本概念（一）

一、什么是图？

一个图可以形式定义为一个二元组：  G = ( V, E )，其中：

（1）V 是顶点（结点）的有穷集合。

（2）E是连接V中两个不同顶点（顶点对）的边的有限集合。 如果E中的顶点对是有序的，即E中的每条边都是有方向的，则称G为有向图。如果顶点对是无序对，则称G是无向图。

 

二、有向图和无向图

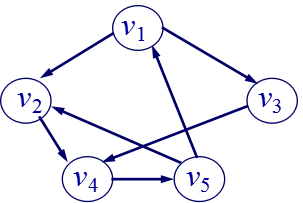
下面左边的图是一个有向图，可以描述为：G = (V, E)，其中V = {v1,v2,v3,v4,v5}E = {<v1, v2>,<v1, v3>,<v2, v4>,<v3, v4>,<v4,v5>,<v5, v2>, <v5, v1>}

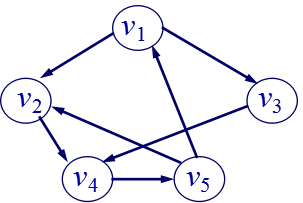
下面右边的图是一个无向图，可描述为：G = (V, E)，其中V = {v1,v2,v3,v4,v5, v6}E = {(v1, v2),(v1, v6),(v2, v5),(v2, v6),(v3,v5),(v3, v4),(v4, v5)}

                                                                

 

三、基本概念

1.对于无向图而言，假若顶点v和顶点w 之间存在一条边(v,w) ，则称v 和w是相邻的，顶点v 和w 互为邻接顶点。边(v,w) 和顶点v 和w 相关联。（对于有向图，称为邻接到和邻接自。）

2.对于无向图而言，从顶点v到顶点w的路径指的是一个顶点序列(v = v0v1…vm= w)，其中(vi,vi+1)∈E。路径的长度指的是路径上的边的数目。（对于有向图，也可以定义路径，且路径是有向的。）

3.若路径中的顶点没有重复，称为简单路径。

4.第一个顶点和最后一个顶点相同的路径称为环或回路。

5.在无向图中，如果从顶点v到顶点w有路径，则称顶点v和顶点w是连通的。

6.如果无向图G中任意两个顶点都是连通的，则称图G是连通图。

8.如果一个无向图不是连通图，则其中的每个极大连通子图称为无向图的连通分量。

9.如果有向图G中任意两个顶点间都存在有向路径（对任意两个顶点v和w，既存在v到w的有向路径，也存在w到v的有向路径），则称有向图G是强连通图。

10.其各个极大强连通子图称作它的强连通分量。 如果不考虑有向图中边的方向所得到的无向图是连通图，则有向图称为弱连通图。

11.对于无向图而言，和顶点相关联的边的数目称为顶点的度。

12。对于有向图而言，从顶点出发的边的数目称为顶点的出度，到达该顶点的数目称为顶点的入度。 边上带有权值的有向图或无向图分别称作有向网或无向网。

图的基本概念可以参考：《大话数据结构》p213 - p222 

 

 

关于红黑树，以后用到再具体的学习，现在只是大致的了解下：

补充记录下红黑树的基本性质：

红黑树的特性:
（1）每个节点或者是黑色，或者是红色。
（2）根节点是黑色。
（3）每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]
（4）如果一个节点是红色的，则它的子节点必须是黑色的。
（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

红黑树的相关资料参考：https://www.cnblogs.com/skywang12345/p/3245399.html