高等数学笔记
高等数学概念、公式及常用结论
内容整理来源于网络,可能存在疏漏和错误,若有侵权请 联系作者 jeanhua_official@outlook.com 删除
第一章 函数 极限 连续
常用的基本极限
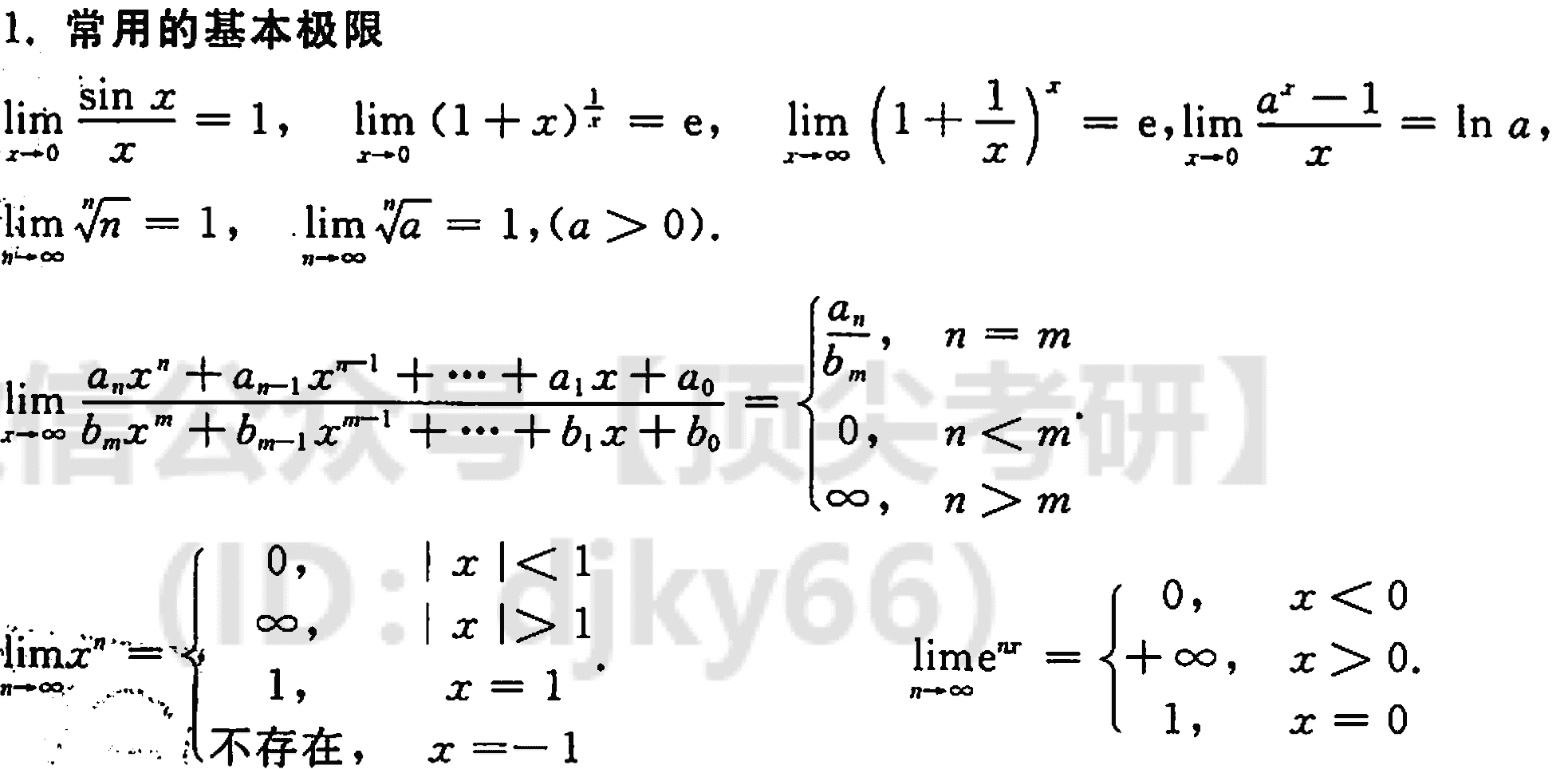
1-无穷型 极限常用结论
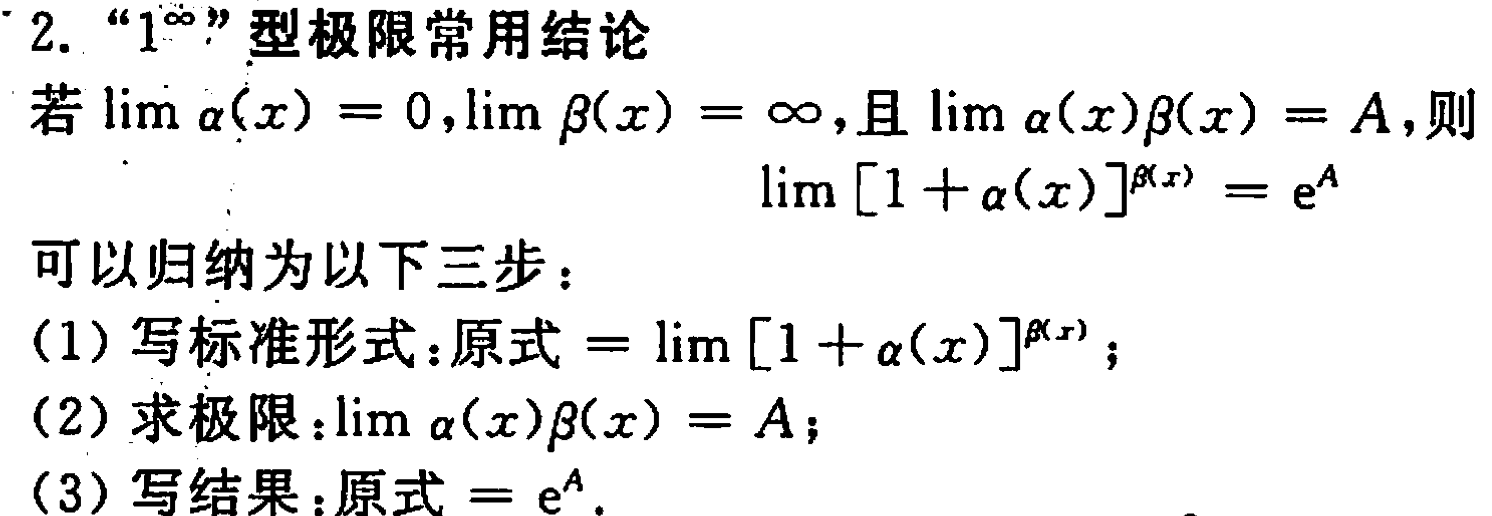
常用的等价无穷小



x→∞,有时也可以使用等价无穷小代换。只要函数内部是无穷小即可。比如,x→∞时,sin(1/x)~1/x。

洛必达法则求极限
什么时候可以用洛必达法则

洛必达法则的适应类型
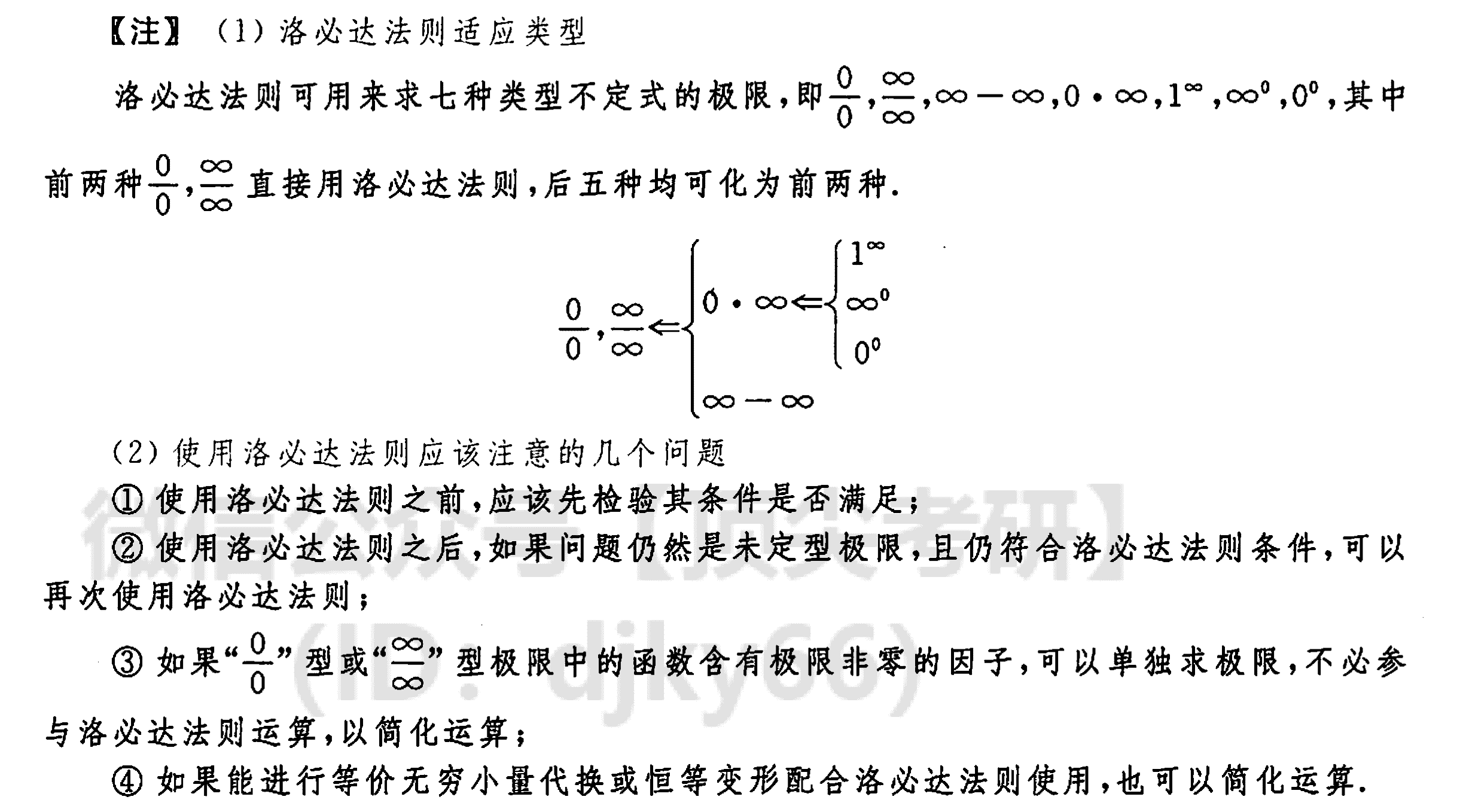
泰勒公式求极限
略,见下一章
利用单调有界准则求极限
- 证明极限存在(单调有界)
- 等式两端取极限进行运算
求极限时的常用结论
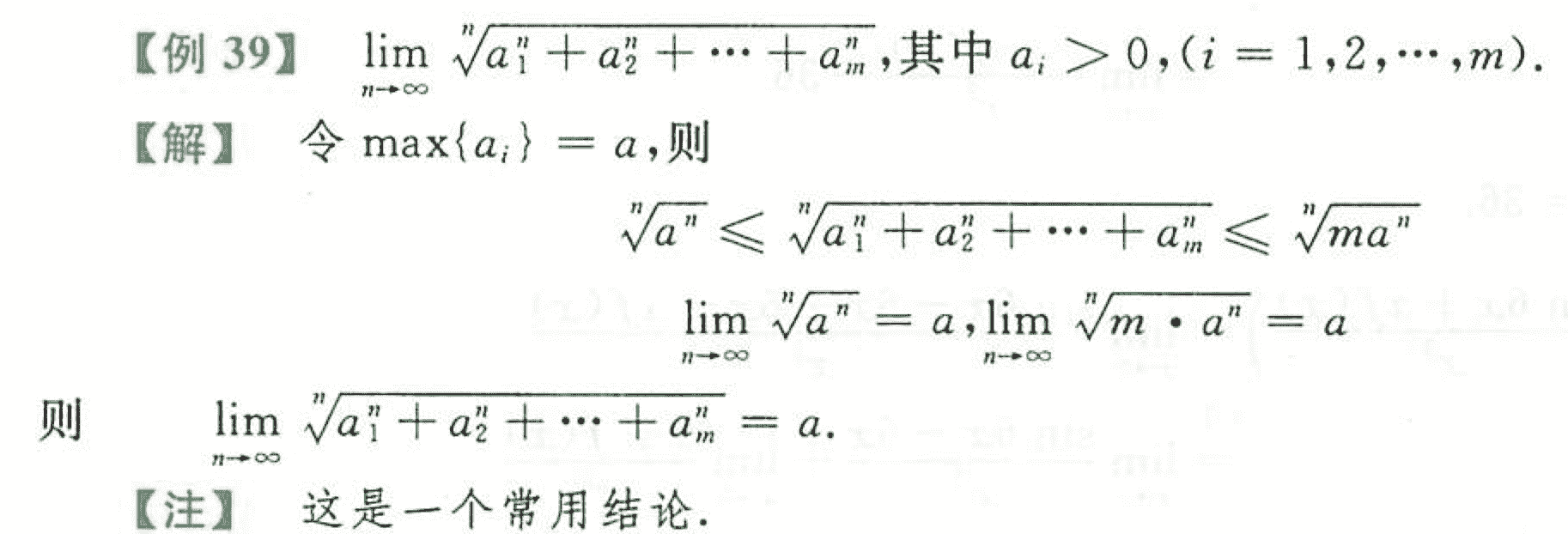
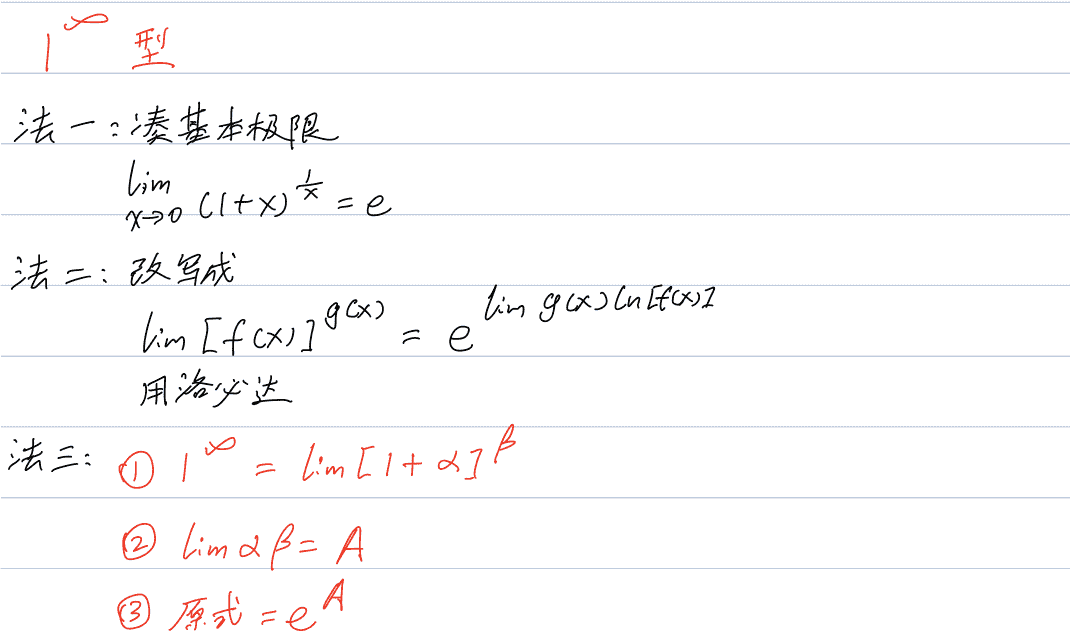
1.先证明有界性
在利用单调有界准则求极限的时候,几个常用不等式一定要想到下列不等式来证明有界性!!!
-
两个正数乘积或者两个正数相加的时候:
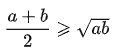
-
三个(或以上)正数相乘相加:
算数平均值、几何平均值
2.再证明单调性
- 后项减前项
- 后项比前项
无穷小量阶的比较(其实就是0比0极限计算)
- 洛必达法则
- 等价代换
- 泰勒展开式
第二章 导数与微分
导数与微分的概念
导数与微分的几何意义
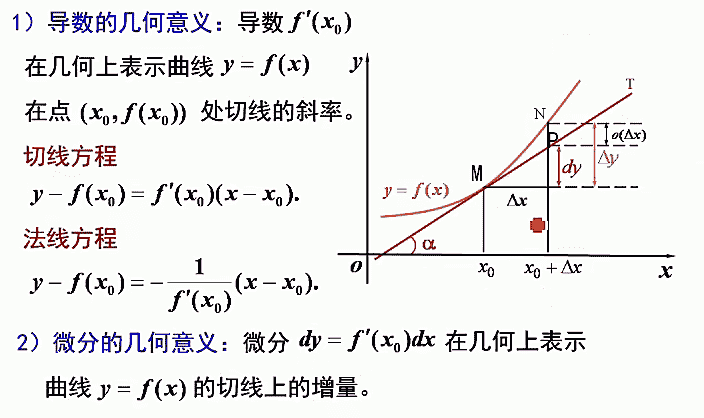
微分dy是切线上的改变量。用dy来代替$\Delta$y,几何上是用切线上的改变量来代替实际上曲线上的改变量。换言之,再微小的局部,用直线的均匀变化来代替曲线的非均匀变化。
导数定义证明常用方法
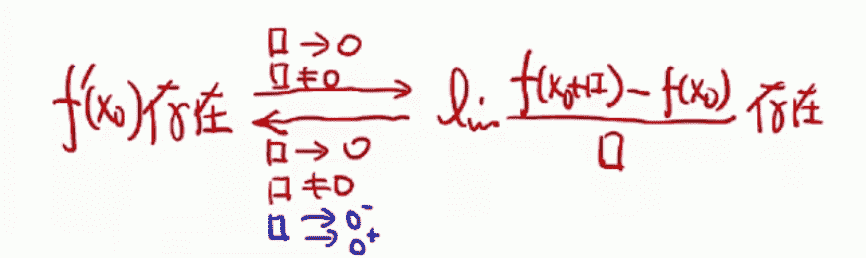
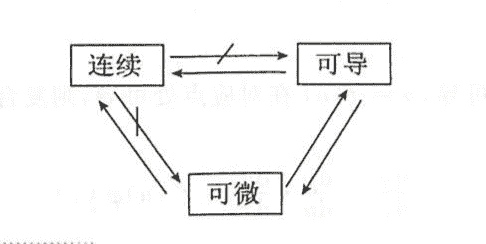
连续、可导、可微之间的关系
倒数公式及求导法则
基本初等函数的导数公式
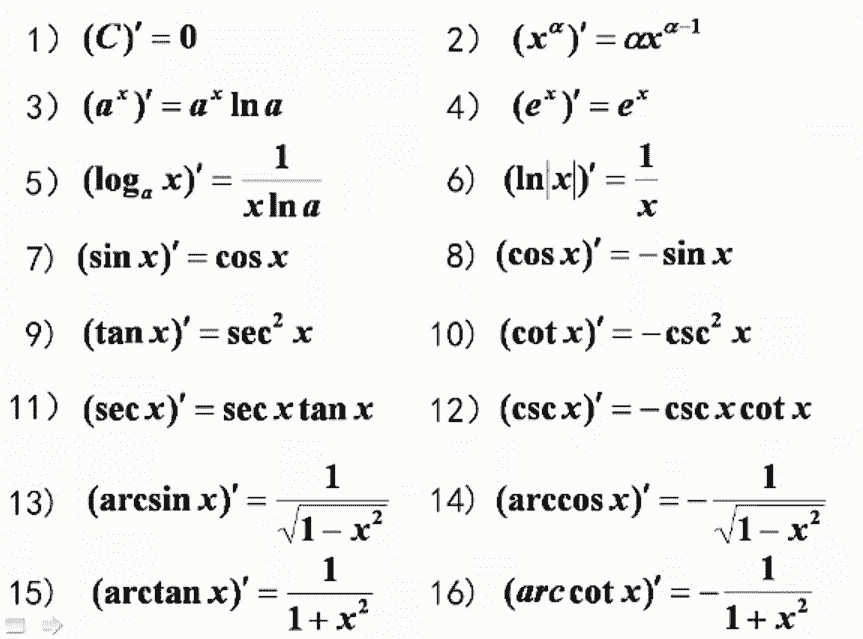
隐函数求导法

反函数的导数

高阶导数
常用的高阶导数公式
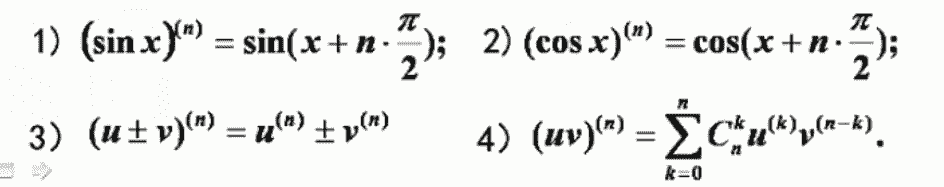
高阶导数求导方法:
- 直接使用公式
- 求一阶导数,二阶导数…归纳规律
第三章 微分中值定理及导数应用
微分中值定理
费马引理、罗尔定理

拉格朗日中值定理
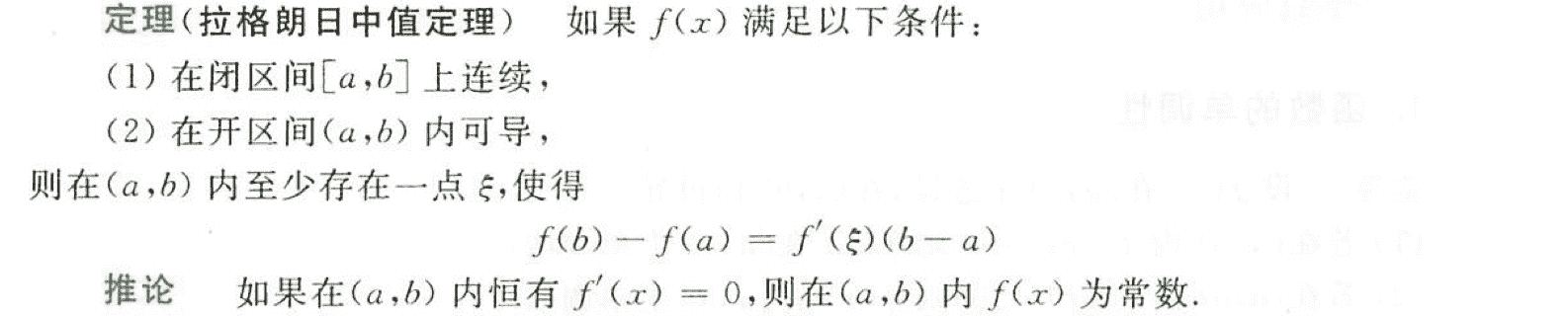
拉格朗日中值定理几何意义:曲线上至少有一点的切线,和连接两端点的弦是平行的。
柯西中值定理

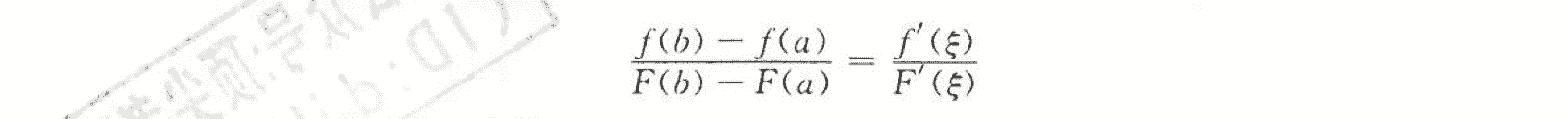
微分中值定理的关系
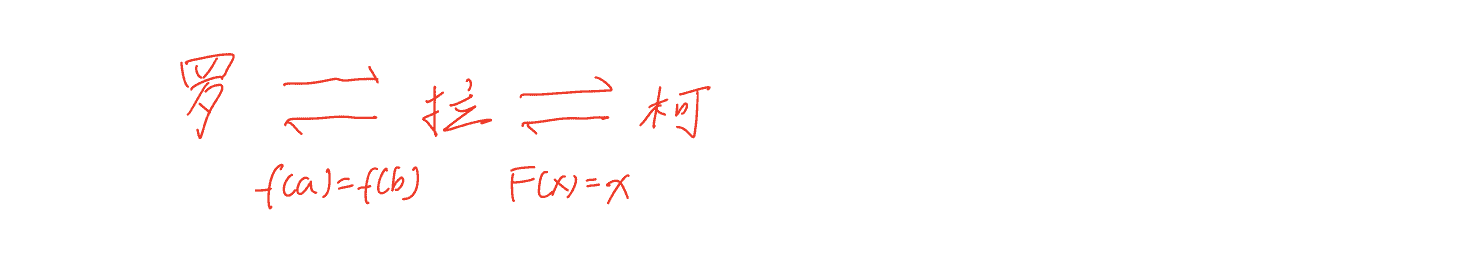
微分中值定理的本质都是用来建立导数和函数之间的联系。当题目给我们导数的条件,让我们研究函数,或者相反。我们就应该想到使用微分中值定理。
上面四个定理都是用来建立一阶导数和函数之间的关系,当我们需要建立高阶导数与函数之间的关系时,往往使用泰勒公式。
泰勒公式


泰勒展开式的意义
- 建立f(x)和高阶导数的关系·
- 用多项式来逼近f(x)。因为多项式求极限、导数和积分都很简单。
皮亚诺余项和拉格朗日余项的比较
-
皮亚诺余项称为(局部泰勒公式)。因为只能保证误差在$x$充分靠近$x_0$ 的时候比较小。
-
拉格朗日余项(整体)。在n趋向无穷的时候在一个大的范围内都是趋向于0的。
-
皮亚诺余项-局部性态-极限、极值
-
拉格朗日余项-整体性态-最值、不等式
常用的泰勒公式
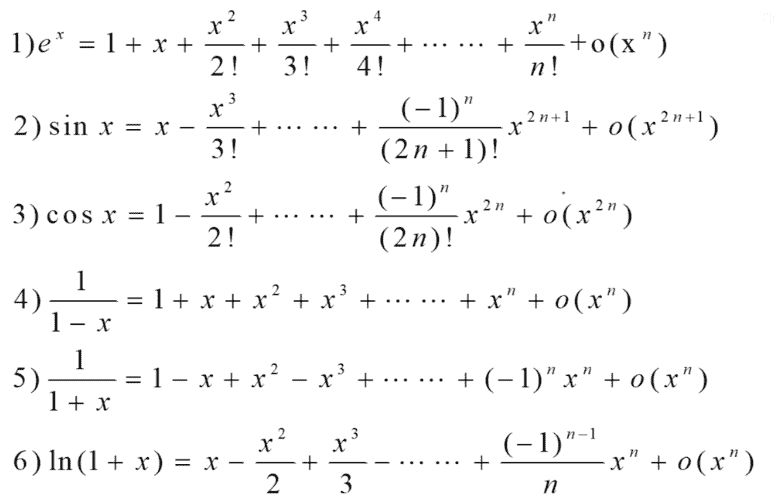
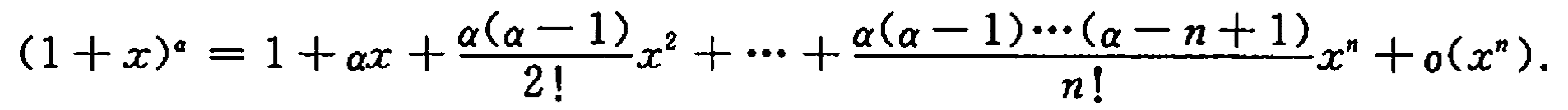
泰勒公式记忆方法

其他几个泰勒展开式可以通过等价代换推导
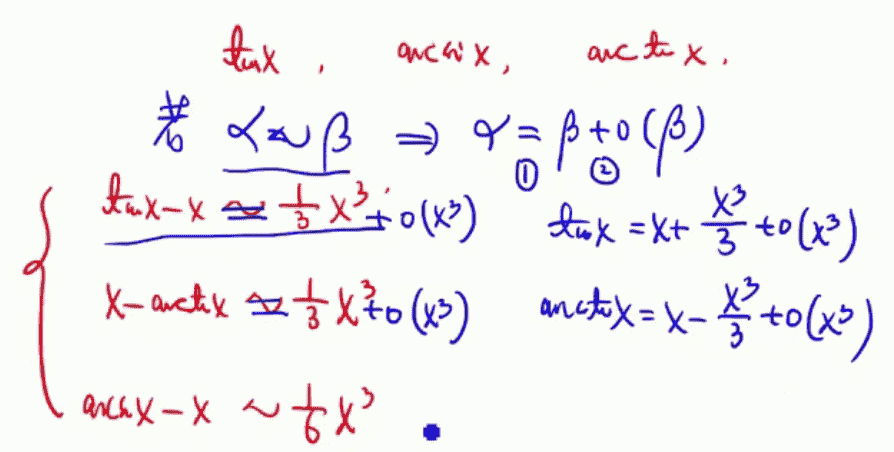
导数应用
极值


最值(最大值、最小值)

曲线的凹凸性

拐点


渐近线

快速判断、找到斜渐近线
首先几何上理解渐近线:
曲线上的一个动点,沿着曲线趋向于无穷远时,这个点到直线之间的距离,记作d。如果距离d趋向0,那么这条直线就叫做曲线的渐近线。
如果这条直线是水平的,那就是水平渐近线。如果直线是垂直的,就是垂直渐近线。如果直线是斜的,那就是斜渐近线。
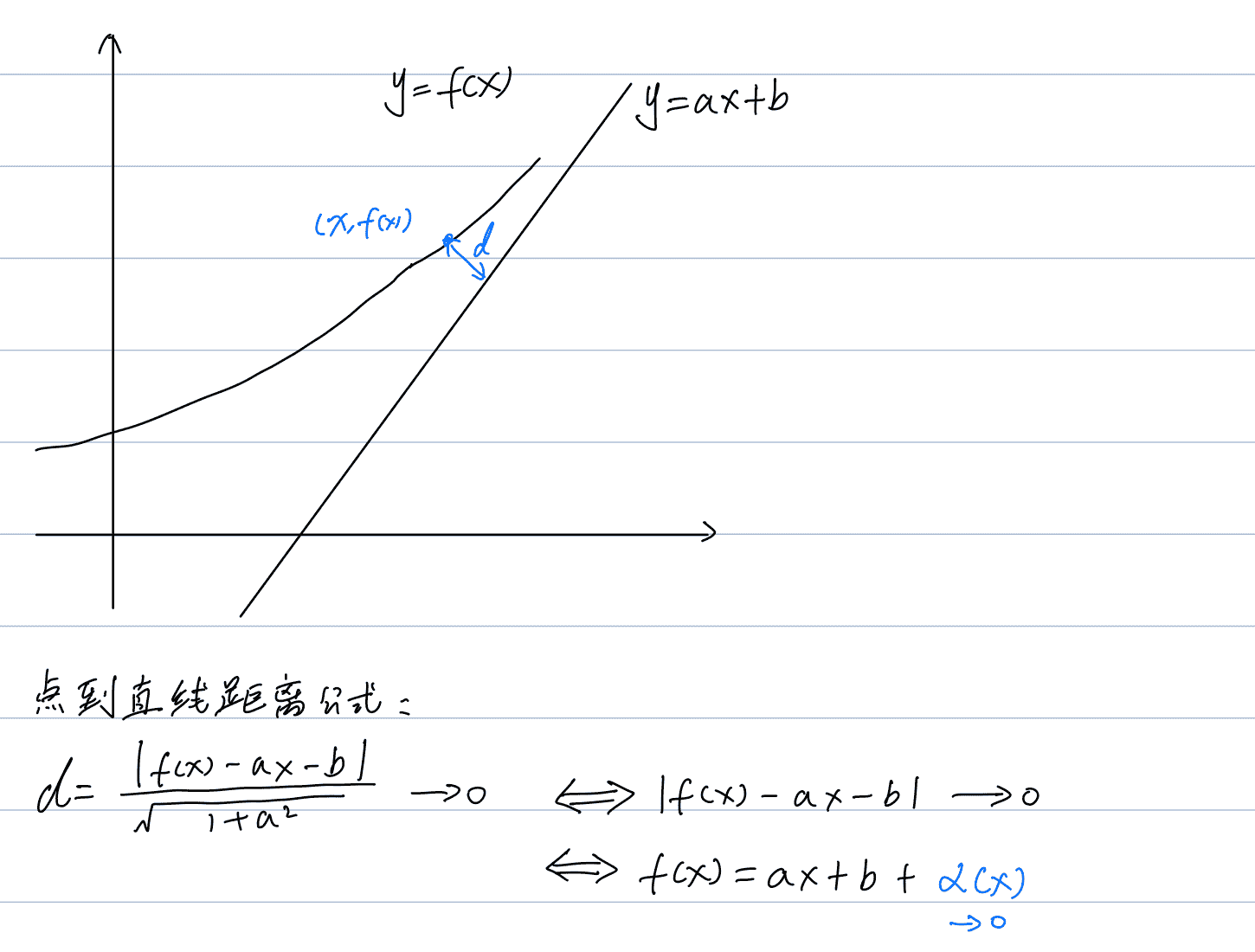
如果一个曲线能够写成一个线性函数(ax+b)加上趋向0的数的形式。那么这个曲线就有斜渐近线,且那个线性函数就是该曲线的斜渐近线。
方程的根(证明)

不等式的证明

常用不等式、基本不等式、经典不等式
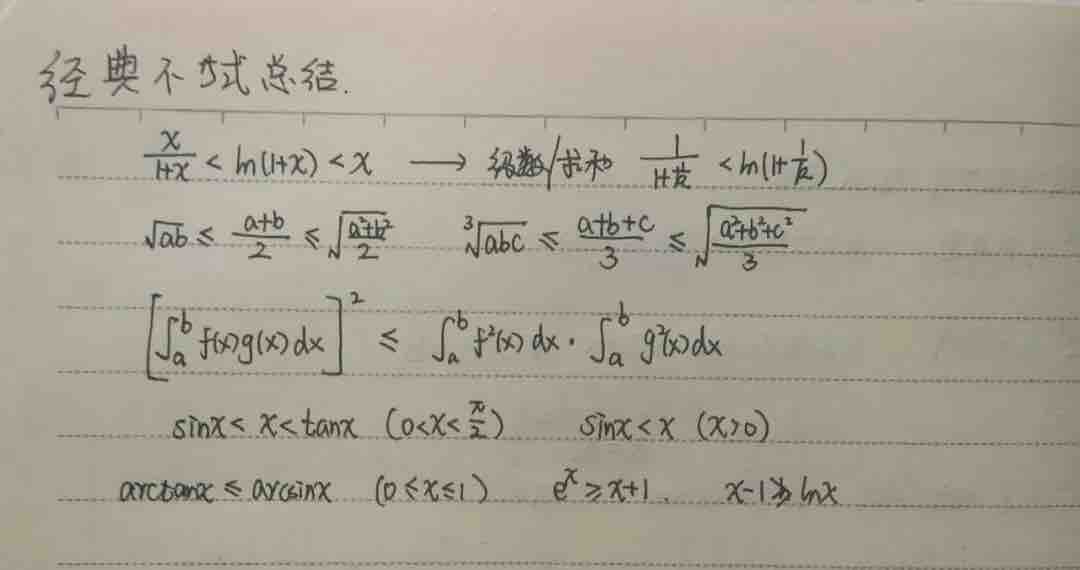
中值定理证明题
第四章 不定积分
不定积分的概念与性质
原函数存在定理

不定积分的性质
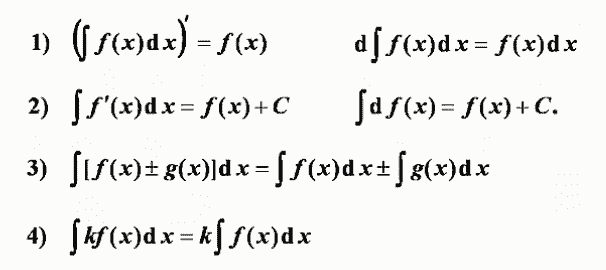
不定积分基本公式

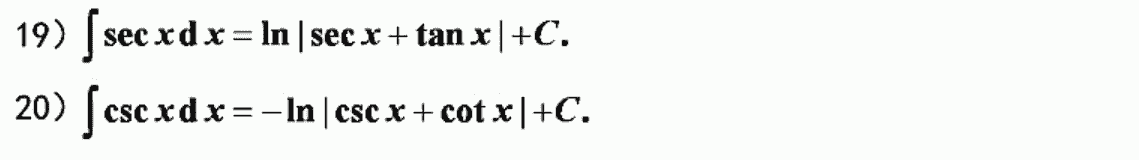
三种主要积分法
第一换元积分法(凑微分法)
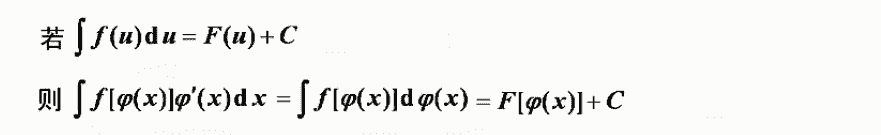
常见的凑非分形式: 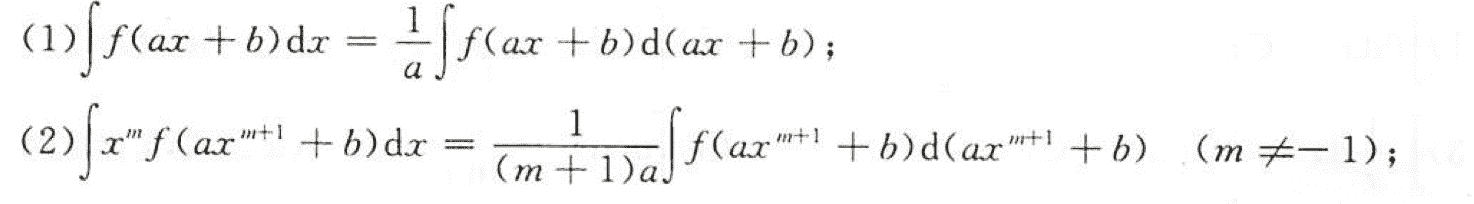
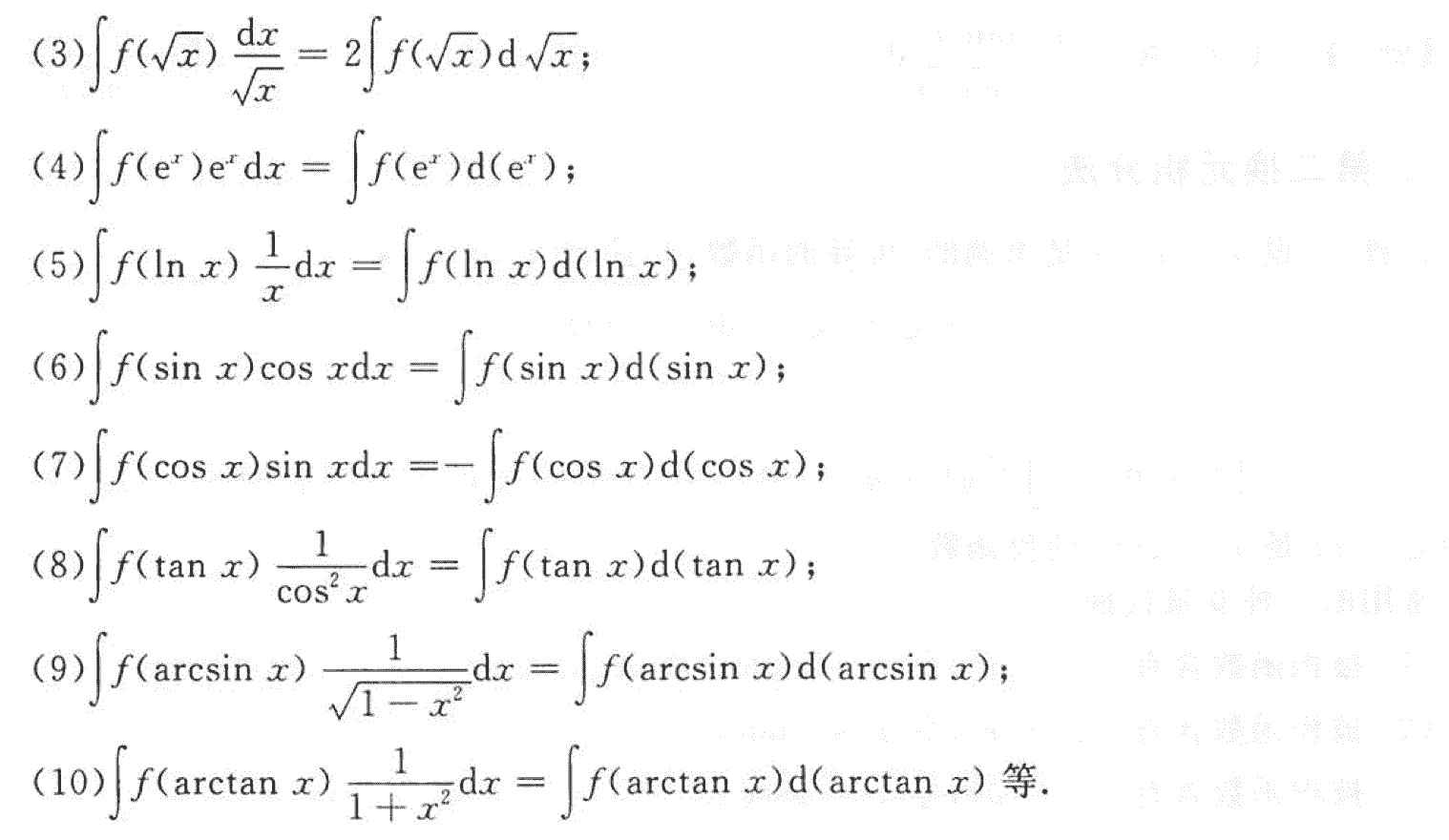
(3)很常用
第二换元积分法(三角代换去根号 )

分部积分法

三个常用的积不出的积分
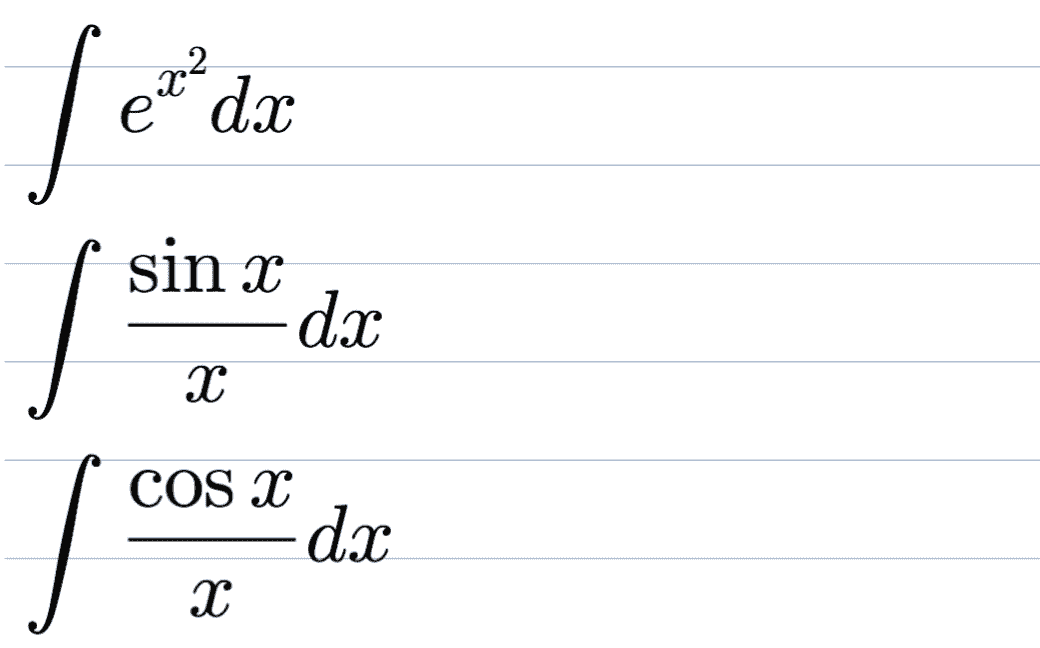
三类常见可积函数积分
有理函数积分

部分分式法:把分母分解因式分解到不能再分解,然后进行拆项,(这里可以通过初等数学里拆项裂项技巧进行操作)然后逐个积分。考试中该方法用得很少,基本都是特殊方法
三角有理式积分
三角有理式可以通过万能代换法,一定能做出来,但是运算量很大。尽量使用特殊方法。

一般三角函数次数比较低的积分适合用万能代换,如果方次高的话,代换完了,有理式的方次也很高,比较麻烦。
简单无理函数积分

对于此类函数积分,很少能找到简单方法,所以一般都是用这种一般方法。
第五章 定积分与反常积分
定积分的概念
定积分的性质
积分上限的函数
微积分第一基本定理
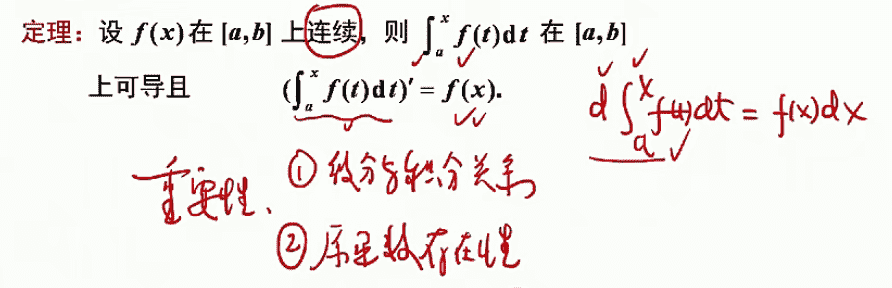
定理
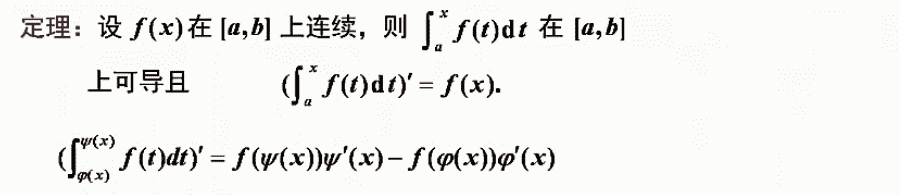
定积分的计算

利用已有公式(华氏公式)
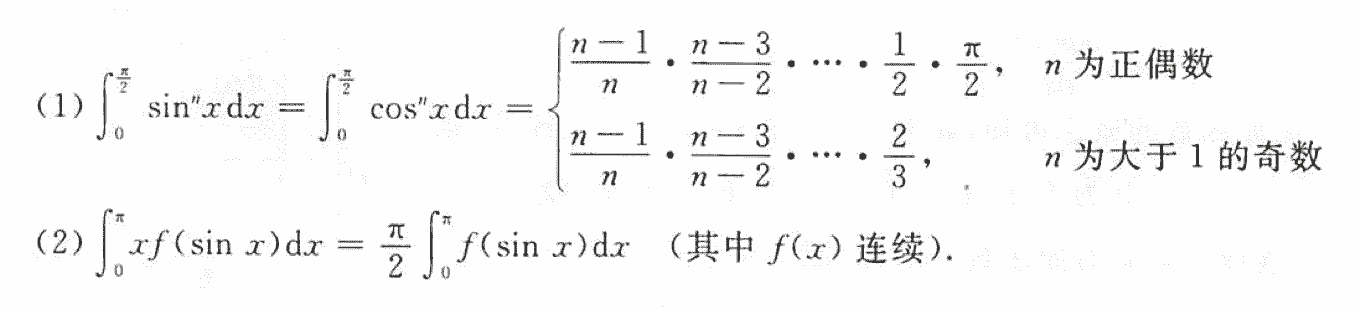

计算n项和极限时,如何判断使用夹逼原理还是定积分的定义
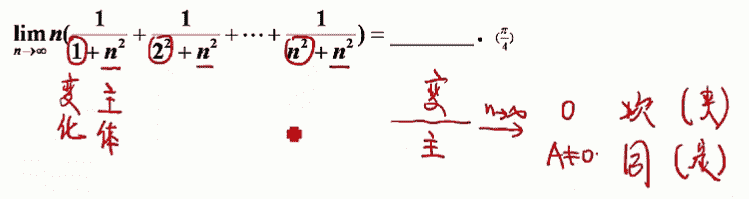
- 计算n项和极限时,需要首先判断n项中的变化部分和主体部分。
- 用变化部分比上主体部分,当n趋向于无穷大时,如果等于0,那么说明变化部分是主体部分的次量级,这时候用夹逼原理。如果二者之比为非零常数,那么说明是同量级,这时候用定积分的定义来计算(提1/n可爱因子)。
定积分几何意义算定积分的值
两个常用基本结论: 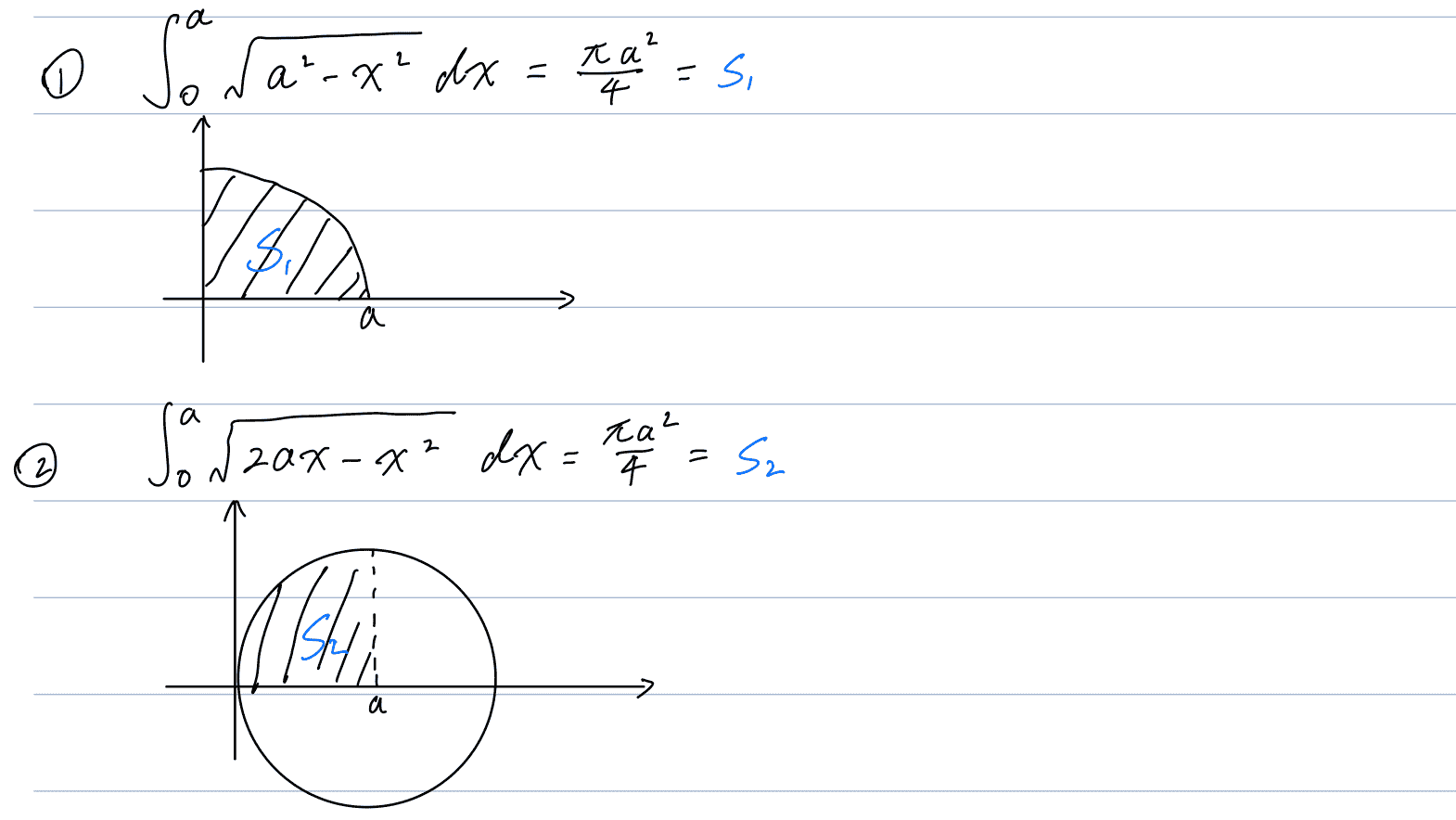
无穷区间上的反常积分

上述极限存在,则称反常积分收敛;反之,则称其发散。
常用结论(p积分)

无界函数的反常积分

常用结论(p积分)

常考题型:
- 反常积分的敛散性(使用定义,使用p积分)
- 反常积分的计算
第六章 定积分的应用
几何应用
平面图形的面积

这两个公式可以算,或者可以直接对1做个二重积分,也能算出来面积。
旋转体体积
该公式可以用,但下面有更一般方法。 
-
环绕x轴旋转: 竖带绕着x轴旋转,形成一个以x轴为圆心的薄原片,然后再从a到b积分。
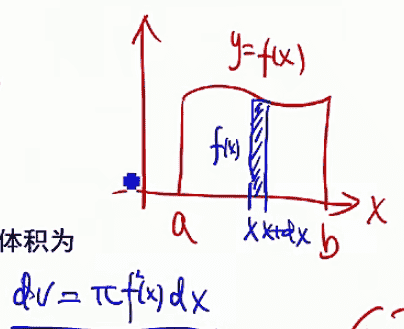
-
环绕y轴旋转: 竖带绕着y轴旋转,形成薄圆筒,把这个圆筒从某处截断,展开成一个长方体。长方体的长度就是圆筒的周长2*pi *x;长方体的截面积等于高度f(x)c乘以宽度dx。

注意:上面的方法可以用,但是同样的,能够有更加一般、简单的方法来处理这一类题目。
可以使用二重积分来解决这类问题。 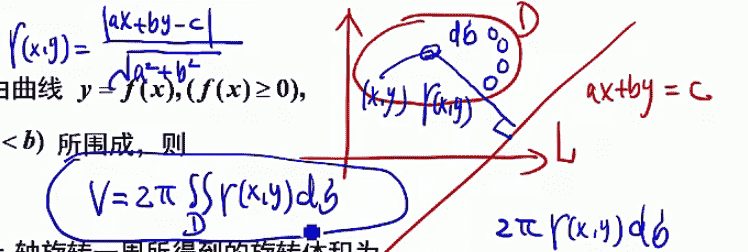
第七章 微分方程
常微分方程的基本概念
一阶微分方程
可分离变量的方程
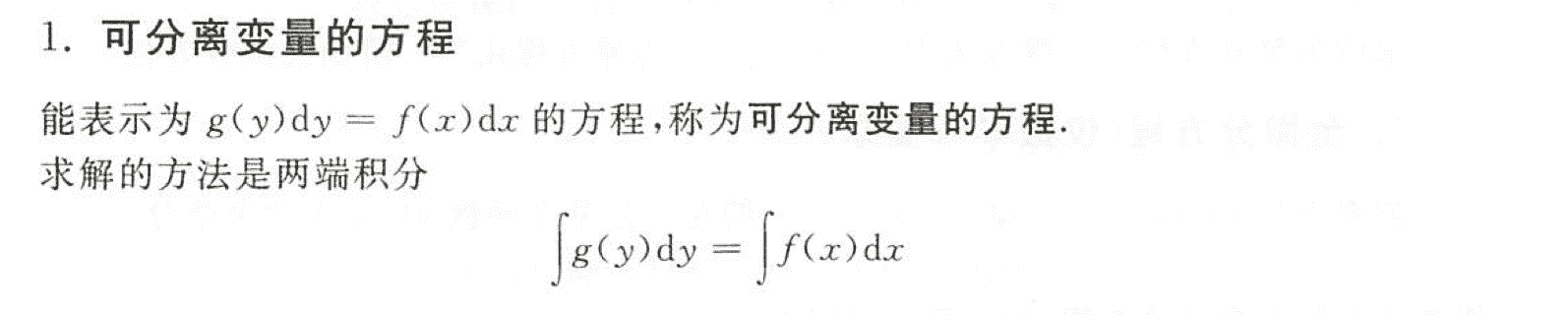
齐次微分方程

一阶线性微分方程
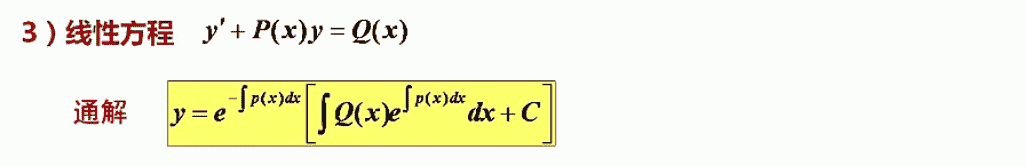
注意:只要加最后面一个常数C,前面的积分都不用加常数,而且前面积分积出来ln(x)都不用加绝对值。
高阶线性微分方程

方程(1)的两个解线性无关的充要条件是它们之比不为常数。

常系数齐次线性微分方程

虽然这个方法是用于二阶微分方程,但是三阶乃至于更高阶其实都适用。比如三阶方程解出来三个根,那么把这些根所对应的解加起来就能得到三阶微分方程的解。
### 常系数非齐次线性微分方程 

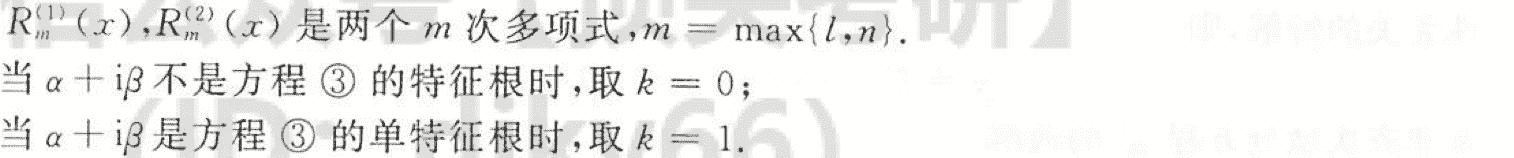
差分方程

第八章 多元函数微分学
多元函数的极限
多元函数的连续性
偏导数
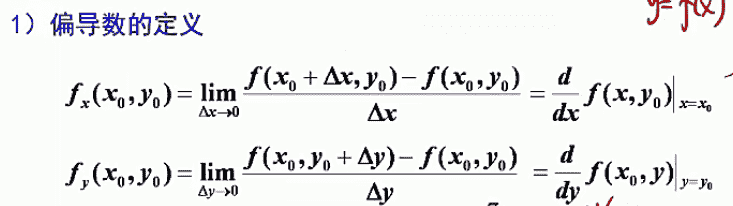
高阶偏导数

全微分


连续、可偏导及可微之间的关系
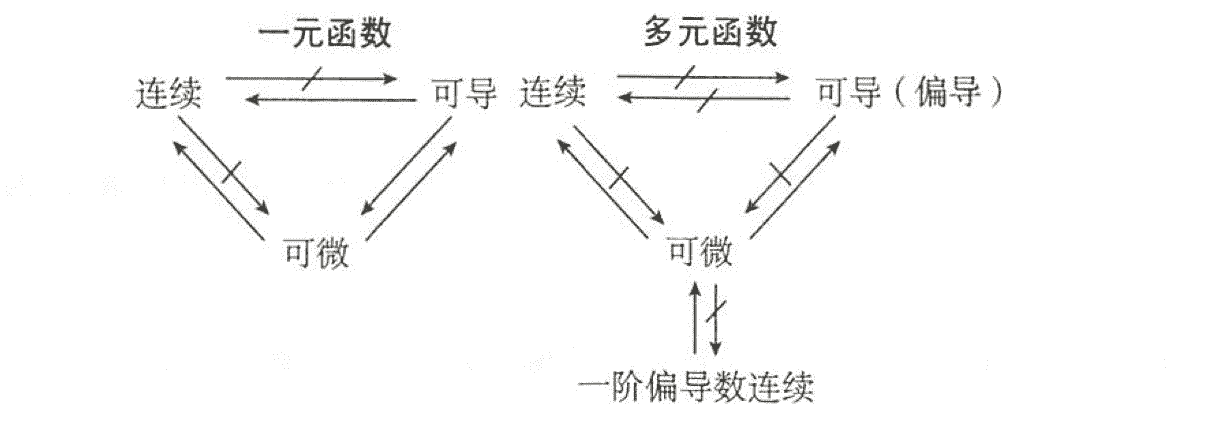
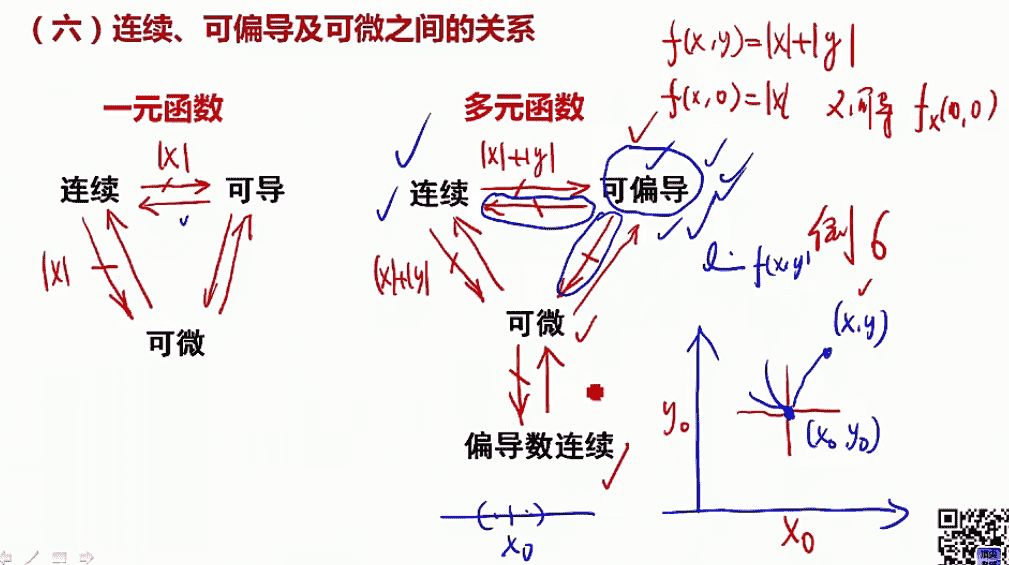
复合函数微分法

全微分形式的不变性
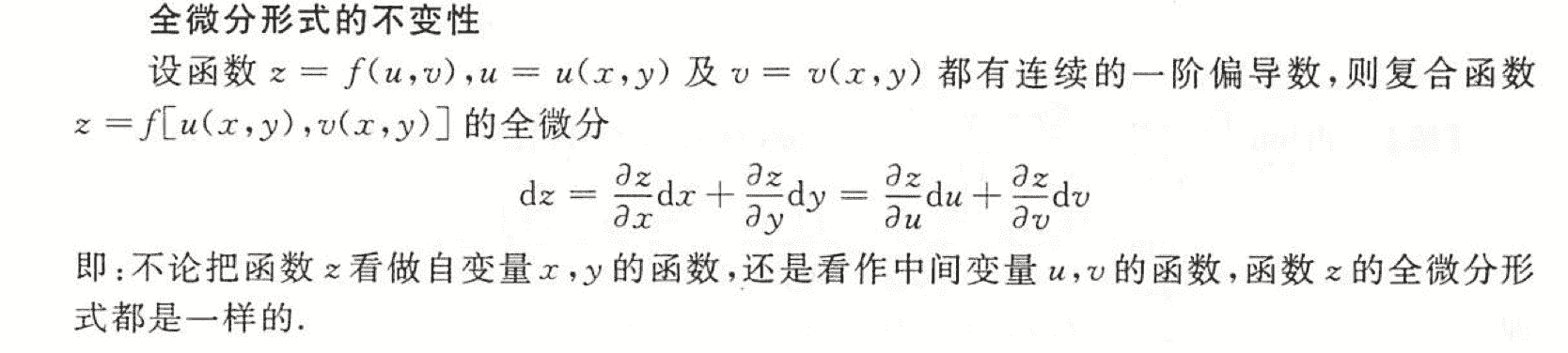
隐函数微分法

求偏微分的两种方法
- 直接对于给定的公式两端对x求偏导,整理得出z对x的偏导。z对y的偏导同理。注意:在使用此方法时,把z作为x,y的函数并进行求导。
- 使用上述公式求偏微分。注意:当对大F求x的偏导时,要把z当做常数来处理,千万不要当做函数继续求导!!!
- 利用微分形式不变性。把dz用dx和dy表达出来。
无约束极值


条件极值及拉格朗日乘数法

最大值、最小值
略
第九章 二重积分
二重积分的概念及性质



二重积分的计算
利用直角坐标计算
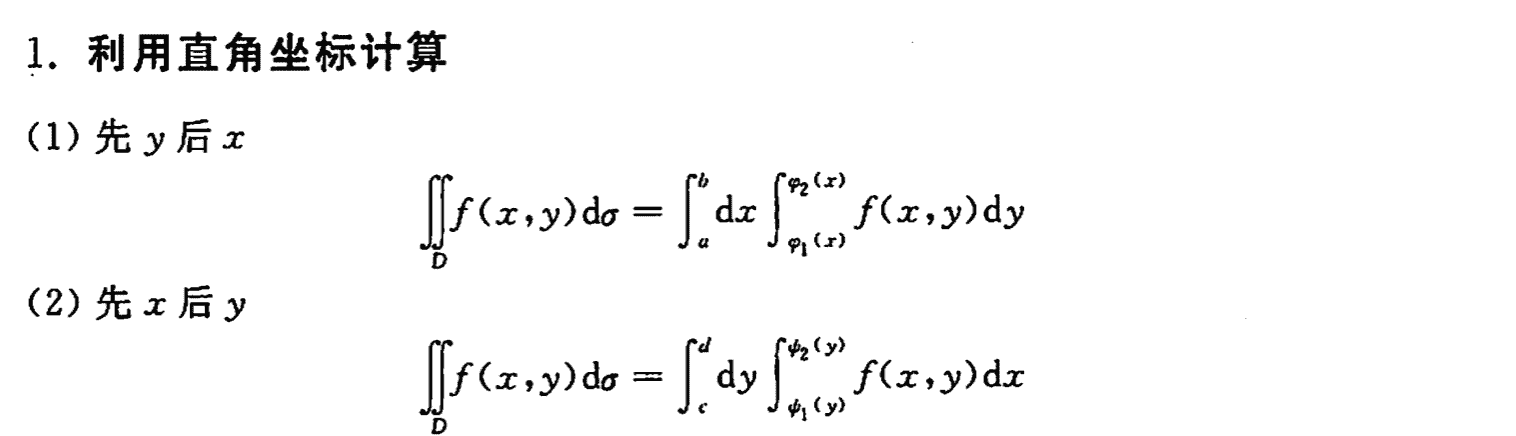
利用极坐标计算

利用函数的奇偶性计算

利用变量的轮换对称性计算
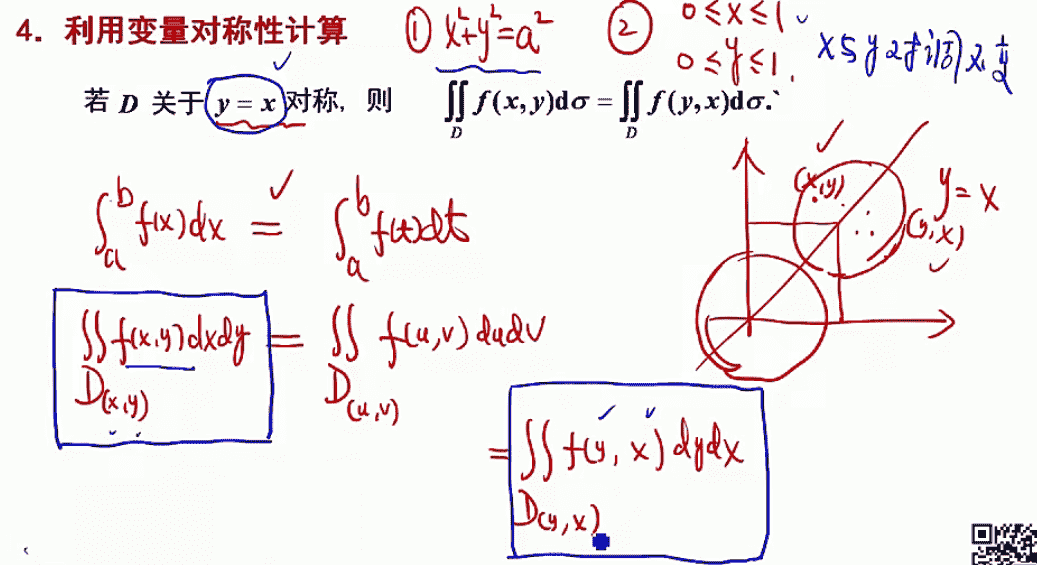
第十章 无穷级数
常数项级数


级数的审敛准则
正向级数



交错级数

任意项级数

幂级数


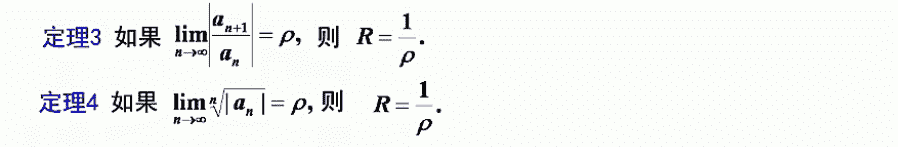 注意:
注意:
当遇到缺项的幂级数的时候,不能直接用上面的这个公式,计算方法如下: 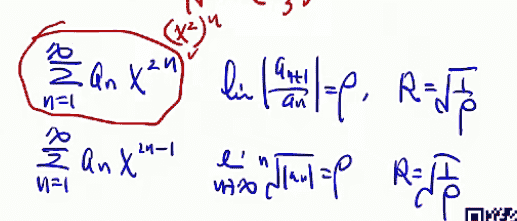
幂级数的性质


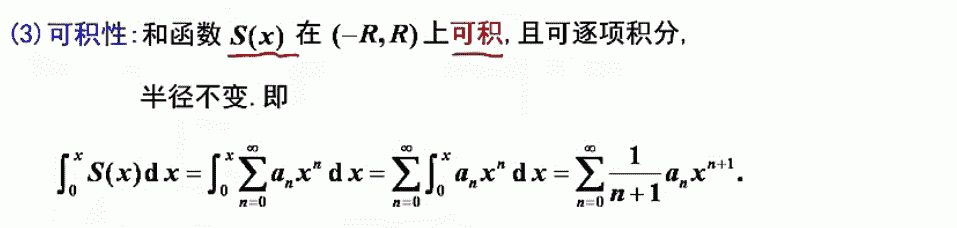
函数的幂级数展开


几个常用的展开式