Algorithm --> 十大排序算法

十大排序算法

 

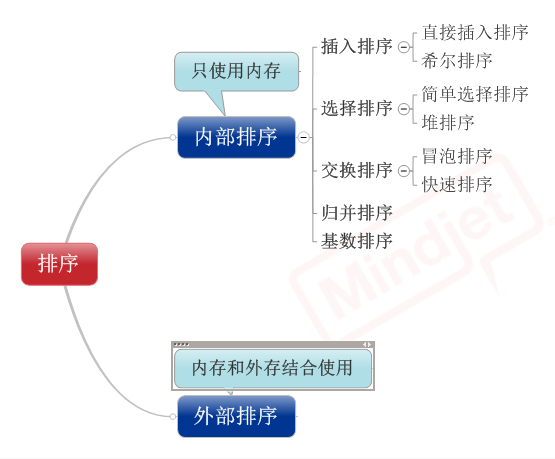
主要排序法有：  
一、冒泡（ Bubble）排序—— 相邻交换  
二、选择排序 ——每次最小/ 大排在相应的位置  
三、插入排序 ——将下一个插入已排好的序列中  
四、壳（ Shell）排序—— 缩小增量  
五、归并排序  
六、快速排序  (待补充)
七、堆排序  (待补充)
八、拓扑排序  (待补充)
九、锦标赛排序  (待补充)
十、基数排序  (待补充)

 

 

1、冒泡（ Bubble）排序 

基本思想：在要排序的一组数中，对当前还未排好序的范围内的全部数，自上而下对相邻的两个数依次进行比较和调整，让较大的数往下沉，较小的往上冒。即：每当两相邻的数比较后发现它们的排序与排序要求相反时，就将它们互换。

void BubbleSortArray() 
{ 
    for(int i=1;i<n;i++) 
    { 
        for(int j=0;i<n-i;j++) 
        { 
            if(a[j]>a[j+1])//比较交换相邻元素 
            { 
                int temp; 
                temp=a[j];
                a[j]=a[j+1];
                a[j+1]=temp; 
            } 
        } 
    } 
} 

效率 O（ n²）, 适用于排序小列表。

 

2、选择排序

基本思想：在要排序的一组数中，选出最小的一个数与第一个位置的数交换；然后在剩下的数当中再找最小的与第二个位置的数交换，如此循环到倒数第二个数和最后一个数比较为止。

void SelectSortArray() 
{ 
    int min_index; 
    for(int i=0;i<n-1;i++) 
    { 
        min_index=i; 
        for(int j=i+1;j<n;j++)//每次扫描选择最小项 
        {
              if(arr[j]<arr[min_index])  
                min_index=j;
        } 
        if(min_index!=i)//找到最小项交换，即将这一项移到列表中的正确位置  
        { 
            int temp; 
            temp=arr[i];
            arr[i]=arr[min_index];
            arr[min_index]=temp; 
        } 
    } 
} 

效率O（ n²），适用于排序小的列表。

 

 

3、 插入排序

基本思想：在要排序的一组数中，假设前面(n-1) [n>=2] 个数已经是排好顺序的，现在要把第n个数插到前面的有序数中，使得这n个数也是排好顺序的。如此反复循环，直到全部排好顺序。

void InsertSortArray() 
{ 
    for(int i=1;i<n;i++)//循环从第二个数组元素开始，因为 arr[0]作为最初已排序部分 
    { 
        int temp=arr[i];//temp标记为未排序第一个元素  
        int j=i-1; 
        while (j>=0 && arr[j]>temp)/*将 temp与已排序元素从小到大比较，寻找 temp应插入的位置*/ 
        { 
            arr[j+1]=arr[j]; 
            j--; 
        } 
        arr[j+1]=temp; 
    } 
} 

最佳效率 O（n ）；最糟效率 O（n² ）与冒泡、选择相同，适用于排序小列表，若列表基本有序，则插入排序比冒泡、选择更有效率。

 

4、希尔（Shell）排序

基本思想：算法先将要排序的一组数按某个增量d（n/2,n为要排序数的个数）分成若干组，每组中记录的下标相差d.对每组中全部元素进行直接插入排序，然后再用一个较小的增量（d/2）对它进行分组，在每组中再进行直接插入排序。当增量减到1时，进行直接插入排序后，排序完成。

void  ShellSortArray1() 
{ 
    for(int incr=3;incr>0;incr--)//增量递减，以增量 3，2 ，1为例  
    { 
        for(int L=0;L<(n-1)/incr;L++)//重复分成的每个子列表 
        { 
            for(int i=L+incr;i<n;i+=incr)//对每个子列表应用插入排序  
            { 
                int temp=arr[i]; 
                int j=i-incr; 
                while(j>=0&&arr[j]>temp) 
                { 
                    arr[j+incr]=arr[j]; 
                    j-=incr; 
                } 
                arr[j+incr]=temp; 
            } 
        } 
    } 
} 

void  ShellSortArray2(int *data, int len) 
{ 
    int d = len;
    while(d > 1)
    {
        d = (d+1)/2;
        for(int i=0; i<len-d; i++)
        {
            if(data[i+d] < data[i])
            {
                int tmp = data[i+d];
                data[i+d] = data[i];
                data[i] = tmp;
            }
        }
    }
} 

适用于排序小列表。 效率估计 O（nlog2^n ）~O（ n^1.5），取决于增量值的最初大小。建议使用质数作为增量值，因为如果增量值是 2的幂，则在下一个通道中会再次比较相同的元素。 壳（Shell）排序改进了插入排序，减少了比较的次数。是不稳定的排序，因为排序过程中元素可能会前后跳跃。  

 

5、归并排序

基本思想：归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

//将有二个有序数列a[first...mid]和a[mid...last]合并。  
void mergearray(int a[], int first, int mid, int last, int temp[])  
{  
    int i = first, j = mid + 1;  
    int m = mid,   n = last;  
    int k = 0;  
      
    while (i <= m && j <= n)  
    {  
        if (a[i] <= a[j])  
            temp[k++] = a[i++];  
        else  
            temp[k++] = a[j++];  
    }  
    while (i <= m)  temp[k++] = a[i++];  
    while (j <= n)  temp[k++] = a[j++];  
    for (i = 0; i < k; i++)  
        a[first + i] = temp[i];  
} 

void mergesort(int a[], int first, int last, int temp[])  
{  
    if (first < last)  
    {  
        int mid = (first + last) / 2;  
        mergesort(a, first, mid, temp);    //左边有序  
        mergesort(a, mid + 1, last, temp); //右边有序  
        mergearray(a, first, mid, last, temp); //再将二个有序数列合并  
    }  
}  
  
bool MergeSort(int a[], int n)  
{  
    int *p = new int[n];  
    if (p == NULL)  return false;  
    mergesort(a, 0, n - 1, p);  
    delete[] p;  
    return true;  
}