[leetcode] N-Queens

 

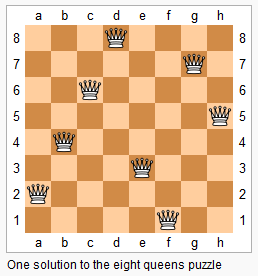
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens' placement, where'Q'and'.'both indicate a queen and an empty space respectively.

For example,
There exist two distinct solutions to the 4-queens puzzle:

[
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

 

https://oj.leetcode.com/problems/n-queens/

思 路：经典的8皇后问题，还是老思路，生成perm数组，perm[i]的只代表第i行放置皇后的列数，递归下去的条件是不冲突（冲突的情 况：perm[j] == i || perm[j] - j == i - cur || perm[j] + j == i + cur），然后根据题目要求生成结果的形式即可。

import java.util.ArrayList;

public class Solution {
    public ArrayList<String[]> solveNQueens(int n) {
        if (n <= 0)
            return null;
        ArrayList<String[]> res = new ArrayList<String[]>();
        int[] perm = new int[n];
        slove(perm, 0, n, res);

        return res;
    }

    private void slove(int[] perm, int cur, int n, ArrayList<String[]> res) {
        if (cur == n) {
            String[] tmp = new String[n];
            for (int i = 0; i < n; i++) {
                char[] item = new char[n];
                for (int j = 0; j < n; j++)
                    item[j] = '.';
                item[perm[i]] = 'Q';
                tmp[i] = new String(item);
            }
//          System.out.println(Arrays.toString(tmp));
            res.add(tmp);

        } else {
            int i;
            for (i = 0; i < n; i++) {
                int j;
                boolean ok = true;
                for (j = 0; j < cur; j++) {
                    if (perm[j] == i || perm[j] - j == i - cur
                            || perm[j] + j == i + cur)
                        ok = false;
                }
                if (ok) {
                    perm[cur] = i;
                    slove(perm, cur + 1, n, res);
                }

            }

        }

    }

    public static void main(String[] args) {
        System.out.println(new Solution().solveNQueens(4));

    }
}

 

第三遍记录：

import java.util.ArrayList;

public class Solution {
    public ArrayList<String[]> solveNQueens(int n) {
        if (n <= 0)
            return null;
        ArrayList<String[]> res = new ArrayList<String[]>();
        int[] perm = new int[n];
        solve(perm, 0, n, res);

        return res;
    }
    
    private void solve(int[]perm,int cur,int n,ArrayList<String[]> res){
        if(cur==n){
            String[] tmp = generateRes(perm);
            res.add(tmp);
            return;
        }
        for(int i=0;i<n;i++){
            boolean ok =true;
            
            // check the conflict with perm[cur]=i
            // j perm[j], cur i
            for(int j=0;j<cur;j++){
                if(perm[j]==i||perm[j]-j==i-cur||perm[j]+j==i+cur){
                    ok=false;
                    break;   
                }
                
            }
            
            if(ok){
                perm[cur]=i;
                solve(perm,cur+1,n,res);
            }
            
        }
    
    }
    
    private String[] generateRes(int[] perm){
        String[] res = new String[perm.length];
        
        for(int i=0;i<res.length;i++){
            StringBuilder sb = new StringBuilder();
            for(int j=0;j<res.length;j++){
                if(perm[i]==j)
                    sb.append("Q");
                else
                    sb.append(".");
            }               
            res[i] = sb.toString();
            
        }
        
        return res;
        
    }

}