[leetcode] Search for a Range

Given a sorted array of integers, find the starting and ending position of a given target value.

Your algorithm's runtime complexity must be in the order of O(log n).

If the target is not found in the array, return[-1, -1].

For example,
Given[5, 7, 7, 8, 8, 10]and target value 8,
return[3, 4].

https://oj.leetcode.com/problems/search-for-a-range/

排过序的数组，要求时间是logn，一看就是要用binary search。 值得一读， 值得一读2

思路1：binary search到元素，然后向两边扩展找相同元素，最坏情况O(n).

思路2：对binary search稍微修改，然后进行两次binary search，分别定位指定元素的下界和上界。

思路2代码：

已删除

 第二遍记录：

　　两个函数的名字改一下分别叫：lowerBound 和 upperBound。

public class Solution {
    public int[] searchRange(int[] A, int target) {
        if (A == null || A.length == 0)
            return new int[] { -1, -1 };
        int n = A.length;
        int floor = lowerBound(A, target);
        int ceiling = upperBound(A, target);
        if (ceiling > floor)
            return new int[] { floor, ceiling - 1 };

        else
            return new int[] { -1, -1 };
    }

    public int lowerBound(int[] a, int x) {
        int left = 0;
        int right = a.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (x > a[mid]) {
                left = mid + 1;
            } else if (x <= a[mid]) {
                right = mid - 1;
            }
        }
        return left;
    }

    public int upperBound(int[] a, int x) {
        int left = 0;
        int right = a.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (x >= a[mid]) {
                left = mid + 1;
            } else if (x < a[mid]) {
                right = mid - 1;
            }
        }
        return left;
    }

}

 

第N遍，

分析为什么left是最终需要的坐标，考虑最后left和right相交的两种情况（lrm都在最后一个元素，lrm在最后两个元素），分情况讨论。

 

 

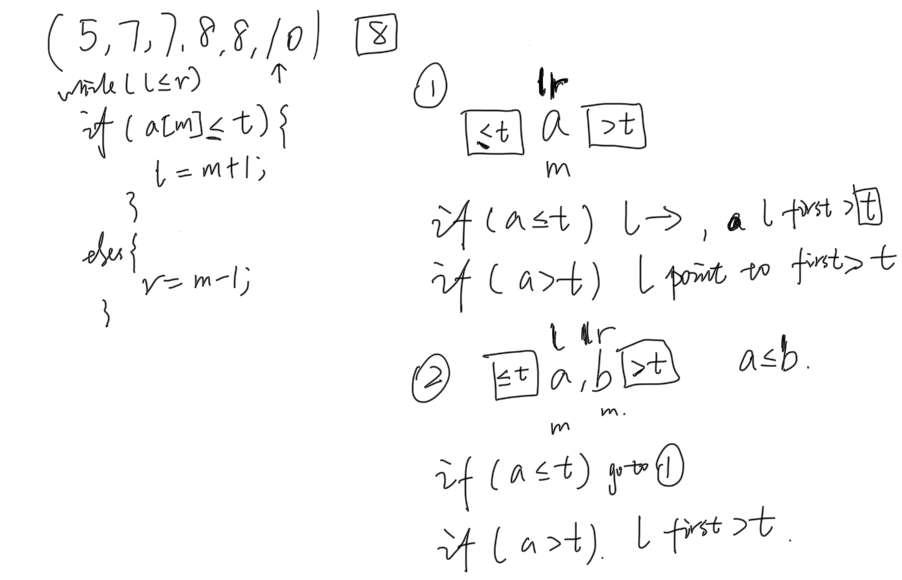
第n遍，尝试使用binary search template 2， 注意upperbound对于大于所有数组元素的target需要返回长度加一的index，所以 r = nums.length instead of r = nums.length-1;

class Solution {
    public int[] searchRange(int[] nums, int target) {
        if(nums == null || nums.length == 0){
            return new int[]{-1,-1};
        }
        int lowerBound = lowerBound(nums,target);
        if(lowerBound == -1){
            return new int[]{-1,-1};
        }
        int upperBound = upperBound(nums,target);
        return new int[]{lowerBound, upperBound-1};
        
    }
    
    private int lowerBound(int[] nums, int target){
        int l = 0, r = nums.length-1;
        
        while(l<r){
            int mid = l + (r-l)/2;
            if(nums[mid]>=target){
                r = mid;
            }else{
                l = mid+1;
            }
        }
        return nums[l]==target?l:-1;
    }
    
    private int upperBound(int[] nums, int target){
        int l =0, r = nums.length;
        
        while(l<r){
            int mid = l + (r-l)/2;
            if(nums[mid]<=target){
                l = mid+1;
            }else{
                r = mid;
            }
        }
        return l;
    }
    
}